Laboratoryjne zajęcie N9

Model regresji liniowej wielu zmiennych (2 god.)

1. Estymacja parametrów modelu

2. Ekonometryczna analiza produkcji: model liniowy

Metoda najmniejszych kwadratów.

Załóżmy, że celem badania jest zmienna objaśniana Y, która zależy od zmiennych objaśniających X₁, X₂, … X_K. Załóżmy, że dane statystyczne, dotyczące tych zmiennych, zgromadzone w macierze

[Y|X] =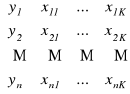
= [y_(i) |X].

Definicja Modelem regresji liniowej wielu zmiennych nazywa się ekonometryczny model postaci

y_i = a₁x_i1 + a₂x_i2 + … + a_Kx_iK + ξ_i, i = 1, 2, …, n.

Wartości x_ik, k = 1, 2, …, K, zmiennych objaśniających X_k, k = 1, 2, …, K w powtarzalnych próbach i = 1, 2, …, n są ustalonymi liczbami rzeczywistymi, zatem elementy macierzy X są nielosowe.

Składnik losowy ξ_i modelu jest zmienną losową o rozkładzie normalnym. Rozkład ξ_i nie zależy od numeru i kolejnej obserwacji (i = 1, 2, …, n) i jest rozkładem normalnym o parametrach (0, σ²):

ξ_i ⇔ N(0, σ²),

Eξ_i = 0, Dξ_i = σ², i = 1, 2, …, n.

Nie występuje autokorelacja składnika losowego, tj. zmienne losowe ξ_i dla różnych i = 1, 2, …, n są nieskorelowane:

Cov(ξ_i, ξ_j) = 0, i ≠ j, j, i = 1, 2,…, n

W postaci wektorowej stosowany jest zapis:

y_(i) = X⋅a_(k) + ξ_(i),

gdzie a_(k) jest wektorem parametrów strukturalnych modelu; y_(i) jest wektorem wszystkich n obserwacji zmiennej objaśnianej Y; X jest macierzą wszystkich obserwacji, dla wszystkich zmiennych objaśniających; ξ_(i) jest wektorem wartości składnika losowego dla wszystkich n obserwacji.

Wektor a*_(k) MNK - estymatorów wektora a_(k) parametrów strukturalnych modelu określa się według wzoru:

a*_(k) = (X^T⋅X)^-1⋅X^T⋅y_(i).

Wartości teoretyczne y*_(t) obliczamy według wzoru:

y*_(i) = Xa*_(k).

Wektor e_(i) reszt modelu określamy wzorem:

e_(i) = y_(i) - y*_(i).

Wartość σ*² nieobciążonego estymatora wariancji σ² składnika losowego oblicza się według wzoru:

=
,

natomiast wartość σ* estymatora odchylenia standardowego składnika losowego określamy wzorem:

.

Macierz D²(a*_(k)) wariancji-kowariancji wektora a*_(k) MNK - estymatorów parametrów strukturalnych modelu określa się wzorem:

D²(a*_(k)) = σ*²⋅ (X^T⋅X)^-1.

Zadania

Posiadamy dane liczbowe, dotyczące:

Q (w tys. zł) - wartość produkcji czystej;

K (w mln zł) - wartość brutto produkcyjnego majątku trwałego;

L (w osobach) - średnia liczba zatrudnionych w ciągu roku; a także o wartości.

Zakładając, że badany proces produkcyjny charakteryzuje się tym, że wydajność krańcowa względem poszczególnych czynników jest wartością stałą, zbudować odpowiedni model ekonometryczny dla funkcji produkcji Q.

Na podstawie merytorycznej analizy występujących w modelu zmiennych, biorąc pod uwagę przyjęte założenia, dochodzimy do wniosku, że właściwą postacią analityczną budowanego modelu będzie funkcja liniowa

q_t = a₀ + a_K⋅k_t + a_L⋅l_t + ⋅ξ_t, t = 1, 2, ..., n,

gdzie a_K, a_L są wartościami wydajności krańcowej względem poszczególnych czynników (K oraz L), a₀ jest wartością stałą.

1. Utworzyć macierz
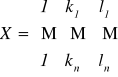
   i wstawić w skoroszyt. (<Wstaw> <Nazwa> <Definiuj> <Nazwa w skoroszycie>(...)<Odwołuje się do>:(...) <Dodaj> <OK>.).

2. Wstawić w skoroszyt wektor
   .

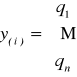
3. Oszacować parametry strukturalne modelu.

4. Obliczyć wartości teoretyczne y*_(i) modelu.

5. Obliczyć wektor e_(i) reszt modelu.

6. Oszacować parametry σ² (oraz σ) struktury stochastycznej modelu.

7. Obliczyć macierz D²(a*_(k)) wariancji-kowariancji wektora a*_(k) MNK - estymatorów parametrów strukturalnych modelu.

1

2

---