Laboratoryjne zajęcie N4

Model regresji liniowej jednej zmiennej

Metoda najmniejszych kwadratów

Modelem regresji liniowej jednej zmiennej nazywa się model postaci:

y_t = b + ax_t + ξ_t., t = 1, 2, ..., n,

gdzie x_t - zmienna objaśniana modelu, y_t - zmienna objaśniająca modelu, ξ_t - składnik losowy;

a, b - parametry strukturalne modelu.

Składnik losowy ξ_t jest zmienną losową o rozkładzie normalnym o parametrach (0, σ²):

ξ ≈ N(0,σ²).

Parametr σ²określa wariancję składnika losowego i nazywa się parametrem struktury stochastycznej modelu:

σ² = Dξ = E(ξ - Eξ)².

1. Estymacja punktowa parametrów strukturalnych modelu

Estymatory Metody Najmniejszych Kwadratów (MNK-estymatory) określamy z założenia, że suma kwadratów reszt jest najmniejsza, tzn.

→ min,

gdzie y*_t - wartości teoretyczne modelu, określane wzorem:

y*_t = b* + a*x_t, t = 1, 2, ..., n.

Różnice

e_t = y_t - y*_t, t = 1, 2, ..., n.

nazywają się resztami modelu

Wartości a*, b* MNK-estymatorów parametrów strukturalnych modelu obliczamy według wzorów:

;

,

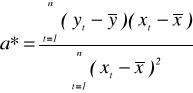
gdzie
- średnia arytmetyczna zmiennej X (
),

- średnia arytmetyczna zmiennej Y (
).

2. Estymacja parametru struktury stochastycznej modelu

Nieobciążony estymatora wariancji składnika losowego określa się wzorem:

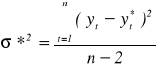
Estymator wariancji S²(a) estymatora a*, tzn.

S²(a) = D(a*) = E(a* - a)²

określa się wzorem:

,

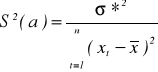
- odchylenie standardowe estymatora a*.

Estymator wariancji S²(b) estymatora b*, tzn.

S²(b) = D(b*) = E(b* - b)²

określa się wzorem:

,

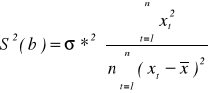
- odchylenie standardowe estymatora b*.

Współczynnik determinacji modelu R² określa się wzorem:

.

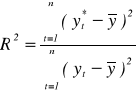
Zadania

1. Za pomocą funkcji „REGLINP” obliczyć wartości estymatorów (a*, b*) parametrów strukturalnych modelu.

2. Obliczyć wartości teoretyczne modelu y*_t według wzoru:

y*_t = b* + a*x_t, t = 1, 2, ..., n.

3. Obliczyć wartości teoretyczne modelu y*_t, stosując funkcję „REGLINW”.

4. Obliczyć wartości estymatorów σ*², σ*, S²(a), S(a), S²(b), S(b), oraz wartość R² współczynnika determinacji według wymienionych wyżej wzorów.

5. Obliczyć wartości estymatorów σ*, S(a), S(b), oraz wartość R² współczynnika determinacji stosując funkcję „REGLINP”..

1