Laboratoryjne zajęcie N7

Metody doboru postaci analitycznej modelu

Metoda heurystyczna

1. Współczynnik determinacji

2. Transformacja liniowa

3. Estymacja parametrów najczęściej spotykanych nieliniowych modeli ekonometrycznych

4. Metoda heurystyczna

Współczynnik determinacji R²

Całkowitą wariancją
zmiennej objaśnianej Y określa się równością:

,

gdzie y₁, y₂, ..., y_n - wartości empirycznych zmiennej objaśnianej Y,
- średnia arytmetyczna tych wartości.

Całkowitą wariancją
wartości teoretycznych
,
, ...,
, otrzymanych na podstawie zbudowanego modelu, określamy wzorem

.

jest skutkiem zmienności wartości zmiennej objaśniającej X i może być traktowana jako liczbowa miara tej części zmienności zmiennej objaśnianej Y, która jest formalnie przez model opisana, czyli jest zmiennością objaśnioną.

Współczynnikiem determinacj R² nazywamy stosunek:

.

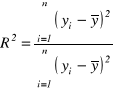
Wartości R² należą do przedziału liczbowego [0,1], oraz informuje on, jaką część całkowitej zmienności zmiennej objaśnianej stanowi zmienność wartości teoretycznych tej zmiennej, tj. informuje R² o tym, jaka część zmienności zmiennej objaśnianej Y zdeterminowana jest przez zmienną objaśniającą X.

• Dopasowanie modelu do danych jest tym lepsze, im współczynnik determinacji R² jest bliższy jedności.

Transformacja liniowa

Transformacja liniowa polega na sprowadzeniu za pomocą odpowiednich przekształceń, funkcji nieliniowych do funkcji liniowych względem występujących w niej parametrów.

Funkcja wykładnicza postaci

Transformacja liniowa polega na przekształceniu danych empirycznych, zawartych w wektorze y₁, y₂, ..., y_n i dotyczących zmiennej objaśnianej Y, za pomocą wzoru:

z_t = ln(y_t), t = 1, 2, …, n;

ponieważ

z_t = ln(y_t) = ln(b) + x_tln(a) = B + Ax_t, t = 1, 2, …, n.

Estymatory a*, b* parametrów a, b modelu wyjściowego obliczamy na podstawie MNK - estymatorów A*, B* parametrów A, B według wzorów:

a* = exp(A*); b* = exp(B*).

Funkcja potęgową postaci

Transformacja liniowa polega na przekształceniu danych empirycznych, zawartych w wektorze y₁, y₂, ..., y_n i dotyczących zmiennej objaśnianej Y, za pomocą wzoru:

z_t = ln(y_t), t = 1, 2, …, n;

oraz przekształceniu danych empirycznych, zawartych w wektorze x₁, x₂, ..., x_n i dotyczących zmiennej objaśniającej X, za pomocą wzoru:

u_t = ln(x_t), t = 1, 2, …, n,

ponieważ

ln(y_t) = ln(b) + aln(x_t) = B + au_t, t = 1, 2, …, n.

Estymator b* parametru b modelu wyjściowego obliczamy na podstawie MNK - estymatoru B* parametru B według wzoru:

b* = exp(B*).

Funkcja logarytmiczna postaci y_t = aln(x_t) + b

Transformacja liniowa polega na przekształceniu danych empirycznych, zawartych w wektorze x₁, x₂, ..., x_n i dotyczących zmiennej objaśniającej X, za pomocą wzoru:

u_t = ln(x_t), t = 1, 2, …, n,

ponieważ

y_t = aln(x_t) + b = b + au_t, t = 1, 2, …, n.

Estymatory a*, b* parametrów a, b modelu wyjściowego obliczamy za pomocą MNK na podstawie danych empirycznych {(u_t, y_t), t = 1, 2, …, n}.

Zadania

Funkcja wykładnicza

1. Dokonać właściwej transformacji liniowej dla modelu wykładniczego

2. Oszacować parametry A, B modelu liniowego za pomocą metody najmniejszych kwadratów.

3. Obliczyć wartości wektora z*_t = B* + A*x_t, t=1,2,...,n.

4. Obliczyć współczynnik determinacji
   .

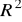
5. Obliczyć wartości estymatorów a*, b* parametrów a, b modelu wykładniczego

:
;

6. Obliczyć wartości linii regresji próby {y*_t, t=1,2,...,n} (wartości teoretyczne).

.

7. Dodać do wykresu wartości empirycznych (x_t, y_t), t=1,2,...,n linię regresji próby (x_t, y*_t), t=1,2,...,n.

8. Wzkorystując wykres wartości empirycznych (x_t, y_t), t = 1, 2, ..., n, oraz stosując funkcję „DODJ LINJĘ TRENDU” znaleźć wartości estymatorów a*, b* parametrów strukturalnych modelu oraz wartość R² współczynnika determinacji.

Funkcja potęgowa (...)

Funkcja logarytmiczna (...)

1

---