Laboratoryjne zajęcie N2

Specyfikacja zmiennych, występujących w modelu ekonometrycznym

Zmienne objaśniające w modelu ekonometrycznym z formalnego punktu widzenia powinny się odznaczać następującymi własnościami:

• mieć odpowiednio wysoką zmienność;

• być silnie skorelowane ze zmienną objaśnianą;

• być słabo skorelowane między sobą;

• być silnie skorelowane z innymi zmiennymi nie pełniącymi roli zmiennych objaśniających, które zmienne objaśniające reprezentują.

1. Eliminowania zmiennych quasi-stałych

Niech [x_1k, x_2k, … x_nk] będą realizacjami zmiennej X_k, k = 1, 2, …, K. Miarą poziomu zmienności zmiennej X_k jest współczynnik zmienności V_k, określony jako stosunek odchylenia standardowego S_k zmiennej X_k do jej średniej arytmetycznej m_k, czyli:

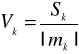
, (1)

gdzie

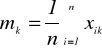
(2)

jest średnią arytmetyczną zmiennej X_k;

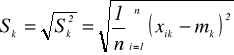
(3)

jest odchyleniem standardowym zmiennej X_k.

Eliminowanie zmiennych quasi-stałych na podstawie wartości współczynnika zmienności V_k odbywa się w sposób następujący.

1. Oblicza się współczynniki zmienności V_k dla poszczególnych badanych zmiennych X_k, k=1,2,…,K według wzorów (1), (2), (3).

2. Obiera się krytyczna wartość V_k^* współczynnika zmienności (np. V_k^* = 0,05).

3. Zmienna o numerze k, dla której jest spełniona nierówność

V_k ≤ V_k^* (4)

uznaje się za quasi-stałą i eliminuje się ze zbioru zmiennych kandydujących do roli objaśniających (k = 1, 2, …, K). Uważamy że zmienna te nie wnosi istotnych informacji o zmiennej objaśnianej.

Aby ocenić siłę liniowej zależności zmiennej objaśnianej Y i potencjalnych zmiennych objaśniających X₁, X₂, ..., X_K, oraz siłę liniowej zależności między potencjalnymi zmiennymi objaśniającymi X₁, X₂, ..., X_K, pomiędzy sobą, oblicza się współczynniki korelacji:

;
,

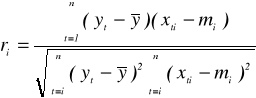
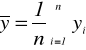
oraz

.

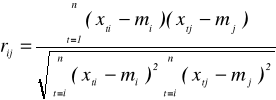
Współczynniki te są przedstawione w postaci wektora korelacji R₀, oraz macierzy R.

2. Prosta metoda grafowa

1. Wyznaczyć krytyczną wartość r* współczynnika korelacji według wzoru:

. (5)

2. Przeprowadzić eliminowanie związków nieistotnych: Współczynniki korelacji r_ks macierzy R, dla których zachodzi relacja |r_ks| ≤ r*, uznajemy za nieistotne i zastępujemy ich w macierzy R zerami. Zmodyfikowaną w ten sposób macierz R oznaczamy jako R', a ją elementy jako r'_ks.

3. Na podstawie macierzy R' budujemy graf, w którym wierzchołkami są potencjalne zmienne objaśniające X₁, X₂, … X_K , a wiązadłami występują współczynniki korelacji r'_ks ≠ 0.

4. Zmienne należące do różnych spójnych podgrafów traktujemy jako niezależne. Zostawiamy zmienne, reprezentowane przez punkty odosobnione.

5. Dla nie odosobnionych spójnych podgrafów określamy stopień g każdego węzła grafu, tj. liczbę wiązadeł, którymi jest on związany z innymi węzłami.

6. W każdym grafie spójnym wyróżniamy węzeł o maksymalnym stopniu g. Węzeł ten reprezentuje zmienną, która jest bezpośrednio związana z największą liczbą pozostałych zmiennych, będących węzłami tego samego spójnego podgrafu i w tym sensie gromadzi w sobie najwięcej informacji z pozostałych zmiennych.

7. Jeżeli w danym grafie spójnym jest kilka węzłów o takim samym maksymalnym stopniu g, to wybieramy spośród nich węzeł, charakteryzujący tą zmienną X_k, dla której współczynnik korelacji r_k ze zmiennej objaśnianej Y jest maksymalny.

Ostatecznie jako zmienne objaśniające pozostawiamy zmienne, reprezentujące punkty izolowane oraz wyróżnione z grafów spójnych według kryterium maksymalnej wartości g, oraz kryterium maksymalnej wartości r_k.