DEFINICJA LOGIKI­

łac. Logika, gr.logikos = zgodny z rozumowaniem.

Dyscyplina naukowa zaliczana do nauk filozoficznych, obejmująca logiczna teorię języka, czyli semiotykę logiczną, logikę formalną, czyli symboliczna, metodologię nauk i in.

• w węższym znaczeniu - logika dedukcji (rachunki logiczne), nauka o prawach wynikania.

• w szerszym znaczeniu - to zespół dyscyplin naukowych, dla których przedmiotem badań jest język i czynności badawcze (rozumowanie, definiowanie, klasyfikowanie, itp), których to analizę prowadzi się w celu podania takich reguł posługiwania się językiem i wykonywanie owych czynności, które czyniłyby tę działalność, możliwie najbardziej skuteczna.

W skład logiki jako nauki wchodzą:

SEMIOTYKA - (gr. dotycząca znaku) - ogólna teoria znaku obejmująca: semantykę, syntaktykę i pragmatykę, zajmująca się problemem typologii różnych postaci i odmian znaków, ich istotą i rolą, jaką pełnią w procesie porozumiewania się ludzi.

semantyka - (gr. oznaczający) - dział językoznawstwa zajmujący się badaniem znaczenia historii wyrazów, badanie wyrażeń językowych m.in. stosunku wyrażeń językowych do rzeczy przez nie oznaczanych oraz problemami precyzyjnego i ścisłego wypowiadania się.

syntaktyka - (gr. zestawiający, porządkujący) - dział gramatyki zajmujący się funkcja wyrazów w zdaniu oraz związkami i zależnościami między zdaniami; składnia).

pragmatyka - (gr. czynny) - nauka o ludzkim działaniu, zajmująca się stosunkiem (takim jak komunikowanie, wyrażane, rozumienie) między językiem a tymi, którzy się nim posługują.

LOGIKA FORMALNA - to dziedzina pouczająca nas o związkach zachodzących między zdaniami a przede wszystkim tym, jak ze zdań o pewnej określonej budowie wynikają inne zdania o pewnej określonej budowie, podaje reguły, określa schematy, formalną stronę wypowiedzi, analizuje wyrażenia.

OGÓLNA METODOLOGIA NAUK - - nauka o metodach badań naukowych, o skutecznych sposobach dociekania ich wartości poznawczej_

KATEGORIE SYNTAKTYCZNE - dwa wyrażenia należą do tej samej kategorii

syntaktycznej wtedy i tylko wtedy, gdy po zastąpieniu jednego wyrażenia przez drugie w danym wyrażeniu sensownym otrzymamy nadal wyrażenie sensowne.

np. zdanie: Jacek je jabłko. (zdanie ma sens),

Jacek je banana. (zdanie również jest sensowne, mimo zastąpienia wyrażenia 'jabłko" wyrazem "banan". Wyrazy: "jabłko" i "banan" należą do tej samej kategorii syntaktycznej

ale: w tym samym zdaniu, zastąpienie wyrazu "jabłko" wyrazem śpi - tworzy zdanie: Jacek je śpi, -które jest pozbawione sensu.

WYRAŻENIE SYNTAKTYCZNE - wyrażenie "w1"' wzięte w znaczeniu "z1" należy do tej samej kategorii syntaktycznej co wyrażenie "w2" wzięte w znaczeniu "z2" wtedy i tylko wtedy, gdy po zastąpieniu wyrażenia "w1" wziętego w znaczeniu "z1" przez wyrażenie "w2" wzięte w znaczeniu "z2" z wyrażenia sensownego otrzymuje się znowu wyrażenie sensowne.

Trzy podstawowe kategorie syntaktyczne:

1. nazwy,

2. Zdania,

3. Funktory

NAZWA - każdy przedmiot, o którym daną nazwę można zgodnie z prawda orzec, zachowując reguły przyjęte w języku, którego wyrażeniem jest ta nazwa.

Desygnat nazwy - łac. oznaczony) - przedmiot myśli odpowiadający wyrazowi.

ZDANIE -wyrażenie sensowne o charakterze oznajmującym; które można zakwalifikować jako prawdziwe lub fałszywe. Zdaniem logicznym jest wypowiedź, w której coś się o czymś orzeka. Znaczeniem zdania logicznego (jego treścią, sensem) jest sąd przez nie wyrażany. Zdaniem w sensie logicznym jest wyrażenie jednoznacznie stwierdzone na gruncie reguł danego języka, iż tak a tak jest lub tak a tak nie jest, czyli zdaniem w sensie logicznym jest takie wyrażenie, które albo jest prawdziwe albo fałszywe (tzw. dwuwartościowość).

Logika przyjmuje, że zdanie może być tylko oznajmujące (opisowe) i tylko takie zdanie są w logice rozważane.

Podstawowy podział zdań:

zdania proste - to takie wyrażenia, w których nie możemy wyróżnić mniejszej całości, która byłaby zdaniem (np. dziś jest ładna pogoda).

zdania złożone - to zdania, w których możemy wyróżnić mniejszą całość, które jest zdaniem (np. Pójdę do kina lub pójdę do teatru).

Trzy formy zdania:

1. twierdzenie, tj. wyrażenie o postaci "prawdą jest, że X", czyli takie, które można uznać za asercję (tj. sąd ogłoszony z przekonaniem o ich prawdziwości).

2. przeczenie, tj. wyrażenie o postaci "nieprawda, że x", czyli takie. które (zgodnie z regułami składni logicznej) można poprzedzić znakiem negacji,

3. supozycja, tj. Wyrażenie o postaci (np. okresu warunkowego "jeżeli x to y” , czyli takie, które w ścisłym sensie niczego nie stwierdza ani niczemu nie zaprzecza lecz wyraża jakieś przypuszczenie co do pewnego stanu rzeczy (tj. co do jego prawdziwości, fałszywości, możliwości, konieczności itp). Supozycja to rola znaczeniowa danego wyrażenia (nazwy) w wypowiedzi. Może być:

• prosta - oznacza określony swój desygnat,

• formalna - odnosi się do zbioru wszystkich swych desygnatów,

• materialna - nazywa wyrażenie równokształtne z samą ta nazwą.

Symbolicznie zdanie w logice określamy: 1 - prawdziwe, 0 - fałszywe

Prawda - cecha sądu przysługująca mu tylko wówczas, gdy w rzeczywistości jest właśnie tak, jak ów sąd głosi.

Fałsz - przeciwieństwo prawdy, jedna z dwu wartości logicznych, nieprawdziwość zdania (hipotezy, twierdzenia), jego niezgodność z rzeczywistością.

np. Dzisiaj pada deszcz. - prawda (1); Dzisiaj pada śnieg - fałsz (0)

RACHUNEK ZDAŃ - TEORIA ZDAŃ - to jeden z podstawowych działów logiki obejmujący wzory logiczne (logiczne schematy wnioskowania niezawodnego zmiennymi zdaniowymi występujące w postaci funkcji prawdziwościowych. Przedmiotem rachunku zdań jest badanie związków logicznych między zdaniami złożonymi, a zwłaszcza zachodzących między nimi strukturalnych stosunków bezpośredniego wynikania. operuje wyrażeniami:

• zmienne zdaniowe - oznaczane symbolicznie małymi literami: p, q, r, s, t. Za zmienne można podstawiać inne zdanie,

• funktory zdaniotwórcze od argumentów zdaniowych, czyli spójniki przyzdaniowe (negacja) i międzyzdaniowe (alternatywa, dysjunkcja, implikacja, koniunkcja, równoważność). objaśnienia funktora:

• negacja - "nie p", "nieprawda, że p"

• alternatywa (sumy logicznej) - "co najmniej jedno z dwojga: p lub q"

• alternatywa wyłączajaca - zwanej też dysjunkcja (niezgodność) - "p wyklucza się z q", "co najwyżej jedno z dwojga: albo p albo q"

• koniunkcja (iloczynu logicznego) - "p i q" (symbolicznie określana: •)

• implikacja - "jeżeli p to q" (symbolicznie określana: ⊃, →)

• równoważność - "p wtedy i tylko wtedy, gdy q"

wyrażenie złożone, stanowiące różnorodne kombinacje zmiennych i funktorów, zawierające niekiedy również kwantyfikatory.

Funkcja zdaniowa - wyrażeni zawierające zmienne nazwowe i znaki, z których co najmniej jedna jest wolna, a które -po podstawieniu stałych (nazw lub zdań) w miejsce tych zmiennych przekształca się w zdanie. Funkcja zdaniowa może być:

• ekstensjonalna - jeśli przekształcenie jej w zdanie prawdziwe (lub fałszywe) zależy jedynie od wartości logicznej zdań lub od denotacji (tj. zakresu nazwy) nazw podstawionych w niej za odpowiednie zmienne,

• intensjonalna - jeśli :przekształcenie jej w zdanie prawdziwe zależy jedynie od sensu wyrażeń podstawionych w miejsce zmiennych (a nie od ich prawdziwości lub fałszywości).

FUNKTORY -

każde wyrażenie nie będące zdaniem ani nazwą, służące najczęściej do konstruowania zdań lub nazw, lub innych wyrażeń bardziej złożonych.

Argument - to nazwy, zdania ,oraz inne wyrażenie związane z danym funktorem. np.

Jan - uczy - Piotra.

↓ ↓ ↓

nazwa funktor nazwa

np. Stanisław jest studentem i Michał jest studentem.

↓

funktor

Podział funktorów:

1. funktory nazwotwórcze - są to wyrażenia, które dodane do nazwy tworzą nazwę:

1. funktory nazwotwórcze od jednego argumentu nazwowego - to wyrażenie, które dodane do nazwy tworzy dalej nazwę.

np. Student (nazwa), pilny (funktor), Pilny (funktor nazwotwórczy) student.

2. funktory nazwotwórcze od dwóch argumentów nazwowych - to wyrażenie, które łączy dwie nazwy i w wyniku tego połączenia powstaje dalej nazwa.

np. słowo "i" w zdaniu: Malarz i poeta

2. funktory zdaniotwórcze - to funktory, które łączą dwa zdania tworząc nowe zdanie.

1. funktory zdaniotwórcze od jednego argumentu nazwowego - to wyrażenie, które dodane do zdania tworzy nowe zdanie. np. słowo "je"

2. funktory zdaniotwórcze od dwóch argumentów nazwowych - to wyrażenie, które łączy dwa zdania, w wyniku tego połączenia powstaje nowe zdanie.

1. Pójdę do kina.

2. Pójdę do teatru.

3. Pójdę do kina lub pójdę do teatru.

(funktor)

Funktory prawdziwościowe, to takie funktory, które pozwalają nam określić zdanie, jeżeli znamy wartość argumentów tego funktora.

Funktor negacji ­

NEGACJA - (rac. zaprzeczenie, odrzucenie) - w języku potocznym jest odpowiednikiem przeczenia. ma postać słowną: "nieprawdą jest, że", "nie jest tak, że".

symbol: "~"

Przy pomocy tego funktora tworzona jest funkcja zdaniowa negacji: -p

Tabelka prawdziwościowa mówi nam, jaką wartość będzie miało zdanie utworzone przy pomocy tego funktora:

p	~ p
1	0
0	1

Funktor negacji zmienia wartość zdania.

Funktor koniunkcji ­

KONIUNKCJA (łac. połączenie)- zwana iloczynem logicznym - to zdanie złożone z dwu lub więcej zdań, prawdziwe wtedy i tylko wtedy, gdy każde ze zdań składowych jest prawdziwe (odpowiednikiem koniunkcji w języku jest zdanie złożone ze spójnikiem "i')

Najczęściej oznaczany za pomocą spójnika: "i, oraz, a, chociaż, ale, lecz"

symbol: „•”, „ ∧”

Przy pomocy tego funktora zdanie ma postać: p • q

Tabelka:

p	q	P•q
1	1	1
1	0	0
0	1	0
0	0	0

Funktor alternatywy

ALTERNATYWA - (łac. zmieniam kolejno) zdanie złożone współrzędnie, które jest prawdziwe, gdy przynajmniej jedno ze zdań składowych jest prawdziwe.

oznaczana spójnikiem: "lub" symbol: v

Przy pomocy tego funktora zdanie ma postać: p v q

Tabelka:

p	q	p v q
1	1	1
1	0	1
0	1	1
0	0	0

Alternatywa rozłączna:

oznaczana słownie: "albo p, albo q"

symbol: ⊥

Przy pomocy tego funktora zdanie ma postać: p ⊥ q

Tabelka:

p	q	p⊥q
1	1	0
1	0	1
0	1	1
0	0	0

Alternatywa - dysjunkcja oznaczana słownie: "bądź p, bądź q"

symbol: „ / ”

Przy pomocy tego funktora zdanie ma postać: p / q

Tabelka:

p	q	p / q
1	1	0
1	0	1
0	1	1
0	0	1

Funktor implikacji ­

IMPLIKACJA -(łac. związanie, pouczenie) zdanie złożone, mające swój odpowiednik w okresach warunkowych rzeczywistych języka naturalnego, które jest prawdziwe wówczas, gdy nie jest tak, iż jego poprzednik (człon pierwszy, następujący po słowie „jeżeli”) jest prawdziwy, a następnik (człon drugi, następujący po słowie "to”) jest fałszywy.

oznaczana słownie: "jeżeli p, to q"

symbol: ⊃ , →

Przy pomocy tego funktora zdanie ma postać: p ⊃ q

poprzednik implikacji następnik implikacji

Tabelka:

p	q	p ⊃q
1	1	1
1	0	0
0	1	1
0	0	1

Nie można zamieniać miejscami poprzednika z następnikiem. Implikacja jest zdaniem fałszywym jeżeli poprzednik jest prawdziwy a następnik fałszywy. Z prawdy nie może wynikać fałsz!

RÓWNOWAŻNIK

równoważność - stosunek zachodzący między wyrażeniami mającymi tą samą wartość logiczną (tzw. równoważność implikacyjna), polegający na tym, że wyrażenia te wzajemnie z siebie wynikają logicznie.

najczęściej oznaczany za pomocą spójnika: "zawsze i tylko wtedy, jeżeli p to q"

symbol: Ξ

Przy pomocy tego funktora zdanie ma postać: p Ξ q

Tabelka:

p	q	p Ξ q
1	1	1
1	0	0
0	1	0
0	0	1

Ćwiczenia - obliczenia wartości zdaniowej:

[(p •q) v p] ⊃ (p⊥q)

p	q	P•q	(p•q) v p	p	q	p⊥q	[ ] ⊃ ( )
1	1	1	1	1	1	0	0
1	0	0	1	1	0	1	1
0	1	0	0	0	1	1	1
0	0	0	0	0	0	0	1

[(~ p / q) ⊥ p)] • ( p ⊃ q)

p	q	~ p	~ p / q	⊥ p	~ p	~ p ⊃ q	[ ] • ( )
1	1	0	0	0	0	1	0
1	0	0	1	0	0	1	0
0	1	1	0	0	1	1	0
0	0	1	1	1	1	0	0

Istnieją takie funkcje zdaniowe, które dla wszystkich możliwych podstawień zawsze są zdaniem prawdziwym. Jest to tzw. prawo logiczne lub tautologia.

TAUTOLOGIA - to schemat zdania, w którym każde zdanie podpadające pod ten schemat jest prawdziwe (np. każde A jest A).

Jeżeli pada deszcz, to ulice są mokre i wiadomo, że ulice są mokre a zatem pada deszcz

„p„ „q„ • „q” ⊃ „p”

[ (p ⊃ q) • q] ⊃ p

Zwroty: a zatem, wobec tego" mówią, która część zdania jest następnikiem, a która poprzednikiem.

Jeżeli pada deszcz to ulice są mokre i nieprawdą jest, że ulice są mokre, zatem nieprawdą

p q • ~ q ⊃

jest, że pada deszcz

~ p

[ ( p ⊃q) • ~ q] ⊃ ~ p

p	q	~ p	(p ⊃q )	(p ⊃q) • ~ q	~ p	[( p ⊃q) • ~ q]⊃ ~ p
0	0	1	1	1	1	1
0	1	0	1	0	1	1
1	0	1	0	0	0	1
1	1	0	1	0	0	1

Jeżeli Piotr zasztyletował kogoś to byt na miejscu zbrodni. Okazuje się, że nie było go na

P ⊃ q ~ q

miejscu zbrodni. Wnioskujemy wiec, że to nie on zasztyletował kogoś.

• ~ p

[ ( p⊃ q ) • ~ q ] ⊃ ~p

Jeżeli Jan dokładnie przeczytał podręcznik (p), to ~ (⊃)jeżeli ponadto chodził na wykłady (q), to (⊃) ma szansę zdać egzamin (r). Zatem (⊃) jeżeli nieprawda, że Jan dokładnie przeczytał podręcznik (~p) lub (v) nieprawda, że chodził na wykłady ( ~q), to nieprawda, że ma szansę zdać egzamin (~r)

[p ⊃(q ⊃r)] ⊃[~p v ~q) ⊃ ~r]

	Konstrukcje zdaniowa	Zapis symboliczny
1	Jeżeli p, to q, to r	[ p ⊃( q ⊃r)]
2	Jeżeli p, to q lub r	[p ⊃ (q v r)]
3	Jeżeli p, to q. Lub r	[(p ⊃q) v r]
4	Jeżeli p lub q, to r	[(p v q) ⊃ r]
5	Jeżeli p, to q i r	p ⊃ (q • r )
6	Jeżeli p i q , to r	(p • q) ⊃ r
7	zawsze i tylko wtedy jeżeli p, to jeżeli q, to r	p ≡ (q ⊃r)
8	zawsze i tylko wtedy jeżeli p to, q lub r	p ≡ (q v r)
9	zawsze i tylko wtedy jeżeli p to, q. lub r	(p ≡ q) v r
10	zawsze i tylko wtedy jeżeli p lub q, to r	(p v q) ≡ r
11	zawsze i tylko wtedy jeżeli p, to q i r	p ≡(q • r )
12	zawsze i tylko wtedy jeżeli p i q, to r	(p • q) ≡r

TWIERDZENIE - teza teorii wyprowadzana za pomocą określonych przekształceń przyjętych w danej teorii aksjomatów.

Uzasadnianie twierdzeń - twierdzenie można uznać za prawdziwe tylko wtedy, gdy zostanie udowodnione.

Postulat racji dostatecznych - za prawdziwe należy uznać tylko takie zdanie, które może być należycie uzasadnione. Każda dyscyplina naukowa ma swoje zasady (sposoby) uzasadniania prawdziwości tezy (założenia).

Aksjomat - tradycyjnie - twierdzenie bezspornie prawdziwe, pewnik. Także naczelne twierdzenie systemu dedukcyjnego, przyjmowane w nim bez dowodu jako główna i ostateczna przesłanka dowodzenia wszelkich innych twierdzeń tego systemu.

SPOSOBY UDOWADNIANIA PRAWDZIWOŚCI TWIERDZEŃ:

BEZPOŚREDNIE POŚREDNIE

POSTRZEŻENIA POSTRZEŻENIA

ZEWNĘTRZNE WEWNĘTRZNE

Udowodnić prawdziwość twierdzenia możemy:

a) bezpośrednio - gdy udowadniamy prawdziwość twierdzenia w drodze doświadczenia (za pomocą zmysłów) tj:

- postrzeżenie --oznacza proces poznawczy polegający na odzwierciedleniu przedmiotów, zjawisk świata zewnętrznego oraz procesów zachodzących wewnątrz organizmu.

-postrzeżenia zewnętrzne (zmysłowe) dotyczą~; świata zewnętrznego (poza człowiekiem), -postrzeżenia wewnętrzne ( introspekcja) dotyczą procesów zachodzących wewnątrz organizmu człowieka np. uczucie głodu, uświadomienie bólu, utraty pamięci).

Bodźce ze świata zewnętrznego są odbierane przez zmysły i w wyniku posiadanej wiedzy analizowane przez umysł.

Ale bodźce mogą być zdeformowane np. przez obserwację przez mgłę, szum, deformację zmysłów (np. zmęczenie, choroba oczu, niedosłuch), nieprawidłowy odbiór bodźców może być skorygowany przez porównanie z innymi ludźmi.

Obserwacja - to rozmyślne postrzeganie, celowe, zamierzone;

obserwacja niezamierzona - widzimy wiele elementów, ale ich postrzeganie nie jest przez nas zamierzone, jest mimowolne.

Eksperyment - zabieg przedsiębrany w celu dokonania obserwacji, który bądź wywołuje samo obserwowane zjawisko, bądź wpływa na jego przebieg. Celem eksperymentu jest stworzenie określonych warunków do zaobserwowania ich wpływu na poszczególne parametry.

b) pośrednio - gdy w dowodzeniu powołujemy się na udowodnione wcześniej twierdzenia. wynikają z innych zdań wcześniej przyjętych za prawdziwe w tym przypadku mamy do czynienia z wnioskowaniem.

WNIOSKOWANIE CZYLI - INFERENCJA ­

- w węższym rozumieniu - jest to dobieranie następstw dla zdań pewnych, już uznanych za prawdziwe,

- w szerszym rozumieniu - jest to proces myślowy, w którym na podstawie zdań już uznanych (za prawdziwe) dochodzi się bądź do nowego zdania dotąd nie uznawanego, bądź do wzmocnienia innego zdania w jakimś stopniu już uznanego. Wszelkie wnioskowania dzielą się na niezawodne i zawodne, czyli uprawdopodobniające. Do niezawodnych należą wnioskowanie dedukcyjne, a jego szczególną odmianą jest wnioskowanie sylogistyczne z dwóch przesłanek Wśród różnych rodzajów wnioskowań zawodnych wyróżnia się wnioskowanie dedukcyjne, indukcyjne, analogia.

Reguły wnioskowania - dyrektywy lub reguły dowodzenia - reguły logicznie poprawnego przekształcania zdań, pozwalające uznawać pewne zdania na podstawie innych uznanych już zdań:

• reguła odrywania - zgodnie z którą, jeżeli uznany jest okres warunkowy (implikacja, notacja logiczna) oraz jego poprzednik, wolno zawsze uznać następnik;

• reguła podstawiania - która pozwala na uznanie każdej formy powstałej przez podstawienie wyrażeń sensownych za zmienne występujące w danej, uprzednio już uznanej formule,

• reguła zastępowania (albo definicji) według której każde wyrażenie wolno zastąpić wyrażeniem równoważnym.

Przesłanka - to zdanie, na podstawie którego uznaje się inne zdanie za prawdziwe.

Wniosek - to zdanie, które uznaje się za prawdziwe w wyniku wnioskowania.

Entymemat - (gr. myśl, zamysł)) wnioskowanie dedukcyjne, w którym przemilczało się jakąś przesłankę, najczęściej ze względu na ich oczywistość).

Przesłanka entymematyczna - przesłanka pominięta we wnioskowaniu.

Wnioskowanie może przebiegać wg schematów.

Ogólne schematy, wg których przebiega wnioskowanie, nazywamy schematami inferencyjnymi.

Inferencja - (tac. wnioskuję) - proces myślowy, w którym na podstawie zdań już uznanych za prawdziwe dochodzi się bądź do uznania nowego zdania dotąd nie uznanego, bądź wszelkie wnioskowania dzielą się na niezawodne i zawodne, czyli uprawdopodobniają. Do niezawodnych należą wnioskowanie dedukcyjne; a jego szczególną odmianą jest wnioskowanie "sylogistyczne' z dwóch przesłanek Wśród różnych rodzajów wnioskowań zawodnych wyróżnia się wnioskowanie: redukcyjna, indukcyjne, analogia.

Rodzaje wnioskowań:

Wnioskowania:

Wnioskowania niezawodne Wnioskowania zawodne:

wnioskowania wnioskowania wnioskowania

redukcejne z analogi indukcyjne:

indukcja niezupełna

indukcja zupełna

• wnioskowania niezawodne - to schematy, które zawsze prowadzą od prawdziwych przesłanek do prawdziwych wniosków.

• wnioskowanie zawodne (uprawdopodobniające) - to schematy wnioskowania, które nie zawsze prowadzą od prawdziwych przesłanek do prawdziwych wniosków.

Rodzaje wnioskowań zawodnych:

• wnioskowanie redukcyjne - (łac. odprowadzenie z powrotem) - to takie wnioskowanie, w którym z wniosku wynika przesłanka, (chociaż z przesłanek nie wynika wniosek); dobieranie do danego zdania uznanego za prawdziwe takiego zdania, z którego to pierwsze logicznie wynika.

• wnioskowanie z analogii -(gr. odpowiedni, stosowny) - wnioskowanie o posiadaniu pewnej cechy przez dany przedmiot na podstawie jego podobieństwa do innych przedmiotów posiadających tę cechę . Jest to wnioskowanie mające niewielką wartość dowodową, stosowane jako metoda prowadząca do przypuszczeń,

• wnioskowanie indukcyjne - (łac. wprowadzenie) - rozumowanie polegające na wyprowadzeniu wniosków ogólnych z przesłanek będących ich poszczególnymi przypadkami. Szerzej - metoda polegająca na dokonywaniu obserwacji i eksperymentów, wyprowadzaniu na tej podstawie uogólnień oraz formułowaniu hipotez i ich weryfikacji; na podstawie wielu jednostkowych przesłanek stwierdzających, ze poszczególne badane przedmioty danego rodzaju mają pewną cechę, wnioskuje się, że każdy przedmiot tego rodzaju posiada tę cechę.

Rodzaje wnioskowań indukcyjnych:

• indukcja zupełna - ilość przedmiotów jest ograniczona i można sprawdzić każdy przedmiot. Jest to wnioskowanie niezawodne.

• indukcja niezupełna ­

Rodzaje klasycznych zdań kategorycznych dotyczą wnioskowań niezawodnych,

jest ich 4:

Ogólno - twierdzące	S a P	każde S jest P (np. każdy ssak jest zwierzęciem lądowym)
Ogólno - przeczące	S e P	żadne S nie jest P (np. żaden ssak nie jest rybą)
Szczegółowo - twierdzące	S i P	niektóre S nie jest P (np. niektóre ssaki są drapieżne)
Szczegółowo - przeczące	S o P	niektóre S nie jest P (np. niektóre ssaki nie są zwierzętami)

ROZŁOŻENIE TERMINU KLASYCZNYCH ZDAŃ KATEGORYCZNYCH

Pod technicznym określeniem pojęcia „rozłożenie terminu” rozumie się wzięcie terminu w całym zakresie. Termin jest wzięty w całym zakresie wtedy, gdy mowa jest o wszystkich jego desygnatach.

1. Zdania ogólno - twierdzące

S a P rozłożony jest tylko podmiot

2. Zdania ogólno - przeczące

S e P rozłożony jest podmiot i orzecznik

3. Zdania szczegółowo - twierdzące

S i P nie jest rozłożony ani podmiot ani orzecznik

4. Zdania szczegółowo - przeczące

S o P rozłożony jest orzecznik

SPOSOBY WNIOSKOWAŃ

Wyróżniamy dwa rodzaje wnioskowań:

Wnioskowanie bezpośrednie - polega na tym, że do wniosku dochodzi się na podstawie jednej przesłanki.

Wnioskowanie pośrednie - polega na tym, że do wniosku dochodzi się na podstawie przynajmniej dwóch przesłanek.

Do wnioskowań bezpośrednich logika formalna zalicza:

• Konwersje

• Obwersje

• Kontrapozycje

• Opozycję zdań czyli wnioskowanie z kwadratu logicznego.

KONWERSJE

Jest to odmiana wnioskowania bezpośredniego, polegająca na wyprowadzeniu z klasycznego zdania kategorycznego jego odwrócenia. Wniosek wyprowadza się odwracając przesłankę.

Wyróżnia się dwa rodzaje konwersji:

1. Konwersja prosta - polega na zamianie miejscami podmiotu i orzecznika w zdaniu odwracanym.

Konwersji prostej podlegają dwa rodzaje zdań:

Zdania ogólno przeczące typu S e P (żadne S nie jest P)

S e P ⇒^k P e S

oraz zdania szczegółowo twierdzące typu S i P

S i P ⇒^k P i S (niektóre P są S)

2. Konwersja ograniczona - polega na zamianie miejscami podmiotu i orzecznika oraz zmianie ilości zdania. Podlegają jej zdania ogólno twierdzące typu S a P (każde S jest P) a zdania szczegółowo przeczące konwersji nie podlegają !!!

S a P = P i S

• ↑

(zdanie ogólne) (zdanie szczegółowe)

Przykłady:

Każdy człowiek jest ssakiem. (zdanie podlega konwersji ograniczonej)

S a P = P i S

Niektóre ssaki są ludźmi.

Niektórzy mężczyźni nie są studentami. ( to zdanie nie podlega konwersji)

Niektórzy mężczyźni są studentami. (to zdanie szczegółowo - twierdzące)

S e P ⇒ P e S

Niektórzy studenci są mężczyznami.

Żadna kobieta nie jest mężczyzną. (to zdanie ogólno - przeczące) dokonujemy konwersję prostą S e P = P e S

OBWERSJA

Jest odmianą wnioskowania bezpośredniego i polega na wyprowadzeniu ze zdania twierdzącego równoważnego mu zdania przeczącego lub odwrotnie, ze zdania przeczącego równoważnego mu zdania twierdzącego. Obwersji podlegają wszystkie rodzaje klasycznych zdań kategorycznych. Aby dokonać obwersji należy: zmienić jakość zdania a następnie zanegować orzecznik.

S a P ⇒⁰ S e (~ P)

S e P ⇒⁰ S a (~P)

S i P ⇒ S o (~P)

S o P ⇒⁰ S i (~P)

Każdy człowiek jest ssakiem. (zdanie ogólno - twierdzące)

S a P ⇒⁰ S e (~P) po przekształceniu- Żaden człowiek nie jest ssakiem.

Żadna kobieta nie jest mężczyzną. (zdanie ogólno- przeczące)

S e P ⇒⁰ S a (~P)

Każda kobieta jest nie mężczyzną .

Niektóre ssaki nie są nie ludźmi.

Niektórzy mężczyźni nie są studentami. (zdanie szczegółowo przeczące)

S o P ⇒⁰ S i (~P)

Niektórzy mężczyźni są nie studentami.

KONTRAPOZYCJA

To rodzaj wnioskowania bezpośredniego, powstaje przez kombinacje obwersji i konwersji.

Wyróżniamy dwa rodzaje kontrapozycji:

-częściowa

-zupełna.

Kontrapozycji częściowej dokonuje się przekształcając klasyczne zdanie kategoryczne w następujący sposób: najpierw dokonujemy obwersji i tak otrzymane zdanie podlega konwersji.

A⇒⁰ A` ⇒^k A``

S a P ⇒⁰ S e (~P) ⇒^k (~P) e S

S e P⇒⁰ S a (~P) ⇒^k (~P) i S

S i P ⇒⁰ S o (~P) ⇒^k nie podlega konwersji

S o P ⇒⁰ S i (~P) ⇒^k (~P) i S

Kontrapozycji zupełnej dokonuje się w następujący sposób: najpierw dokonujemy obwersję, konwersję i obwersję.

A ⇒⁰ A` ⇒^k A`` ⇒⁰ A```

S a P ⇒⁰ S e (~P)⇒^k (~P) e S ⇒⁰(~P a (~S)

S e P ⇒⁰S a (~P) ⇒^k (~P) i S ⇒⁰ (~P) o (~S)

S i P nie podlega kontrapozycji zupełnej

S o P ⇒⁰ S i (~P) ⇒^k (~P) i S ⇒⁰ (~P) o (~S)

Przykłady:

Kontrapozycja częściowa lub zupełna.

Żadna kobieta nie jest mężczyzną. (to zdanie ogólno - przeczące)

S e P ⇒⁰ (S a (~P) ⇒^k (~P) i S ⇒⁰ (~P) o (~S)

↓

Każda kobieta jest nie mężczyzną.

Niektórzy nie mężczyźni są kobietami.

Niektórzy nie mężczyźni nie są nie kobietami.

Przykład:

Niektórzy mężczyźni nie są studentami. (kontrapozycja częściowa)

S o P ⇒⁰ S i (~P) ⇒^k (~P) i S

Niektórzy mężczyźni są nie studentami.

Niektórzy nie studenci są mężczyznami.

Przykład:

Tylko ssaki są ludźmi.

Tylko S są P ⇒ P a S (każde P są S)

Tylko S nie są P ⇒ każde (~S) jest P czyli (~ S a P)

Każdy człowiek jest ssakiem. (zrobić kontrapozycję zupełną!)

S a P ⇒⁰ S e (~ P) ⇒^k (~P) e S ⇒⁰ (~P) a (~S)

Żaden człowiek nie jest nie ssakiem.

Żaden nie ssak nie jest człowiekiem. (~P e S)

Każdy nie ssak jest nie człowiekiem (~P) a (~S)

Niektóre swetry są wełniane.. (kontrapozycja zupełna)

Nie podlega konwersji zupełnej!!!

OPOZYCJA ZDAŃ CZYLI KWADRAT LOGICZNY

Jest to obrazowe przedstawienie zależności zachodzących po między klasycznymi zdaniami kategorycznymi o tym samym podmiocie i tym samym orzeczniku.

/ dysjunkcja

S a P przeciwieństwo S e P

⊃

S i P podprzeciwieństwa S o P

V alternatywa zwykła

Relacja przeciwieństwa zachodzi pomiędzy zdaniem ogólno- twierdzącym typu S a P

a zdaniem ogólno -przeczącym S e P. Charakteryzuje się ona tym, że obydwa zdania mogą być jednocześnie fałszywe natomiast nie mogą być jednocześnie prawdziwe.

Relacja podprzeciwieństwa zachodzi pomiędzy zdaniami szczegółowo twierdzącymi S i P

a zdaniami szczegółowo przeczącymi S o P. Charakteryzuje się tym, że mogą być obydwa zdania prawdziwe a nie mogą być jednocześnie fałszywe.

Relacja sprzeczności zachodzi między zdaniem szczegółowo przeczącym S a P

a zdaniem szczegółowo przeczącym S o P lub między zdaniem ogólno -przeczącym S e P a zdaniem szczegółowo twierdzącym S i P. Charakteryzuje się ona tym, że obydwa zdania nie mogą być jednocześnie ani fałszywe ani prawdziwe.

Relacja nadrzędności zachodzi pomiędzy zdaniem ogólno- twierdzącym typu S a P a zdaniem szczegółowo twierdzącym S i P oraz pomiędzy zdaniem ogólno- przeczącym S e P i szczegółowo przeczącym typu S o P. Relacja charakteryzuje się tym, że jeżeli zdanie ogólne jest zdaniem prawdziwym to zdanie podrzędne musi być zdaniem prawdziwym.

Jeżeli zdanie ogólne jest fałszywe to zdanie szczególne jest nieokreślone, może być zarówno prawdziwe jak i fałszywe.

Relację przeciwieństwa możemy zapisać przy pomocy funktora dysjunkcji.

Przykład:

Przeprowadzić wnioskowanie z kwadratu logicznego jeżeli wiadomo, że prawdziwe jest zdanie „każdy adwokat jest prawnikiem”.

S a P (zdanie ogólno twierdzące)

S a P / S e P

⊃

S i P S o P

v

S a P / S e P

^{1 1 0}

S a P ⊥ S o P

^{1 1 0}

S a P ⊃ S i P

^{1 1 1} To zdanie jest prawdziwe.

Przykład:

Fałszywe jest zdanie sprzeczne do zdania: „Każdy adwokat jest prawnikiem” (jest to zdanie ogólno -twierdzące)

S o P (to zdanie sprzeczne, czyli fałszywe)

⁰

S o P v S i P

^{0 1 1}

S o P ⊥ S a P

^{0 1 1}

S e P ⊃ S o P

^{0 1 0}

Przykład:

Przeprowadź wniosek z kwadratu logicznego jeżeli wiadome jest, że prawdziwe jest zdanie podrzędne do zdania: ”Tylko prawnicy są adwokatami.” - po przekształceniu do klasycznego zdania kategorycznego

Każdy adwokat jest prawnikiem. S a P

Niektórzy adwokaci są prawnikami. S i P

S a P ⊃ S i P

^{1/0 1 1}

S i P ⊥ S e P

^{1 1 0}

S i P v S o P

^{1 1 1/0} Zdania te są nieokreślone, mogą być prawdziwe i fałszywe.

Przykład:

Przeprowadź wniosek z kwadratu logicznego. Fałszywe jest zdanie przeciwne do zdania „Żaden kawaler nie jest bigamistą”.

S e P (zdanie ogólno- przeczące)

S a P jest zdaniem fałszywym

S a P / S e P

^{1 1 1/0}

S a P ⊥ S o P

^{0 1 1}

S a P ⊃ S i P

^{0 1 1/0}

Przykład:

Przeprowadź wnioskowanie z kwadratu logicznego jeżeli wiadomo, że fałszywe jest zdanie przeciwne do zdania: „Tylko nie prokuratorzy nie są prawnikami.” (zdanie trzeba przekształcić na klasyczne zdanie kategoryczne)

Każdy prokurator jest prawnikiem.

Tylko S nie są P.

S e P jest 0 (fałszywe)

S e P / S a P

^{0 1 1/0}

S e P ⊥ S i P

^{0 1 1}

S e P ⊃ S o P

^{0 1 1/0}

Przykład:

Przeprowadź wnioskowanie z kwadratu logicznego. Fałszywe jest zdanie nadrzędne do zdania: „Niektórzy uczniowie nie są studentami”.

S o P (zdanie szczegółowo - przeczące) S E P 0 (fałszywe)

S e P / S a P

^{0 1 1/0}

S e P ⊥ S a P

^{0 1 1/0}

S e P ⊃ S o P

^{0 1 1}

Przykład:

Przeprowadź wnioskowanie. Prawdziwe jest zdanie sprzeczne do zdania; „Tylko recydywiści są włamywaczami”.

Każde P są S

Każdy włamywacz jest recydywistą,

P a S

Niektórzy włamywacze nie są recydywistami.

S o P

S o P v S i P

^{1 1 0/1}

S a P ⊥ S o P

^{0 1 1}

S e P ⊃ S o P

^{0/1 1 1}

WNIOSKOWANIA POŚREDNIE to: klasyczny sylogizm kategoryczny należy do wnioskowań pośrednich, bo wnioskujemy z dwóch przesłanek.

Klasycznym sylogizmem kategorycznym nazywamy wyrażenie zdaniowe mające postać implikacji w której poprzednikiem jest koniunkcja dwóch klasycznych zdań kategorycznych, natomiast następnik tej implikacji stanowi konkluzję czyli wniosek.

[M a P • S o M ] ⊃ S e P (ma postać implikacji)

M a P

S o M

S e P (to równorzędny zapis)

Występują trzy klasyczne zdania kategoryczne i występują trzy terminy:

S - termin mniejszy jest to ta nazwa, która we wniosku występuje jako podmiot.

P - termin większy jest to ta nazwa, która jest orzecznikiem we wniosku

M - termin średni jest to nazwa, która występuje w obydwu płaszczyznach a nie występuje we wniosku.

Przesłanka mniejsza jest to ta przesłanka w której występuje termin mniejszy i termin średni.

Przesłanka większa to ta w której występuje termin większy i termin średni.

Pierwszą przesłankę pisze się większą a później mniejszą.

FIGURY SYLOGICZNE są to schematy wnioskowań sylogicznych wyróżnione ze wzg. na położenie terminu średniego.

Jeżeli w przesłance termin średni jest podmiotem:

M P

S M I Figura

S P

P M

S M II Figura

S P

M P

M S III Figura

S P

P M

M S IV Figura

S P

Przykłady:

Niektórzy ludzie są wysocy. - pierwsza przesłanka

M i P M i P

Niektórzy ludzie są blondynami.

M i S M i S

Niektórzy blondyni są wysocy. S i P

S i P

Żaden adwokat nie jest sędzią.

Niektórzy sędziowie nie są kobietami.

Niektóre kobiety są adwokatami.

• ↓

Podmiot S P

P e M

M o S

S i P

Każdy prawnik jest człowiekiem.

M a P

Niektórzy prawnicy są sędziami.

M i S

Każdy sędzia jest człowiekiem.

S a P (termin większy - orzecznik)

M - termin średni

M a P

M i S

S a P

WARUNKI POPRAWNOŚCI SYLOGIZMU

Sylogizm jest poprawny gdy spełnia następujące warunki:

1. Występują w nim tylko trzy terminy (nazwy).

2. Termin średni przynajmniej w jednej z przesłanek musi być rozłożony.

3. Termin rozłożony we wniosku musi być rozłożony w przesłance.

4. Następnie obie przesłanki nie mogą być zdaniami przeczącymi.

5. Obie przesłanki nie mogą być zdaniami szczegółowymi.

6. Jeżeli jedna z przesłanek jest zdaniem przeczącym, to wniosek nie może być zdaniem twierdzącym.

7. Gdy jedna z przesłanek jest zdaniem szczegółowym, to wniosek nie może być zdaniem ogólnym.

8. Wniosek nie może być zdaniem przeczącym jeżeli żadna z przesłanek nie jest zdaniem przeczącym.

Sylogizm jest poprawny gdy spełnia wszystkie te osiem przesłanki.

M a P

S a M

S a P Ten sylogizm jest poprawny.

S a M

M o P

S o P Ten sylogizm jest niepoprawny bo termin średni nie jest rozłożony.

S a M (termin średni)

S i P wniosek

M o P (zdanie szczegółowo przeczące)

M a S (zdanie ogólno - twierdzące)

S o P

Dobrać drugą przesłankę!

M e P (to zdanie ogólno - przeczące - przesłanka większa)

...........

S a P (zdanie ogólno - twierdzące)

S a M M a S

S e M M e S

S i M M i S

S o M M o S Ten sylogizm jest niepoprawny.

P a M (zdanie ogólno - twierdzące)

S e M lub M e S

S e P (zdanie ogólno - przeczące)

S a M M a S

S e M M e S

S i M M i S

S o M M o S

Przykład:

Dobrać drugą przesłankę!

S i M (przesłanka mniejsza - zdanie szczegółowo - twierdzące)

...........

S o P (zdanie szczegółowo - przeczące)

M a P P a M S podmiot - termin mniejszy

M e P P e M P orzecznik - termin większy

M i P P i M M termin średni

M o P P o M

Możliwe jest M e P lub P e M.

Przykład:

Dobieramy wniosek aby sylogizm był poprawny.

M a P (zdanie ogólne)

M i S (zdanie szczegółowo - twierdzące)

S i P

S a P

S e P

S i P

S o P

Jedynym wariantem jest S i P.

P i M (zdanie szczegółowo - twierdzące)

M a S (zdanie ogólne)

S I P

S a P

S e P

S i P

S o P

Jedynym wariantem jest S i P.

M i P (zdanie szczegółowo - twierdzące - nie jest rozłożony ani podmiot ani orzecznik)

S e M (zdanie ogólno - przeczące - rozłożony jest podmiot i orzecznik)

S * P

S a P

S e P

S i P W tym przykładzie nie uda się przesłanki dobrać!

S o P

N A Z W Y

Nazwą jest taki wyraz lub wyrażenie, które w zdaniu o rzeczach lub osobach nadaje się na podmiot lub orzecznik.

A jest B

lub

Nazwą nazywamy taki wyraz lub wyrażenie, które w zdaniu o postaci A jest B można wstawić za zmienną A (czyli podmiot) lub B (czyli orzecznik).

Np.

Słońce jest planetą.

A B

Jacek jest wysokim mężczyzną.

A B

Podmiot występuje przed słowem „jest”, a orzecznik występuje po słowie „jest”.

Przykład:

Mój ukochany pies jest nowofundlandem.

Podmiot orzecznik

On jest uczniem.

A B

W logice nazwa nie oznacza rzeczownika. Nazwą może być: rzeczownik, zaimek, przymiotnik.

DESYGNAT NAZWY - nazywamy przedmiot oznaczony przez daną nazwę. Lub

Desygnat jest to przedmiot o którym zgodnie z prawdą daną nazwę możemy orzekać. Książka którą mamy przed oczami jest desygnatem nazwy „książka”; ten, kto tę książkę napisał, jest desygnatem nazwy „człowiek”; to, co mamy pod nogami, jest jedynym desygnatem nazwy „glob ziemski”, itp. Jeżeli weźmiemy do ręki książkę i powiemy: „To jest książka” - to powiemy prawdę; jeżeli powiemy :”To jest chmura”- to powiemy nieprawdę.

Nazwa oznacza swe desygnaty.

ZAKRES NAZWY - jest to zbiór wszystkich desygnatów danej nazwy. A wiec zakres nazwy „student”, to zbiór wszystkich z osobna wziętych osób, z których każda jest studentem - natomiast nie chodzi tu o całość taką, jak ogólnoświatowa organizacja studencka.

TREŚĆ NAZWY - jest to zespół cech charakterystycznych, które musi posiadać przedmiot, aby był uznany za desygnat danej nazwy.

Np. treść nazwy „stół”- jest to mebel, składający się z blatu i nóg, służący do stawiania na nim rzeczy, do pisania.

Desygnatem nazwy „stół” jest przedmiot, który ma konkretne cechy.

Zakresem nazwy „stół' jest zbiór wszystkich istniejących stołów.

Treść nazwy „człowiek” - (jest to zbiór cech, które przypisujemy człowiekowi) jest to istota rozumna, ma wyprostowaną postawę, porusza się na dwóch kończynach dolnych.

Desygnatem nazwy „człowiek” jest każda osoba.

Zakresem nazwy „człowiek” jest zbiór wszystkich ludzi, czyli wszystkich desygnatów.

OSTROŚĆ ZAKRESU NAZWY

Wyróżniamy nazwy ostre i nieostre.

Nieostrość zakresu wiąże się z tym, że niektóre nazwy nie mają wyraźnej treści, to znaczy, iż nawet ten, kto dobrze zna dany język nie umiałby podać takiego zespołu cech, które pozwoliłyby w sposób stanowczy odróżniać desygnaty danej nazwy od innych przedmiotów.

Nazwy stają się nazwami ostrymi dzięki temu, że są nazwami wyraźnymi - to znaczy, umiemy podać zespół cech wystarczających dla odróżnienia desygnatów danej nazwy od innych przedmiotów lub też dzięki temu, że są nazwami dla nas intuicyjnymi - to znaczy, że na podstawie ogólnego wyglądu danego przedmiotu, bez zastanawiania się nad treścią danej nazwy, umiemy określić, czy jest on, czy nie jest desygnatem tej nazwy.

Np. „wysoki człowiek”

Wysocy - to tacy ludzie, którzy mają powyżej 2 m

Nie wysocy- to tacy, którzy mają poniżej 1,50 m

Wzrost średni- tacy, co do których nie wiadomo, czy są, czy nie są wysokimi.

P O D Z I A Ł N A Z W

1. Ze względu na liczbę wyrazów składowych nazwy dzielimy na:

Nazwy proste - są to nazwy składające się tylko z jednego wyrazu np. książka, człowiek, dom.

Nazwy złożone - które składają się przynajmniej z dwóch wyrazów np. wysoki człowiek, zielone drzewo, UMCS.

2. Według tego do czego się odnoszą nazwy dzielimy na:

Konkretne - są to nazwy, które są znakami rzeczy lub osób, ewentualnie czegoś, co sobie jako rzecz lub osobę wyobrażamy. Nazwą konkretną będzie: człowiek, wysoki człowiek, słońce.

Abstrakcyjne - są to nazwy, które nie są znakami rzeczy, czy osób, czy czegoś co sobie jako rzecz lub osobę wyobrażamy. Wskazują one pewne cechy wspólne wielu przedmiotom np. białość, szarość. Na pewne zdarzenie lub stan rzeczy np. cisza, kradzież albo na pewien stosunek zachodzący między przedmiotami np. mniejszość, większość.

3. Według sposobu wskazywania desygnatów nazwy dzielimy na:

Generalne - są to nazwy, które przysługują przedmiotom ze względu na jakieś cechy, które tym przedmiotom przypisują np. człowiek, krzesło, dom, drzewo.

Indywidualne - to nazwy służące do oznaczania poszczególnych tych a nie innych przedmiotów, nie przypisując przez to samo danemu przedmiotowi takich czy innych właściwości, wyróżniających go np. wszystkie imiona własne.

4. Ze względu na ilość desygnatów, nazwy dzielimy na:

Ogólne - które posiadają więcej niż jeden desygnat np. mikrofon, człowiek.

Jednostkowe - są to nazwy, które posiadają jeden desygnat np. słońce.

Puste - które desygnatów nie posiadają, będą to nazwy abstrakcyjne.

np. wszystkie postacie literackie, bohaterowie filmów.

Przykład:

„zamek” - jest to nazwa wieloznaczna, bo może być jako budowla i zamek w drzwiach. My rozpatrujemy zamek jako budowla.

Treść nazwy: budowla.

Desygnat: konkretny zamek.

Zakres: zbiór wszystkich budowli.

Jest to nazwa: prosta, konkretna, generalna, ogólna.

Przykład:

„Wenus” to nazwa wieloznaczna. Może być Wenus jako bogini i Wenus jako planeta.

Wenus - bogini

Desygnat - bogini

Nazwa prosta, konkretna, indywidualna, pusta.

Wenus - planeta

Desygnat - konkretna planeta

Zakres nazwy: jedna planeta

Nazwa: prosta, konkretna, indywidualna, jednostkowa.

Przykład:

Robert Redford

Treść nazwy: mężczyzna, który ma na imię Robert i nazwisko Redford

Desygnat: każdy mężczyzna, który ma na imię Robert i nazwisko Redford

Nazwa: złożona, konkretna, generalna, ogólna.

UWAGA! przy analizie zawsze wychodzić od określenia treści i czy jest to nazwa jednoznaczna, czy wieloznaczna.

RELACJE JAKIE ZACHODZĄ MIĘDZY ZAKRESAMI DWÓCH NAZW.

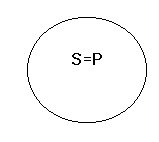
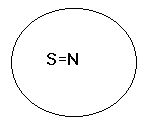
1. Relacja równoważności, czyli zamienności zakresu dwóch nazw.

S i P to są nazwy.

S jest zamienne z P wtedy i tylko wtedy, gdy każde S jest P i każde P jest S.

S

P

Każdy desygnat nazwy S jest jednocześnie desygnatem nazwy P.

np. ziemniak - kartofel

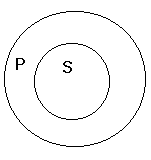
2. Relacja podrzędności zakresu nazwy S względem zakresu nazwy P.

S jest podrzędne względem P wtedy i tylko wtedy, gdy każde S jest P, ale nie każde P jest S.

S

P

Np. wróbel - ptak (każdy wróbel jest ptakiem, ale są ptaki które wróblami nie są.)

3. 
   Relacja nadrzędności zakresu nazwy S względem zakresu nazwy P.

S jest nadrzędne względem P wtedy i tylko wtedy, gdy nie każde S jest P, ale każde P jest S. Np. ptak jest nadrzędny do nazwy wróbel.

P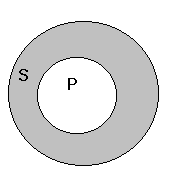

S

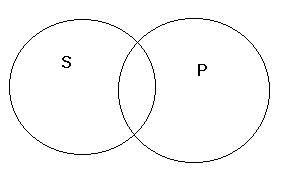
4. Relacja krzyżowania się zakresu nazwy S względem zakresu nazwy P.

S krzyżuje się z P wtedy i tylko wtedy, gdy istnieje S nie będące P, istnieje P nie będące S, i istnieje S będące P.

S

P

Np. polski samochód - niebieski samochód

5. Relacja wykluczania się zakresu nazwy S względem nazwy P

S wyklucza się z P wtedy i tylko wtedy, gdy istnieje S nie będące P, istnieje P nie będące S, ale nie istnieje S będące P.

S

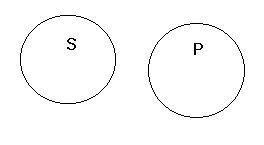
Np. drzewo i samochód.

Przykład:

Odra i rzeka

O R

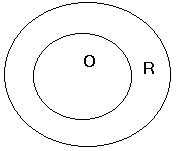
Odra - rzeka polska, to relacja podrzędności.

Odra - jako choroba, to relacja wykluczania się.

Przykład: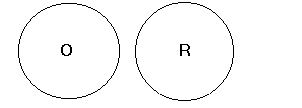

Stały = niezmienny

To relacja równoważności.

DEFINICJE

Słowo definicja pochodzi z jęz. łacińskiego i oznacza odgraniczenie.

Wyróżniamy definicje:

• realne

• nominalne.

Definicjami realnymi -są zdania podające taką charakterystykę pewnego przedmiotu, czy też przedmiotów jakiegoś rodzaju, które tym i tylko tym przedmiotom można przypisać. Są to definicje w języku pierwszego stopnia, czyli w języku opisowym i przedmiotowym.

Definicja realna ma podać te cechy, które są charakterystyczne dla określonego przedmiotu.

Np. książka jest to......

Definicje nominalne - jest to takie wyrażenie, które w ten czy inny sposób podaje informację o znaczeniu jakiegoś słowa czy słów.

Np. nazwa „książka” oznacza.......

Nazwa „wysoki człowiek” oznacza.................

Definicja nominalna podaje informację o znaczeniu definiowanego słowa, jest to wypowiedź drugiego stopnia.

PODZIAŁ DEFINICJI

1. Definicja równościowa ma postać:

Definiendum = definiens

Definiendum - jest to wyraz lub wyrażenie w skład którego wchodzi wyraz czy wyrażenie definiowane, czyli to, którego nie rozumiemy.

Definiens - to wyraz lub wyrażenie wyjaśniające znaczenie wyrazu czy wyrażenia definiowanego, czyli tego, którego nie rozumiemy. Znak równości symbolizuje spójnik definicyjny.

Spójnikami definicyjnymi są najczęściej zwroty: jest, są, jest to, są to, znaczy tyle co, oznacza.

Przykład:

Człowiek jest to istota rozumna.

Definiendum spójnik definiens

definicyjny

2. Definicja nierównościowa - jest to taka definicja, która nie ma postaci definicji równościowej, czyli definiendum nie równa się definiens.

Przykład:

x + y = 12

x - y = 4

x= 8

y = 4

to przykład definicji przez postulaty, czyli definicji nierównościowej.

3. Podział definicji ze względu na budowę definiensa:

• definicje klasyczne

• definicje nieklasyczne

Definicje klasyczne

Przykład:

Człowiek jest to istota rozumna.

A B C

Definicja klasyczna ma postać: A jest B mające cechę C.

Przy czym:

duża literka A oznacza wyraz definiowany,

duża literka B- rodzaj, czyli pojęcie bardziej ogólne od pojęcia definiowanego A

duża literka C - różnica gatunkowa, czyli ta cecha, która pozwala ograniczyć zakres szerszy, czyli tą część która nas interesuje.

Definicja klasyczna nazywana jest też definicją przez rodzaj i różnice gatunkowe.

Przykłady definicji klasycznych:

Kwadrat jest to prostokąt równoboczny.

A B C

Zbożem nazywa się rośliny uprawne z rodziny traw dostarczające ziarna i słomę

A B C

Definicje nieklasyczne - są to takie definicje, które nie posiadają postaci definicji klasycznych. np. Zbożem nazywamy pszenicę, żyto, owies itd.

Jest to definicja przez wyliczanie.

4. Ze względu na budowę definiendum definicje dzielimy na:

• wyraźne

• kontekstowe

Definicje wyraźne są to definicje w których wyrażenie definiowane występuje samo bez żadnego kontekstu.

Np. Człowiek jest to istota rozumna.

Książka to zbiór zapisanych, zszytych kartek, posiadająca oprawę.

Definicja kontekstowa -zawiera nie sam wyraz czy wyrażenie definiowane, ale typowy kontekst w którym wyrażenie czy wyraz definiowany występuje.

Np. Szerokość geograficzna punktu jest to kąt zawarty pomiędzy promieniem przechodzącym przez dany punkt ziemi a płaszczyzną równika ziemskiego.

Np. Logarytmem liczby A przy podstawie B nazywamy wykładnik potęgi, do której należy podnieść liczbę B aby otrzymać liczbę A.

5. Ze względu na zadania definicje dzielimy na:

• Sprawozdawcze

• Projektujące

Definicje sprawozdawcze są to takie definicje, które wskazują jakie znaczenie ma lub miał wyraz definiowany kiedyś w pewnym języku.

np. kwadrat, logarytm, komputer.

Definicje sprawozdawcze możemy oceniać według kategorii prawdziwości i fałszywości.

Definicje projektujące - są to definicje które ustalają znaczenie wyrazu lub wyrażenia na przyszłość. np. Kierownika suwnicy elektrycznej nazywać się będzie w niniejszej ustawie „suwnicowym”.

Wśród wyrażeń projektowych wyróżniamy:

1. Definicje konstrukcyjne - ustalają znaczenie nowego wyrazu lub wyrażenia na przyszłość lub nadają zupełnie nowe znaczenie wyrazowi już istniejącemu.

Definicja konstrukcyjna jest nam potrzebna zwłaszcza wtedy, kiedy zjawia się potrzeba wprowadzenia nowego wyrazu czy wyrażenia do języka, np. gdy wystąpiło nowe zjawisko społeczne, wymyślono nową maszynę, którą niewygodnie byłoby określać za pomocą długiego opisu. Np. zamiast mówić o żłobkach, do których rodzice mogą oddawać dzieci na cały tydzień z wyjątkiem dnia wolnych od pracy, lepiej jest wprowadzić nową nazwę złożoną: „żłobek tygodniowy”.

2. Definicje regulujące - ustalają na przyszłość wyraźne znaczenie istniejącego wyrazu licząc się bardzo z jego dotychczasowym znaczeniem.

Definicjami regulującymi są najczęściej definicje napotykane w ustawach.

Np. „Przyuczoną pielęgniarką w rozumieniu niniejszej ustawy jest osoba, która bez przygotowania teoretycznego wykonywała w zakładach zamkniętych służby zdrowia funkcje pielęgniarskie w okresie co najmniej dwóch lat”. Wyrażenie „przyuczona pielęgniarka” zostało dokładnie sprecyzowane przez ustawodawcę, chociaż było wcześniej używane.

WARUNKI POPRAWNOŚCI DEFINIOWANIA

1. Definicja musi być prawdziwa.

2. Definicja musi być informacyjna. (użyte zwroty zrozumiałe)

3. Definicja musi być ekonomiczna. (minimum słów a maksimum myśli)

BŁĘDY DEFINIOWANIA - czyli te które najczęściej występują:

1. Błąd zwany „nieznane przez nieznane” - (wyjaśniamy coś nieznanego używając zwrotów znanych)

2. Błąd zwany „błędne koło bezpośrednie” - ( gdy wyraz czy wyrażenie definiowane występuje i w definiendum i w definiensie) np. masło maślane.

3. Błąd zwany „błędne koło pośrednie” - np. definiujemy pojęcie A przez pojęcie A.

A jest B

B jest C

C jest A

4. Definicja może być albo za wąska albo za szeroka

Definicja jest za wąska, kiedy zakres definiensa nie obejmuje wszystkich przedmiotów należących do zakresu definiendum.

Np. „Zwykły ołówek to przyrząd do pisania złożony z pręcika grafitu umieszczonego w niebieskiej oprawce z cedrowego drzewa”.

Zbyt bogatą podano tu treść, a więc za wąski jest zakres definiensa. Nie obejmuje on ołówków polakierowanych na żółto, na czarno, na zielono, które też są nazwane ołówkami.

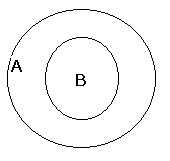
Definicja będzie za szeroka, kiedy zakres definiensa obejmuje także jakieś przedmioty nie należące do zakresu definiendum.

Przykład: „Prokurator jest to pracownik prokuratury”. Zakres definiensa „pracownik prokuratury” jest nadrzędny w stosunku do zakresu definiendum, jako że do pracowników prokuratury należą także oprócz prokuratorów woźni i sprzątaczki prokuratury, którzy przecież prokuratorami nie są.

5

30

nadrzędności

nadrzędności

P

---