Badania operacyjne (część 2)

• Teoria grafów

• Metody sieciowe (oparte na teorii grafów)

• metoda ścieżki krytycznej,

• metoda PERT.

Teoria grafów

• X - zbiór wierzchołków grafu - punktów przestrzeni, w której rozpięty jest graf.

• R - łuki grafu - zbiór skierowanych relacji w grafie.

• G=(X, R) - graf skierowany nieobciążony - będący połączeniem wierzchołków łukami.

• f₁, ... , f_n - obciążenia grafu - zbiór n funkcji opisujących własności wierzchołków i łuków grafu

• G*=(X, R, f₁, ... , f_n) - graf skierowany obciążony (sieć).

• Długość łuku - liczba przyporządkowana danemu łukowi, może być różna dla obu kierunków (od A do B i od B do A).

• Graf zwarty - graf, w którym między każdą parą wierzchołków istnieje ścieżka.

• Długość ścieżki - suma liczb długości łuków tworzących daną ścieżkę.

• Odległość dwóch wierzchołków grafu zwartego - długość najkrótszej ścieżki łączącej te wierzchołki.

• Sieć - graf skierowany obciążony.

Zagadnienie 7 mostów Królewca

• W 1736 roku Królewiec odwiedził szwajcarski matematyk Leonard Euler (1707-1783). Przedstawiono mu zagadnienie, które od dawna nurtowało mieszkańców:

Czy możliwą jest taka przechadzka po mieście by powrócić do punktu początkowego, przechodząc po każdym z 7 mostów jednokrotnie?

• Euler udowodnił, że wymagałoby to wybudowania dwóch dodatkowych mostów.

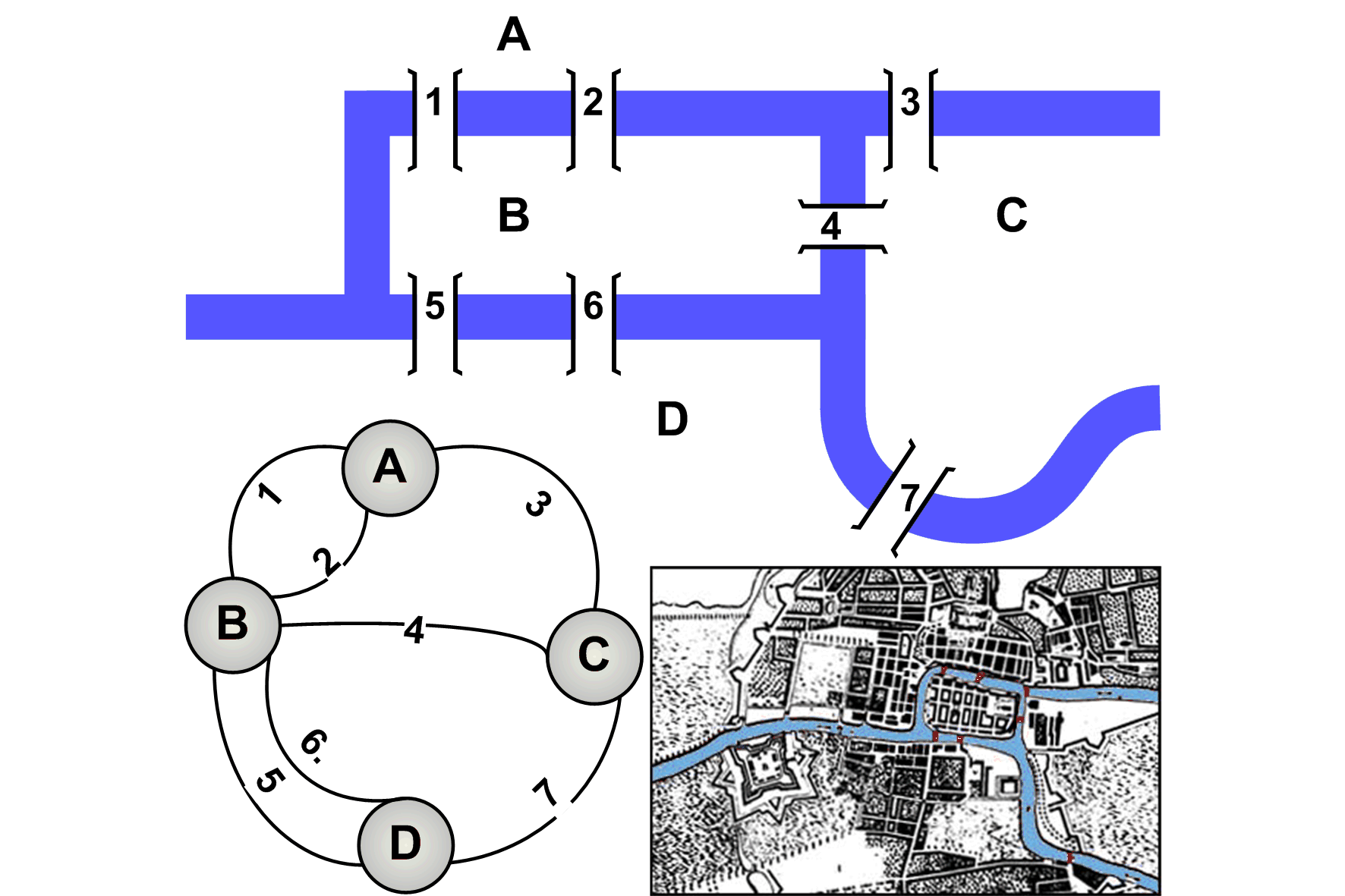
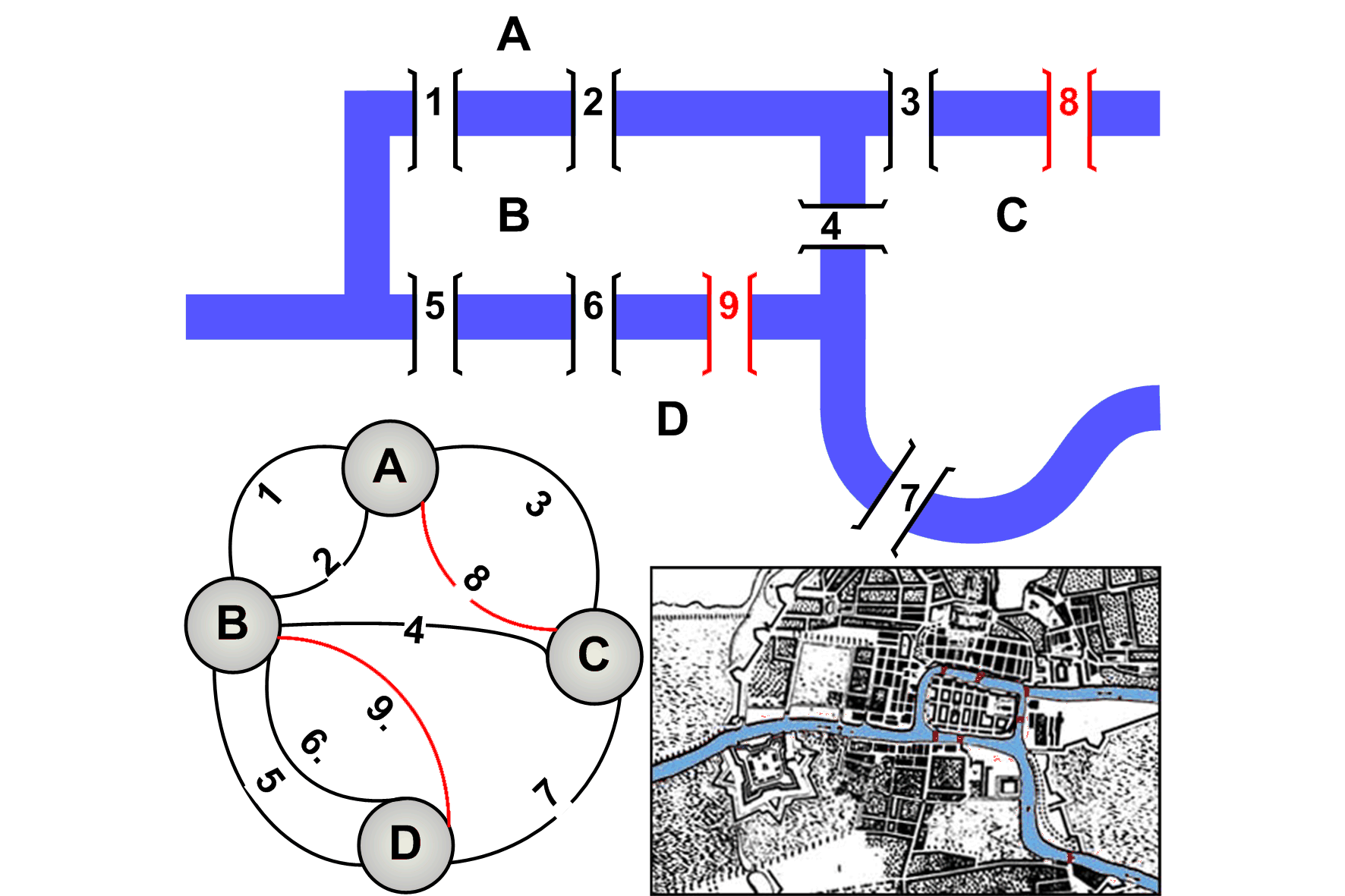
• Euler uogólnił rozważany przypadek, podając warunki konieczne dla przypadku tak zwanego `cyklu eulerowskiego':

• graf musi być zwartym,

• liczba łuków odchodzących z każdego węzła musi być parzysta (w przeciwnym razie nie jest możliwe wejście i wyjście po różnych mostach).

Grafy

• Różne konwencje przedstawiania grafów (tabele, postacie graficzne)

Tabela definiująca graf

Teoria grafów

• Stopnie sieci:

• pierwszy - w którym czynności reprezentowane są przez wierzchołki a zdarzenia przez łuki,

• drugi - w którym czynności reprezentowane są przez łuki a zdarzenia przez wierzchołki,

• trzeci - w których wierzchołki mogą reprezentować zarówno zdarzenia jak i czynności, a łuki - następstwa w czasie.

Najczęściej wykorzystywane w praktyce są sieci drugiego stopnia. Ich obciążenia mogą być deterministyczne (jednoznacznie określone) lub probabilistyczne (znane z określonym prawdopodobieństwem).

CPM

• Metoda ścieżki krytycznej, metoda CPM (ang: critical path method) - odwzorowuje w formie zwartego grafu skierowanego i obciążonego zależności (technologiczne, produkcyjne, organizacyjne) między poszczególnymi czynnościami składowymi, powiązanie między nimi, pokazuje zależności między wykonaniem poszczególnych czynności, wpływ terminów wykonania na ich koszt oraz nakłady na całe przedsięwzięcie. Metoda polega na wyznaczeniu najdłuższej ścieżki łączącej wierzchołek początkowy z końcowym.

PERT

• Metoda PERT (ang: program evaluation and review technique) - poza wyznaczeniem ścieżki krytycznej pozwala na statystyczne oszacowanie czasu trwania określonych czynności, kosztów lub prawdopodobieństwa awarii. Pozwala więc na wyznaczenie prawdopodobieństwa realizacji poszczególnych etapów przedsięwzięcia w określonych terminach.

Liczby przyporządkowane poszczególnym łukom oblicza się z wzoru:

t_i = (a + 4m + b) / 6

gdzie:

• a - optymistyczny czas trwania (koszt, ryzyko) czynności,

• m - najbardziej prawdopodobny czas trwania (koszt, ryzyko) czynności,

• b - pesymistyczny czas realizacji (koszt, ryzyko) czynności.

Następnie wyznacza się ścieżkę krytyczną przy wykorzystaniu średnich czasów trwania (kosztów, ryzyka) poszczególnych czynności.

Oblicza się odchylenia standardowe * czasów (kosztów, ryzyka) poszczególnych czynności według wzoru:

*_ti = (b - a) / 6

Na podstawie znajomości odchyleń standardowych * poszczególnych czynności można określić wartość zmiennej pomocniczej

Z = (D_t - W_t) / * *_ti

gdzie:

• D_t- dyrektywny czas (koszt, stopień ryzyka) całego przedsięwzięcia,

• W_t- wyznaczony ze ścieżki krytycznej najwcześniejszy termin (koszt, najmniejsze ryzyko) realizacji całości zagadnienia,

• t_i- odchylenie standardowe spodziewanego terminu realizacji (kosztu, poziomu ryzyka) przedsięwzięcia, obliczone z sumy odchyleń standardowych wzdłuż ścieżki krytycznej.

Z tablic dystrybuanty rozkładu normalnego można następnie obliczyć prawdopodobieństwo P(Z) zrealizowania przedsięwzięcia w zadanym terminie D_t (przy zadanym koszcie całkowitym, stopniu ryzyka, itp).

A, 1, B,

B, 5, D,

D, 6, B,

B, 4, C,

C, 8, A,

A, 3, C,

C, 7, D,

D, 9, B,

B, 2, A.

Czynność

Zdarzenie

Czas

początkowe

końcowe

realizacji

A

B

C

D

E

F

G

H

I

J

K

L

1

1

1

2

2

2

3

3

4

4

5

6

2

3

4

3

5

6

5

6

5

6

7

7

102.5

105.0

70.8

85.7

99.7

90.5

108.7

109.3

101.3

92.2

90.2

92.2

---