Badania operacyjne (część 4)

• Metody obliczeniowe zagadnienia minimalizacji

Zagadnienie optymalizacyjne

• Funkcja celu (kryterium decyzyjne)

f(x) = f(x₁, x₂, … , x_n)

• Zmienne decyzyjne (wielkości optymalizowane)

x_j (j=1, 2, … , n)

• Ograniczenia, warunki ograniczające (funkcja nakładów)

V_i(x) = V_i(x₁, x₂, … , x_n) (i=1, 2, … , m) (warunki uboczne).

• Funkcje celu i nakładów są ciągłe i różniczkowalne (posiadają ciągłe pochodne cząstkowe pierwszego i drugiego rzędu) i są określone na n-wymiarowym wektorze x o nieujemnych składowych

x
0 (warunki brzegowe)

• Zadanie optymalizacyjne polega na wyznaczeniu ekstremum (maksimum lub minimum) funkcji celu przy zadanych ograniczeniach.

• Zadanie optymalizacyjne ma rozwiązanie jeśli nie jest wewnętrznie sprzeczne (zbiór rozwiązań dopuszczalnych nie jest zbiorem pustym) oraz gdy m
  n.

Ekstremum funkcji n zmiennych

• Funkcja celu - f(x) = f(x₁, x₂, … , x_n)

• Gradient funkcji celu w punkcie
  

• Jakobian funkcji f (o m wartościach wektorowych) -

Hesjan funkcji f(x) w punkcie

• Forma kwadratowa -

\

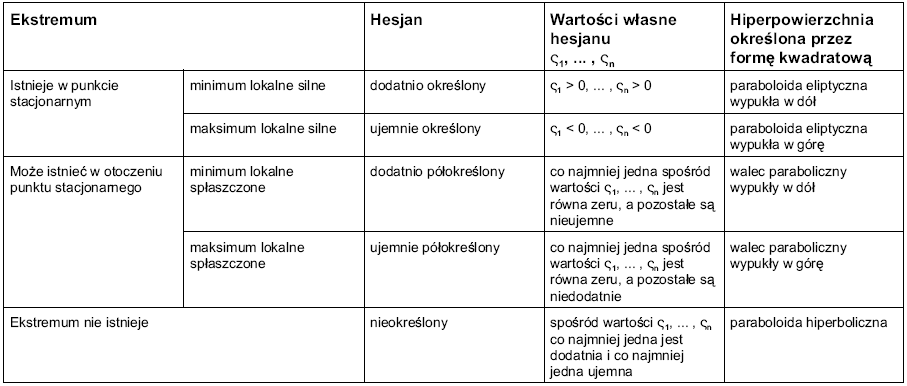
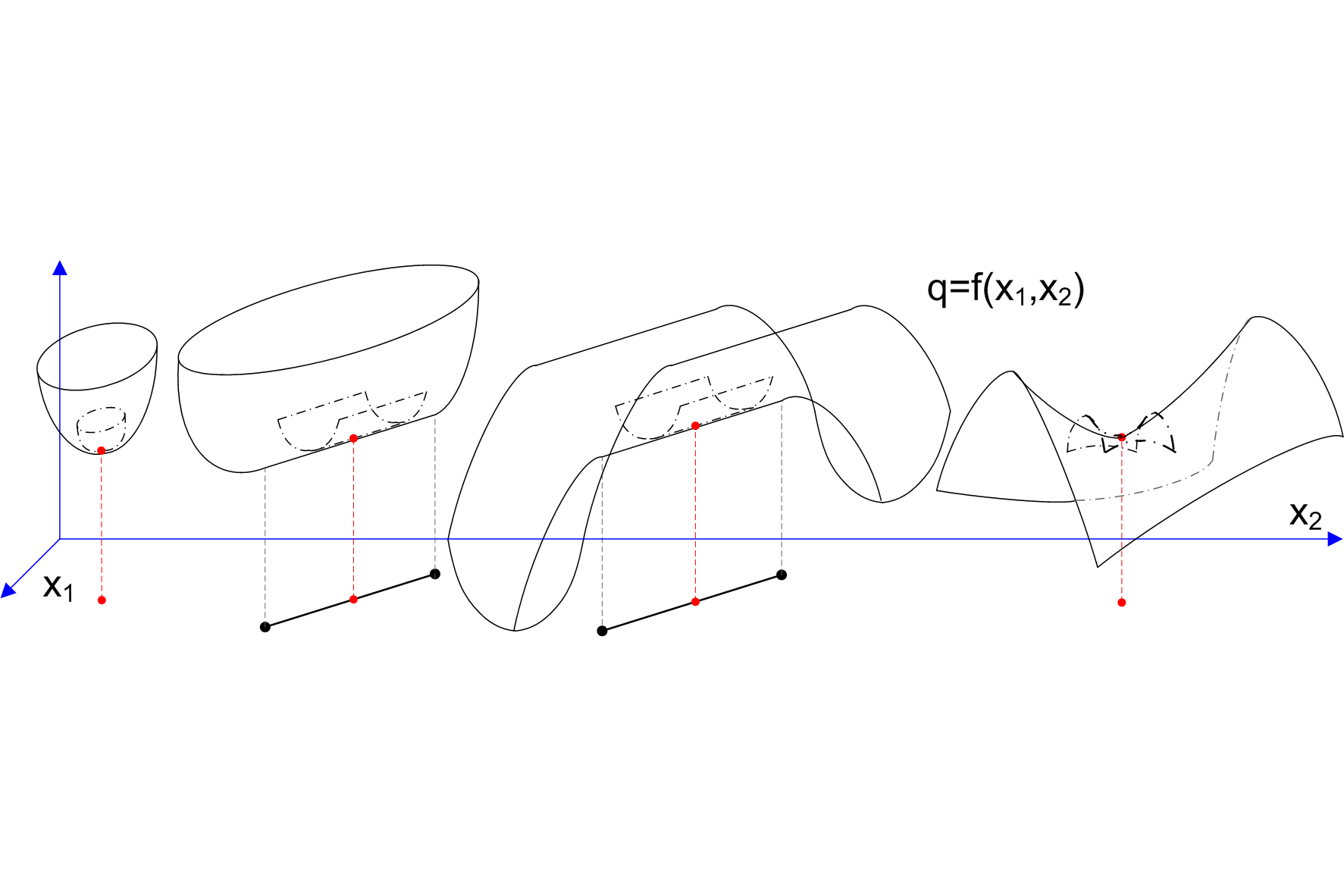
Metody obliczeniowe optymalizacji

• Metody rzędu zerowego, nie korzystające w sposób jawny z pochodnych funkcji kryterium (np. metoda sympleksu)

• wady: niezwykle wolna zbieżność do rozwiązania.

• Metody gradientowe (np. gradientu prostego)

• zalety: zbieżność globalna, niewygórowane wymagania wobec postaci funkcji kryterium f(x), prostota algorytmu,

• wady: wolna zbieżność, konieczność wyboru długości kroku wzdłuż kierunku gradientu.

• Metody rzędu drugiego (newtonowskie)

• zalety: szybka zbieżność,

• wady: wymagania wobec postaci funkcji kryterium, złożoność obliczeniowa, trudności z obliczeniem macierzy drugich pochodnych.

• Metody quasi-newtonowskie (przybliżające wartość hesjanu przy pomocy jakobianu).

Sympleks

• Algorytm rozwiązywania zagadnień optymalizacji, tworzący zbiór bazowych rozwiązań dopuszczalnych - zbieżny do rozwiązania zagadnienia optymalizacji.

• Sympleks - n-wymiarowy wielościan wypukły o n+1 wierzchołkach. W przestrzeni jednowymiarowej (na prostej) sympleks jest odcinkiem, na płaszczyźnie dwuwymiarowej - trójkątem, w trójwymiarowej - czworościanem, itd. Brzegi sympleksu (powierzchnie boczne) są sympleksami niższych wymiarów.

• Dla n+1 punktów wierzchołkowych x₀, x₁, … , x_n zostają obliczone wartości funkcji kryterium f(x₀), f(x₁), … f(x_n). Konstrukcja kolejnego sympleksu polega na odrzutowaniu punktu x_j najbardziej odbiegającego od założonego kierunku poszukiwania ekstremum, względem płaszczyzny przeciwległej powierzchni bocznej.

• Przy zbliżeniu się do ekstremum zostaje zmniejszona wielkość sympleksu, przy braku postępów optymalizacji - jego wielkość jest powiększana.

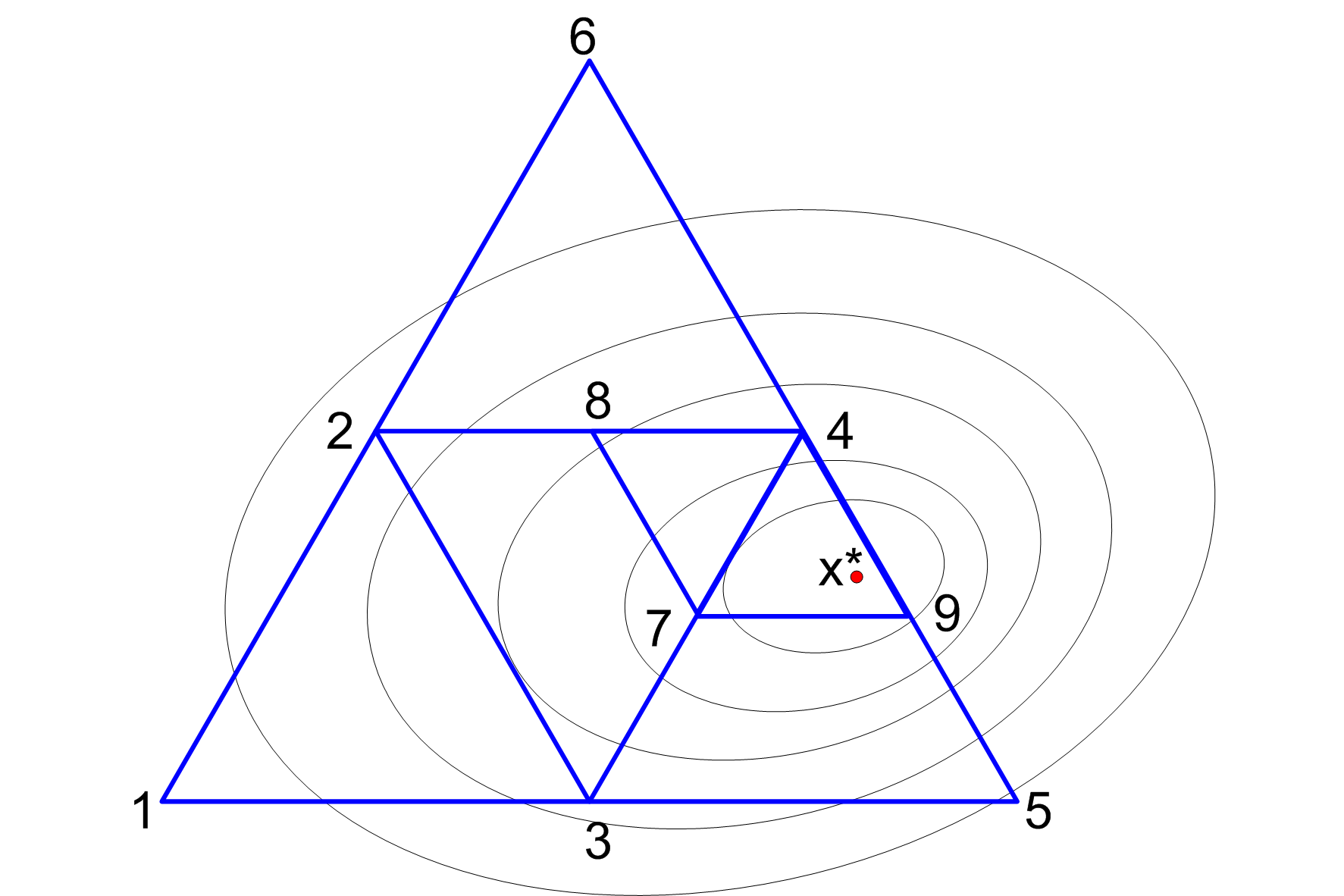
Metoda kierunków sprzężonych Powella

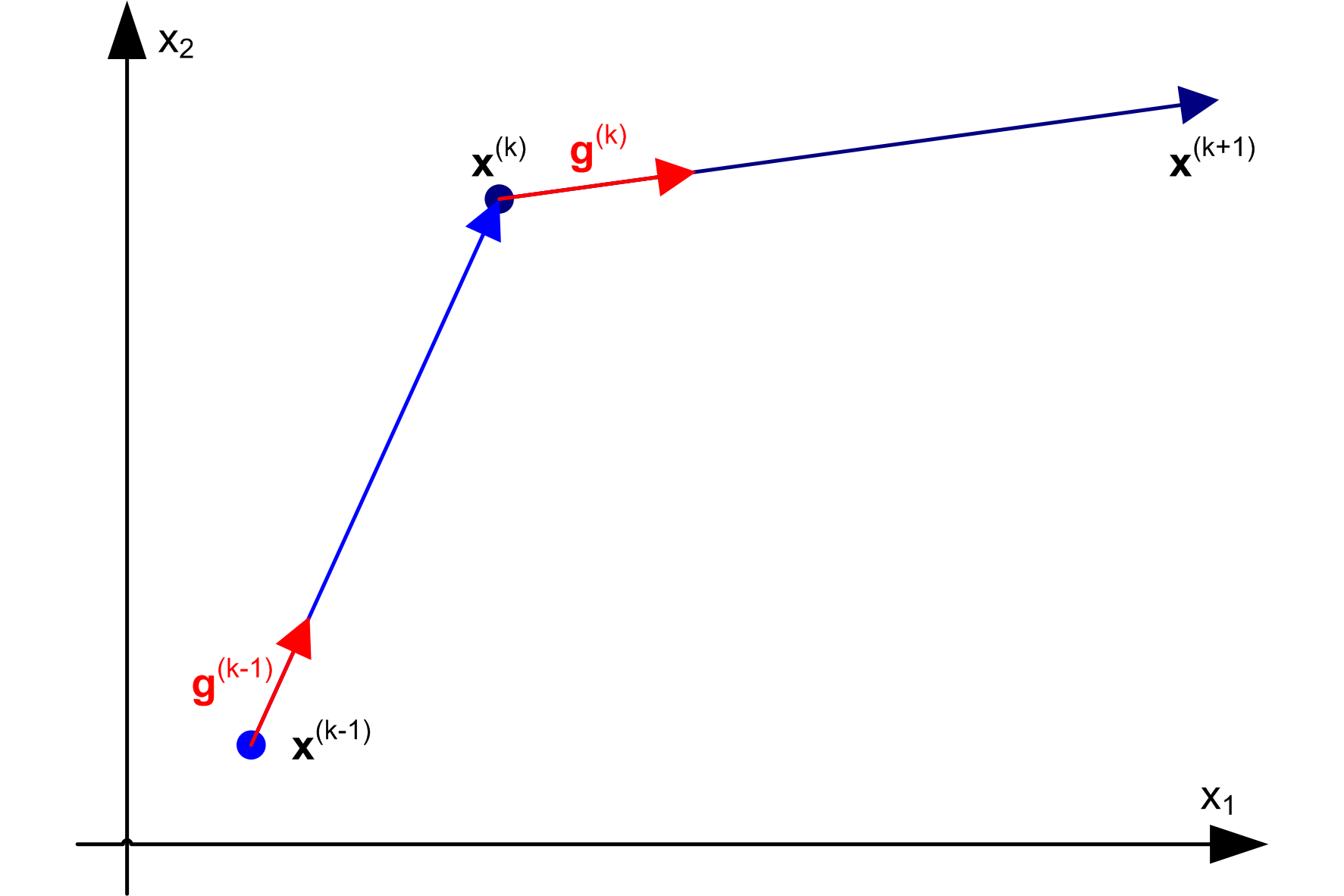
• Aproksymacja w otoczeniu punktu x wartości funkcji kryterium f(x) szeregiem Taylora

f(x) = f(x_k) + *f(x_k) [x - x_k]^T + ½ [x - x_k] *²f(x_k) [x - x_k]^T + R(x)

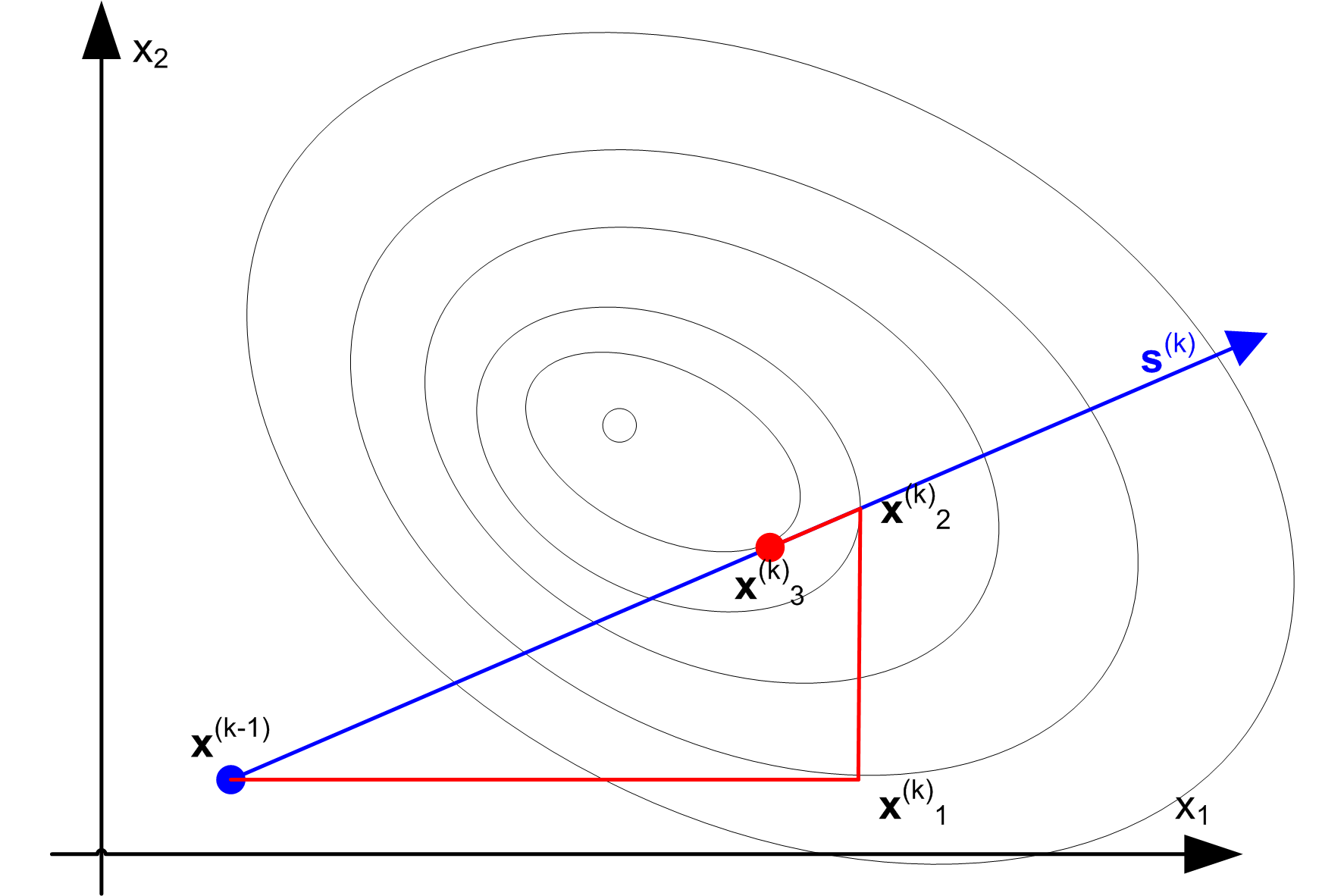
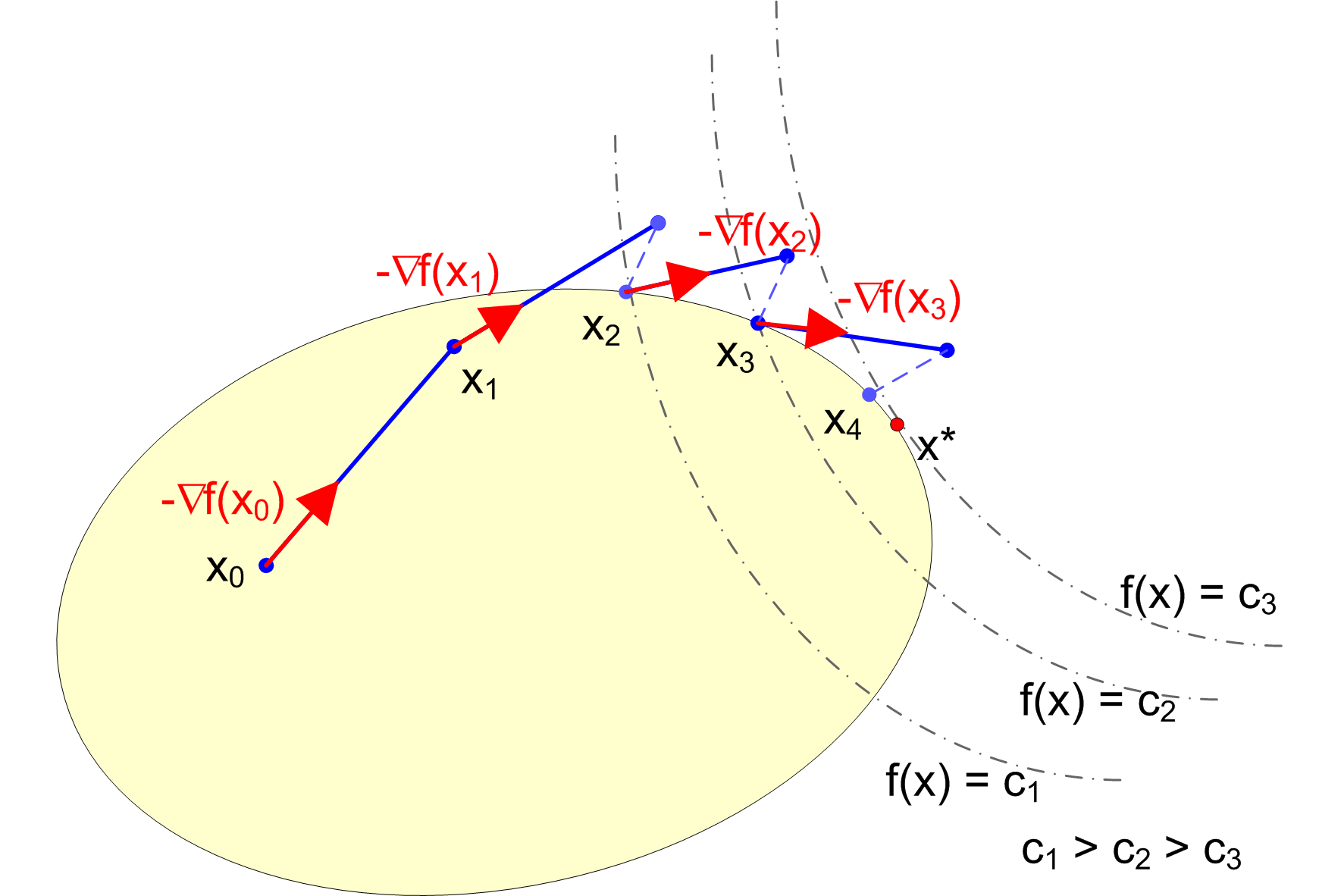
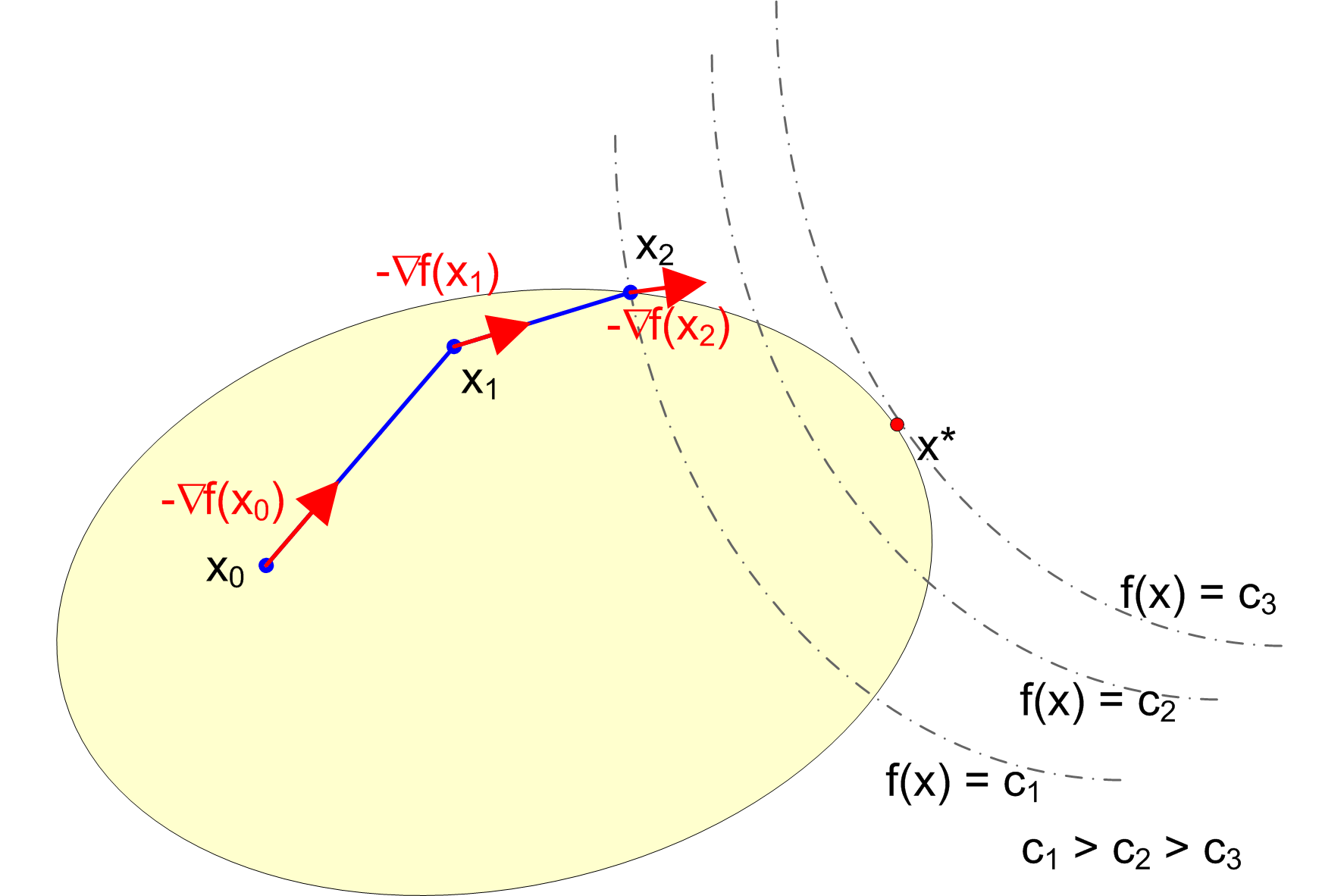
Metoda gradientu prostego

• Metoda gradientu prostego

x_k+1 = x_k -
_k*f(x_k)

_k - długość kroku, dobierana podczas minimalizacji funkcji kryterium wzdłuż kierunku gradientu.

• Wady:

• niezbyt wysoka (w porównaniu z metodami drugiego rzędu) efektywność

• 
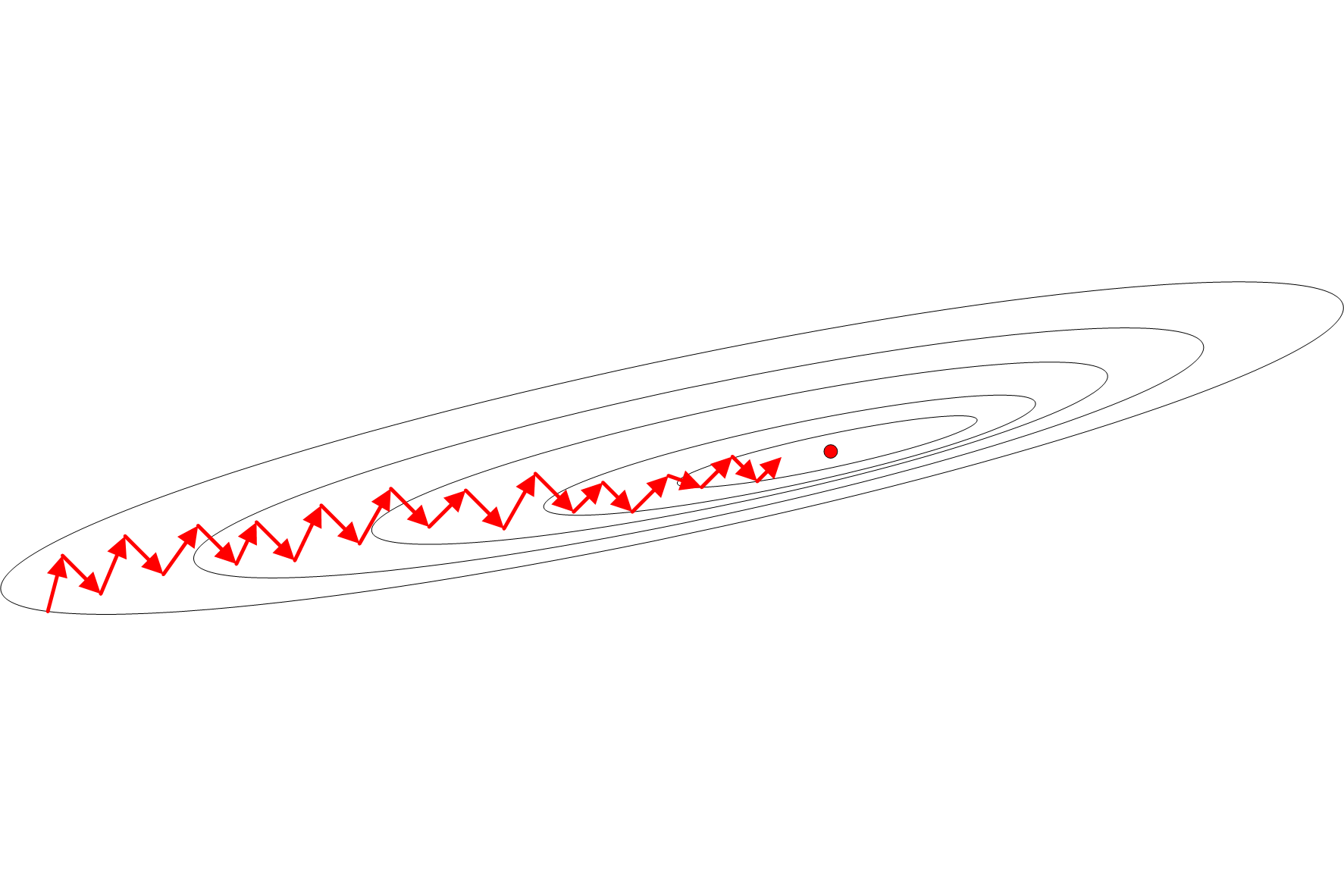
  `zygzakowanie' w przypadku funkcji o wyciągniętych poziomicach.

Metoda Newtona

• Iteracyjna metoda optymalizacji drugiego rzędu

x_k+1 = x_k+1 -
_k*f(x_k) H^-1 (x_k)^T

_k - długość kroku, dobierana podczas minimalizacji funkcji kryterium wzdłuż kierunku gradientu.

Metody quasi-newtonowskie

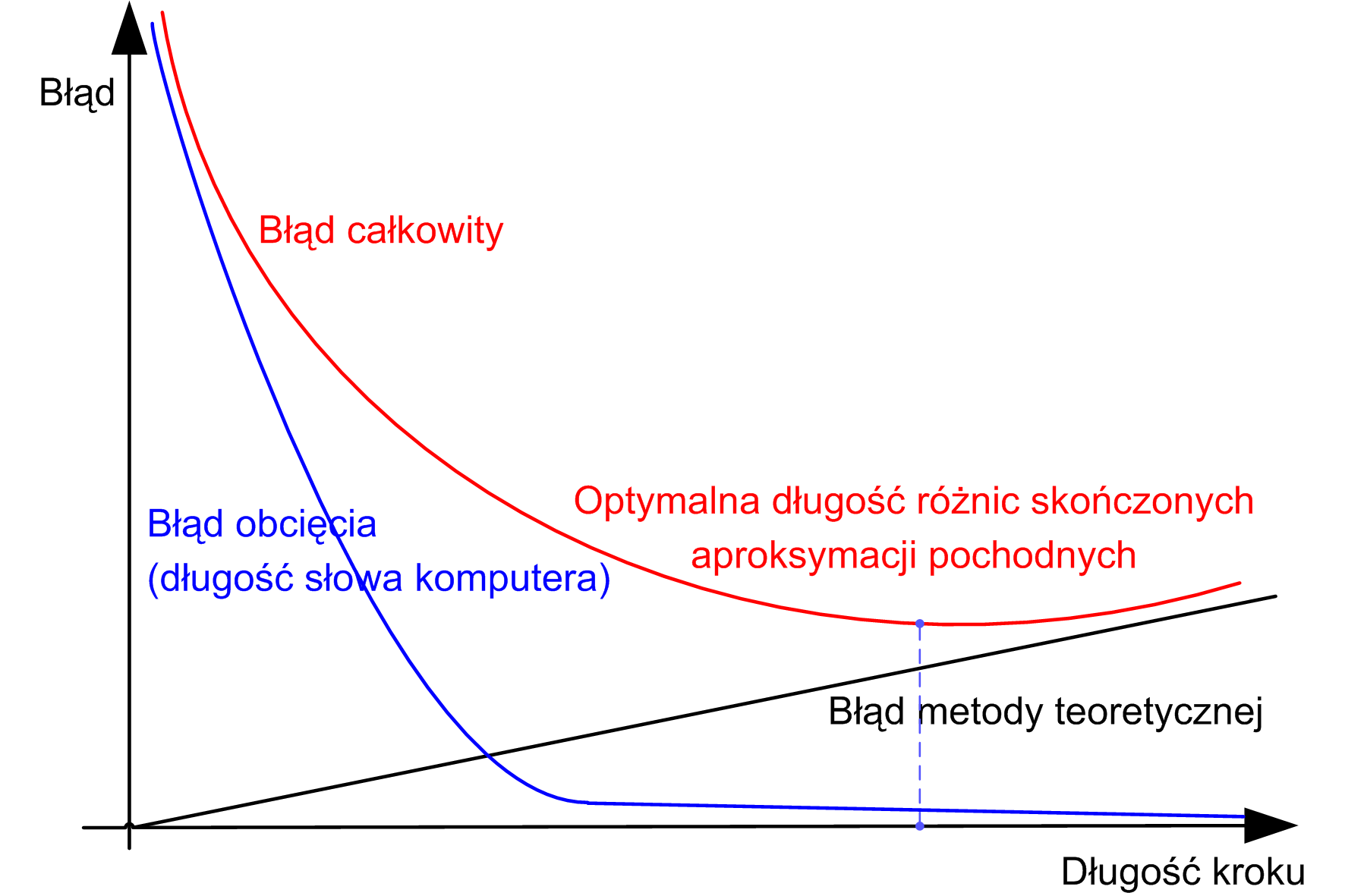
• Konieczność zastąpienia hesjanu aproksymacją jakobianem (macierzą pierwszych pochodnych funkcji kryterium). Potrzeba ta wynika z ogromnego wpływu stosowania różnic skończonych do aproksymacji drugich pochodnych.

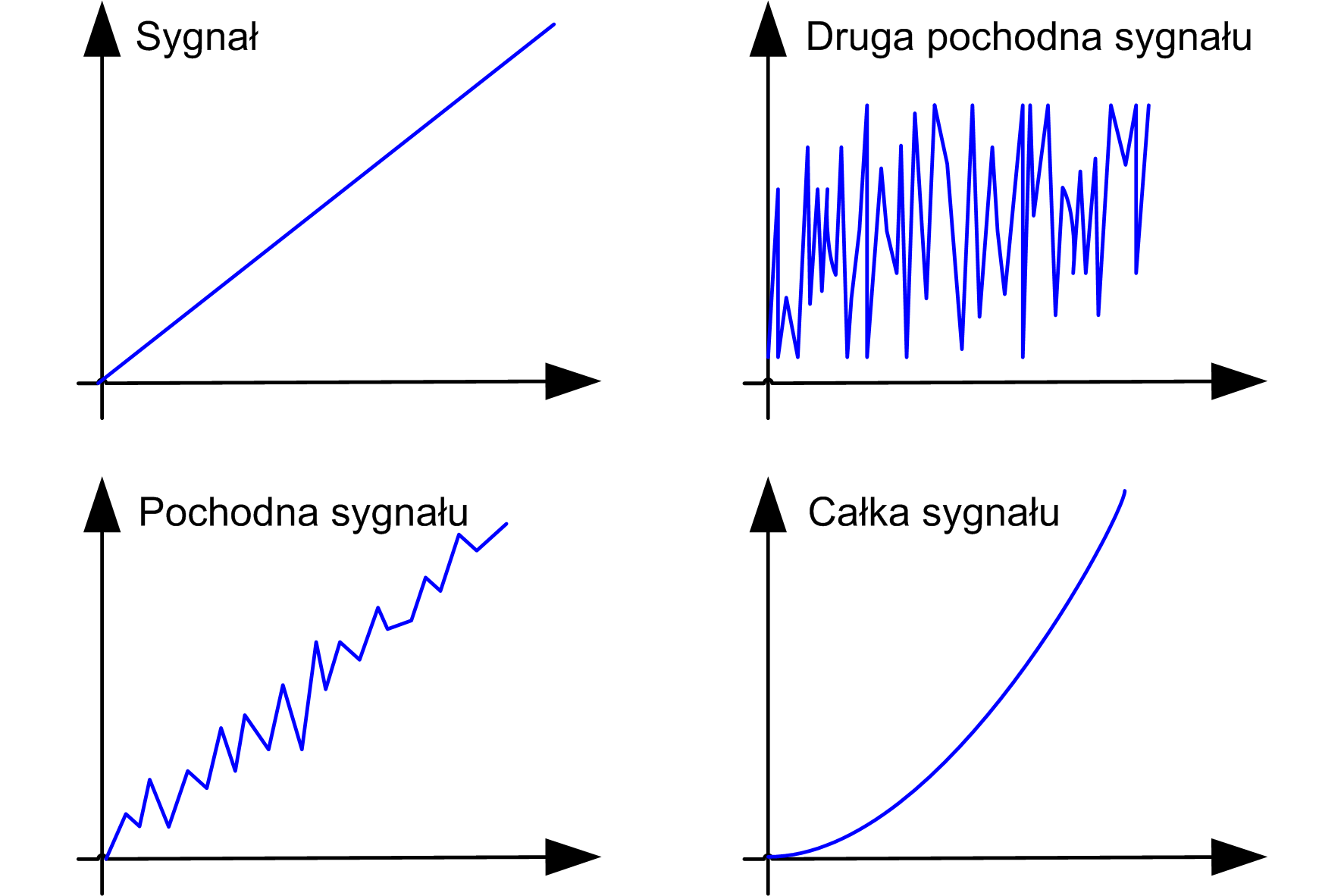
• Aproksymacja pochodnych różnicami skończonymi

Różnice skończone

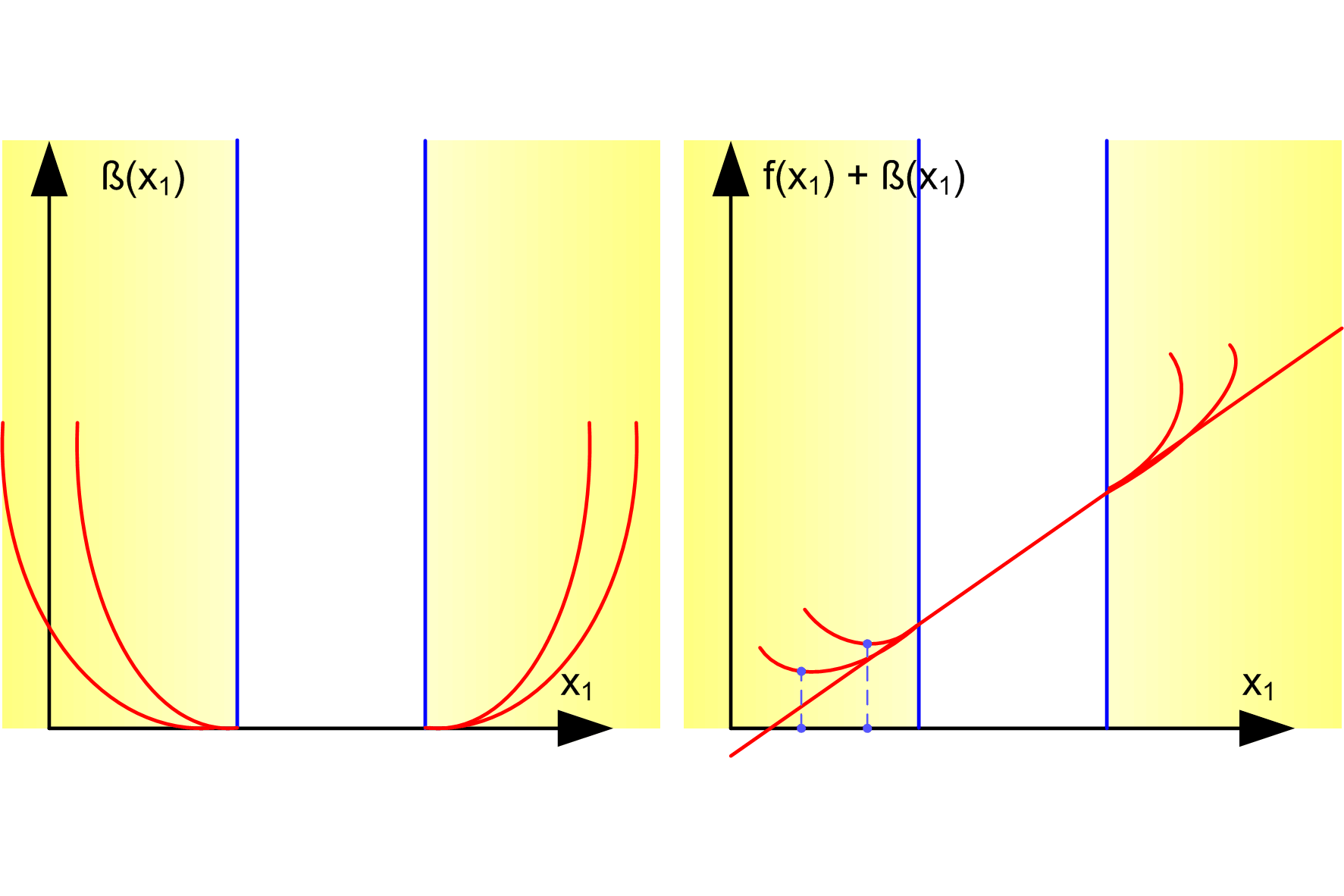
Metody kary wewnętrznej i barier

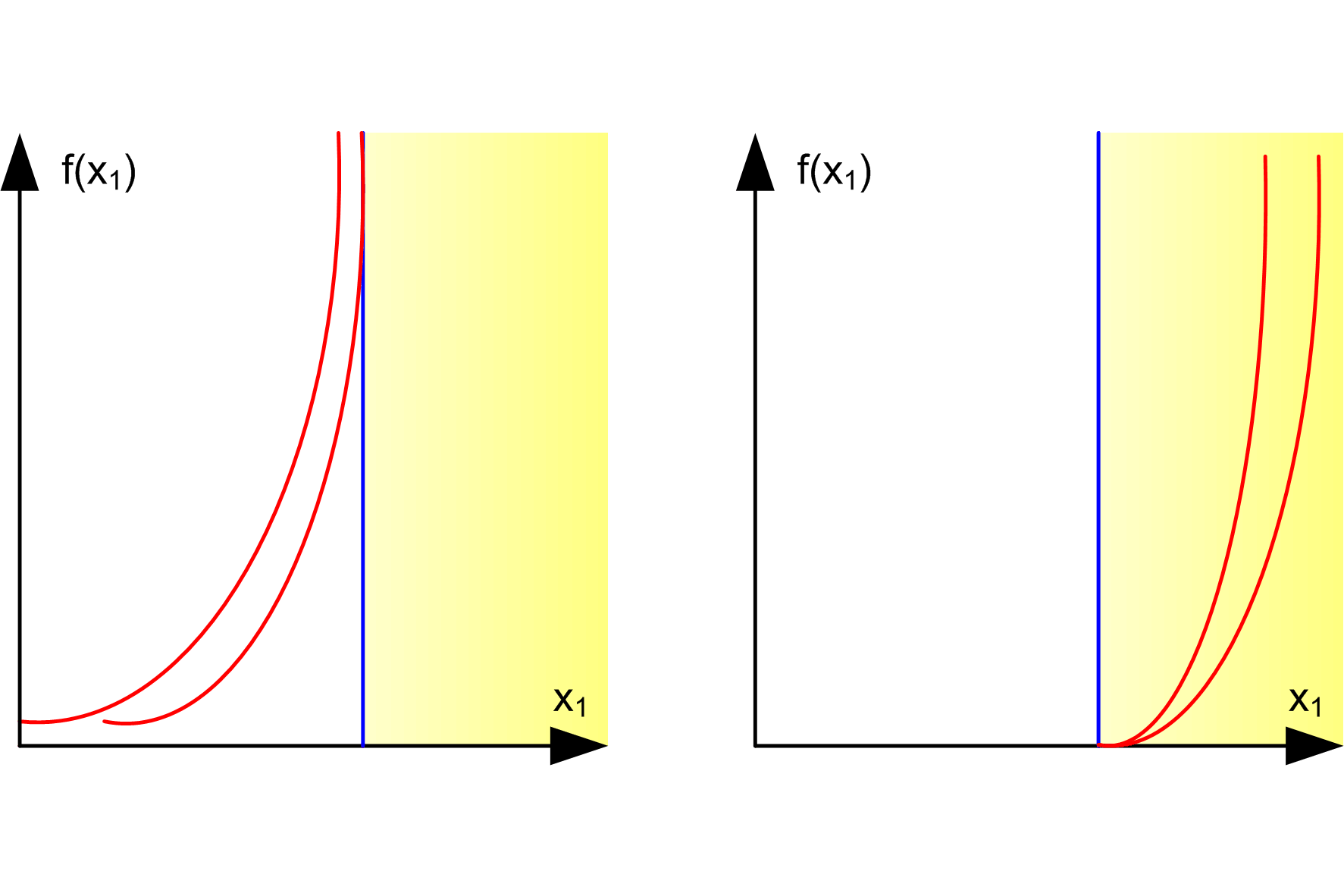
Metody zewnętrznych barier

Metoda rzutowania gradientu (B.Rosena)

Metoda redukcji gradientu

Trudności

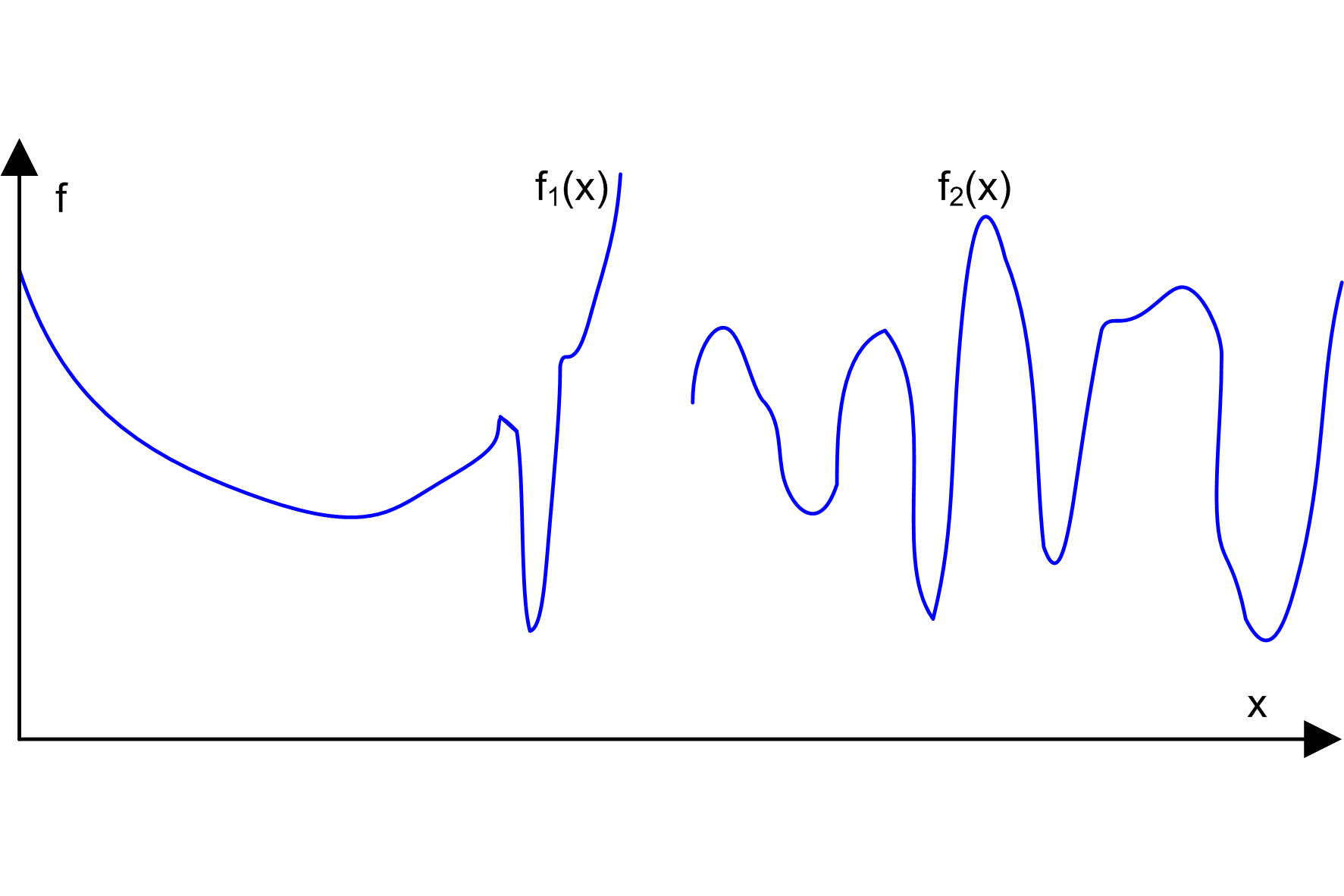
Funkcje trudne do optymalizacji

Porównywanie metod

• Zagadnienia testowe

• Funkcja Rosenbrocka („dolina bananowa”)

f(x) = 100 (x₂ - x₁²)² + (1 - x₁)²

x⁰ = (- 1.2; 1), x* = (1; 1), f* = 0

• Funkcja Powella

f(x) = (x₁ + 10 x₂)² + 5 (x₃ - x₄)² + (x₂ - 2x₃)⁴ + 10 (x₁ - x₄)⁴

x⁰ = (3; - 1; 0; 1), x* = (0; 0; 0; 0), f* = 0

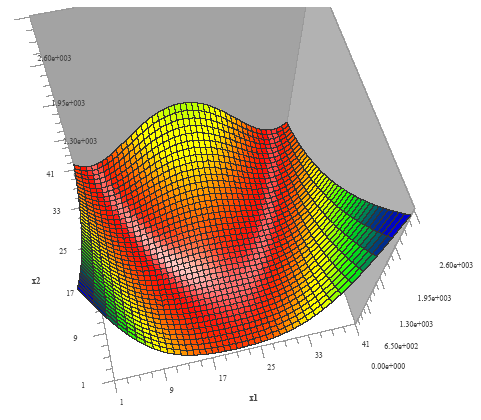
Funkcja Rosenbrocka („dolina bananowa”)

f(x) = 100 (x₂ - x₁²)² + (1 - x₁)²

x⁰ = (- 1.2; 1), x* = (1; 1), f* = 0

Wąska dolina o stromych zboczach i niewielkim spadku dna, zakrzywiona

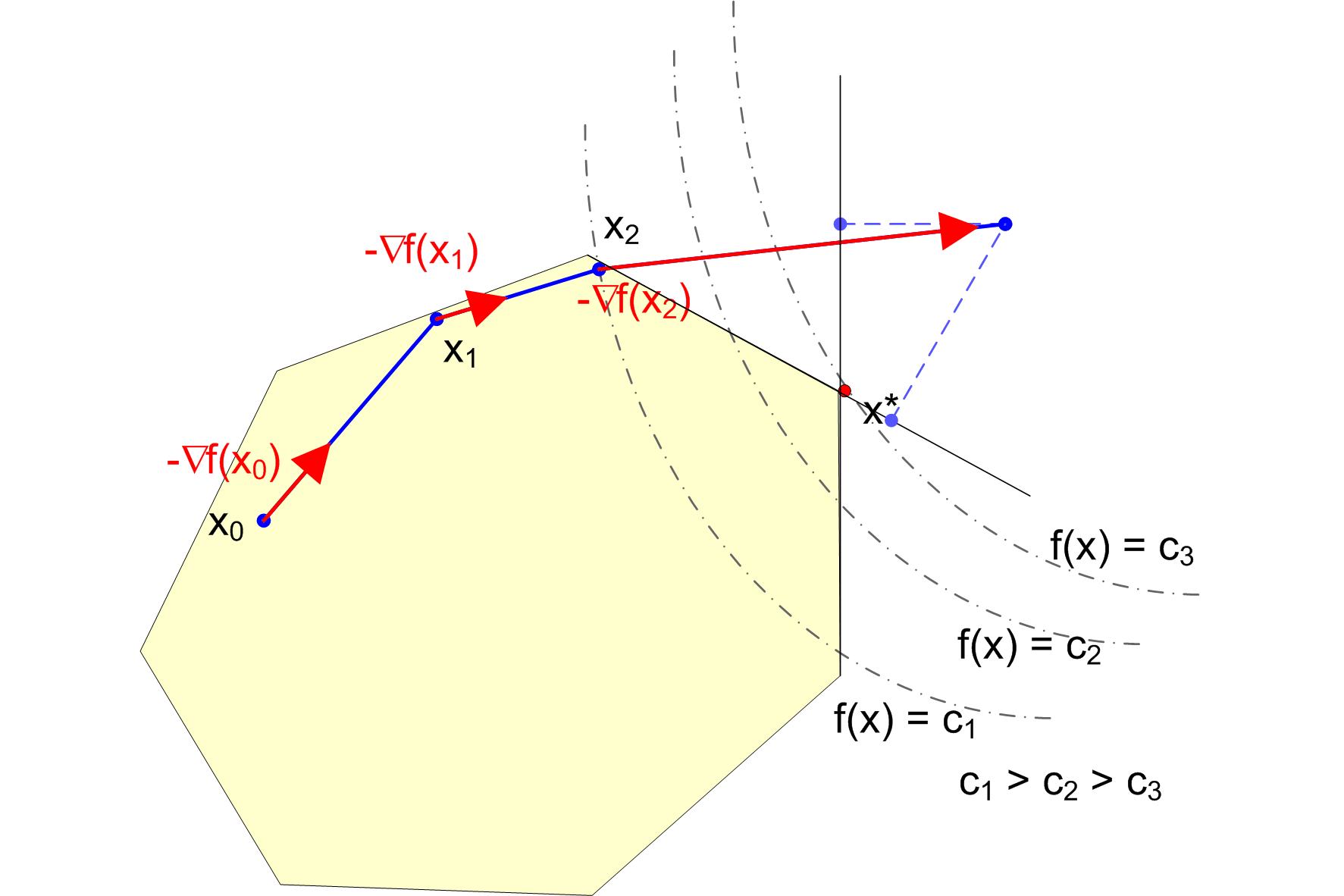
Gradientowe metody obliczeniowe optymalizacji:

- wyznaczenie kierunku,

- minimalizacja funkcji wzdłuż wyznaczonego kierunku.

---