Badania operacyjne (część 1)

• Historia badań operacyjnych

• Pojęcia podstawowe badań operacyjnych

• Teoria modelowania

Historia badań operacyjnych

Wieloaspektowość zagadnienia badań operacyjnych jest przyczyną trudności w ich jednoznacznym zaszufladkowaniu. Badania te wniosły ogromny wkład w rozwój naukowej organizacji pracy, choć autorzy tych koncepcji nie byli specjalistami w tej dziedzinie. Są też przykładem wykorzystania nauki dla celów wojskowych, choć największy wpływ wywarły na ekonomię a ich twórcy zamiast mundurów nosili tweedowe marynarki. Okazały się wreszcie jednym z najistotniejszych elementów przygotowania naukowców i społeczeństwa na przyjęcie teorii systemów i cybernetyki, choć ich czysto aplikacyjny charakter wyraźnie odbiega od graniczących z filozofią zagadnień samo organizacji, samodzielnego życia czy ewolucji systemów.

Wykorzystania nauki do rozwiązania zagadnień praktycznych:

• wyznaczenie przez Archimedesa ilości złota w koronie Hierona II z Syrakuz,

• stworzenie podstaw naukowych rewolucji przemysłowej,

• gospodarka wiedzą jako podstawa rozwoju cywilizacji postindustrialnej.

Z drugiej strony - wykorzystanie nauki do celów wojskowych:

• wynalazki wojskowe starożytności, rozwój balistyki,

• wojskowość Napoleona oparta na metodach matematycznych,

• gry wojenne, wojny cybernetyczne.

Wykorzystanie matematyki do rozwiązywania złożonych zagadnień praktycznych:

• teoria gier, zagadnienia transportowe, programowanie matematyczne, teoria obsługi masowej, teoria grafów, ...

• modelowanie matematyczne i symulacja komputerowa, modele sztucznego życia.

Istotny element rozwoju teorii organizacji pracy:

• organizacja manufaktur,

• rozwój naukowej organizacji pracy w latach 1890-tych,

• zastosowanie metod badań operacyjnych w przemyśle i powstanie logistyki,

• podejście systemowe w ekonomii,

• metoda analizy przypadków (ang: case studies).

• 3000 p.n.e. - zarządzanie przez Egipcjan gigantycznymi przedsięwzięciami budowy piramid.

• 3000 - 2500 p.n.e. - wykorzystanie przez Sumerów w zarządzaniu spisanych reguł i przepisów.

• 1500 p.n.e. - rozbudowana struktura organizacyjna w Chinach, służąca do kierowania agendami rządowymi.

• 814r p.n.e. - założenie Kartaginy na planie półkola otwartego na morze.

Według legendy opisanej przez Wergiliusza w I księdze "Eneidy" fenicka królowa Dydona osiedlając się na wybrzeżu afrykańskim miała otrzymać od tubylców tyle ziemi na założenie miasta, ile da się przykryć skórą wołu. Królowa ograniczyła teren wyciętym ze skóry cienkim rzemieniem. Koło jest figurą geometryczną o największej powierzchni przy zadanym obwodzie, stąd wydarzenie to można interpretować jako wykorzystanie matematyki dla osiągnięcia maksymalnego efektu przy zadanych ograniczeniach.

• Aleksander Macedoński (356-323 r.p.n.e.) - znakomity strateg i taktyk, uznawany za największego wodza starożytności, szeroko wykorzystywał sztab do planowania kampanii wojennych przeciw Persji.

Na przykład w 334 p.n.e. przed atakiem na Babilon wykonał strategiczny manewr zniszczenia portów w zachodniej części Azji Mniejszej. We wszystkich bitwach stracił mniej niż 1 000 żołnierzy, zabijając setki tysięcy i podbijając znaczącą część ówcześnie znanego świata. Jednym z jego doradców wojskowych był Arystoteles.

• ~214 p.n.e. - zaangażowanie Archimedesa (~287-~212 p.n.e.) z Syrakuz na Sycylii w obronę swego miasta przed Rzymianami.

Przez współczesnych był ceniony głównie jako wynalazca - konstruktor wielokrążków do ściągania galer, olbrzymich dźwigów do przewracania ich do góry dnem, katapult oraz zwierciadła parabolicznego do wzniecania na okrętach przeciwnika pożarów skupianym światłem Słońca. Ten ostatni wynalazek miał według legendy spalić okręt dowódcy Rzymian - Marcusa Claudiusa Marcellusa.

Przypisuje się mu także wyznaczenie zawartości złota w koronie władcy Syrakuz Hierona II. Na podstawie pomiaru ciężaru i objętości wyznaczył gęstość materiału korony, znając ciężary właściwe wchodzących w grę metali ustalił skład użytego stopu.

• Niccolo Fontana (zwany Tartaglia) z Briestu (ok. 1499-1557) w książce Nuova Scienza (Wenecja 1537) opisał trajektorię kuli, w Quesiti et Inventioni Diverse (Wenecja 1543) zagadnienia ruchu pocisku i sztukę fortyfikacji.

Pierwszy podał też rozwiązanie równania algebraicznego trzeciego stopnia: x3 + bx2 + cx + d = 0.

Według ówcześnie obowiązującej dynamiki Arystotelesa kula armatnia miała poruszać się po prostej aż do wyczerpania swego `impetu', a następnie opadać pionowo. Niccolo Fontana jako pierwszy prawidłowo opisał jej trajektorię.

• 1776 rok - Gaspard Monge (1746 -1818), profesor najstarszej francuskiej szkoły inżynierskiej w Mézières, przedstawia królewskiej akademii nauk rozprawę na temat minimalizacji kosztów przemieszczania ziemi z wykopów na nasypy w trakcie budowy dróg. W pracy przedstawił rozwiązanie, nazwane później zagadnieniem transportowym.

Gaspard Monge wraz z Fourierem uczestniczył w kampanii włoskiej i wyprawie do Egiptu prowadzonych przez Napoleona.

• Lazare Nicolas Marguérite Carnot (1753-1823) - prekursor badań operacyjnych w znaczeniu nowożytnym, francuski matematyk, polityk, generał i teoretyk wojskowości, autor klasycznego podręcznika fortyfikacji.

Zajmował się zagadnieniami matematycznymi prowadzenia działań militarnych, w 1784 uruchomił pierwsze na świecie biuro obliczeniowe. Jednym z jego osiągnięć było zorganizowanie w 1793 roku 14 armii przeciw pół milionowi żołnierzy koalicji przeciwników Rewolucji Francuskiej (1789-1799).

• Charles Joseph Minard (1869) - analiza strat armii francuskiej podczas kampanii moskiewskiej 1812-1813 (w odniesieniu do temperatury powietrza podczas odwrotu).

• 1824 rok - zmodyfikowanie przez porucznika artylerii Georga Heinricha Rudolfa Johanna von Reisswitza (1795-1827) założeń gier wojennych.

Nowa koncepcja została przyjęta entuzjastycznie - szef sztabu armii pruskiej von Mueffing miał stwierdzić "To wcale nie jest gra, to są ćwiczenia wojenne!".

Po włączeniu Prus do Niemiec w 1871 roku gry wojenne stały się istotnym elementem szkoleń sztabów niemieckich i przygotowywania operacji wojskowych. Później zostały zaadoptowane przez wiele armii państw europejskich, Rosji, USA i Japonii - doświadczenia Niemców o stulecie wyprzedzały jednak wszystkich pozostałych.

• Przykład absurdalnej decyzji - wytyczenie przez cara Mikołaja I (1796-1855) przebiegu linii Petersburg-Moskwa, ukończonej w 1851 roku.

Będąc świadkiem sporów inżynierów na temat przebiegu 650 km trasy wykreślił na mapie linię prostą, nie zwracając uwagi na topograficzne ukształtowanie terenu, wzgórza, rzeki i bagna. Podniosło to piętnastokrotnie koszty budowy - przekroczyły jedną czwartą rocznych dochodów całego imperium.

W okolicy miejscowości Wierebiowka na odcinku 17 km trasa przebiegała po łuku. Był to obrys kciuka, którym car przytrzymał linijkę. Linię na tym odcinku wyprostowano w 2002 roku.

• Lata 1890-te - Frederick Winslow Taylor (1856-1915), amerykański inżynier, ekonomista i wynalazca, przeprowadza słynne analizy wydajności pracy.

Pracował w stalowni Bethlehem Steel Corporation w Pittsburgu w Pensylwanii. Dzięki niezwykłemu uporowi uzupełnił kwalifikacje zawodowe na studiach wieczorowych.

Najsłynniejsza z jego analiz dotyczyła zwiększenia wydajności pracy łopatą. Obalił powszechne przekonanie, że w miarę zwiększania szufli (a tym samym ciężaru przenoszonej zawartości) uzyskuje się wyższą efektywność pracy. W latach 1890-tych przeprowadził badania na 600-osobowej brygadzie robotników, zatrudnionych w stalowni przy przeładunku materiałów sypkich (węgla, koksu, rudy, popiołów, sody). Wykazał, że najlepsze wyniki osiąga się przy nabieraniu na łopatę 21 funtów (9,75 kg) materiału.

• 1908 rok - zastosowanie pionierskich metod matematycznych przy projektowaniu łącznicy telefonicznej przez duńskiego inżyniera Agnera Krarupa Erlanga (1878-1929).

Przeprowadził badania ilości abonentów, którzy w niewielkiej miejscowości starali się zadzwonić na numery zamiejscowe, a musieli czekać na połączenie gdy wszystkie linie były zajęte. Wydarzenie to rozpoczęło rozwój teorii obsługi masowej (teorii kolejek).

• 1912 rok - badania ekonomii ruchów roboczych, prowadzone przez amerykańskiego inżyniera budownictwa Franka Bunkera Gilbretha (1868-1924) oraz jego żonę Lillian Ewelyn Moller Gilbreth (1878-1972), psychologa przemysłowego.

• Lata 1914-1915 - angielski inżynier techniki samochodowej i lotnictwa Frederick William Lanchester (1868-1946) tworzy równania różniczkowe, opisujące wzajemne oddziaływanie na siebie oddziałów wojskowych.

• 1925 rok - publikacja artykułu "Równowaga gospodarki narodowej ZSRR" ekonomisty Wassyla W. Leontiefa (1906-1994), późniejszego doradcy ekonomicznego komunistycznego rządu Chin (Koumintangu), od 1931 roku osiadłego w USA.

Wprowadził pojęcie macierzy przepływów międzygałęziowych, za które to prace otrzymał nagrodę Nobla w 1973 roku. Rozwinięciem jego metody jest programowanie liniowe w obecnej formie.

• Lata 1930-te - stworzenie i wykorzystanie przez Radio Corporation of America modelu systemu w analizie planów sieci stacji telewizyjnych.

Analiza zagadnienia wykazała, że wysokie koszty produkcji programu telewizyjnego nieuchronnie wymuszą rozdzielenie nowego systemu od sieci radiowej. Przewidziano też, że pojawienie się nowego rodzaju usług zwiększy popyt na urządzenia szerokopasmowe do przekazu sygnału telewizyjnego.

• 1938 rok - powstanie określenia `badań operacyjnych' na oznaczenie wykorzystania przedstawicieli nauki do oceny sytuacji wojskowych oraz rozmieszczenia sprzętu.

Szerokie i efektywne zastosowanie w Wielkiej Brytanii i USA badań operacyjnych, wspomagających planowanie złożonych operacji militarnych metodami matematycznymi.

• Prof. Patrick Maynard Stuard Blackett (1897-1974) tworzy w 1938 roku w strukturze brytyjskiej obrony przeciwlotniczej Departament Badań Operacyjnych.

• John Desmond Bernal (1901-1971) i Solly Zuckerman (1904-1993) rozpoczęli zbieranie i statystyczną analizę danych związanych z efektywnością bombardowań. Ankieterzy zbierali od poszkodowanych dane dotyczące odniesionych obrażeń oraz zniszczeń budynków i mienia.

Solly Zuckerman (1904-1993) - plan bombardowań strategicznej wysepki Pantellaria na Morzu Śródziemnym (1943).

• Lotnictwo i bombardowania - wprowadzenie niezwykle efektywnych grupowych nalotów, powodujących `burzę ogniową'

Brytyjskie centrum dowodzenia obroną przeciwlotniczą.

• Optymalizacja wszystkich elementów taktyki walki z u-bootami - podniesienie w ciągu 2 lat zatapialności niemieckich łodzi podwodnych przez brytyjskie samoloty z 2% do 50%.

• Konwoje

• ilość statków w konwoju proporcjonalna do powierzchni koła (~r2)

• ilość okrętów ochrony proporcjonalna do obwodu zgrupowania (~r)

• im liczniejszy konwój - tym mniejsze straty.

• Lotniskowce pomocnicze ochrony konwojów (frachtowce do przewozu zboża z nadbudowanym drewnianym pomostem i 3-4 jednopłatowcami do zwalczania łodzi podwodnych) - wysoka efektywność prymitywnych rozwiązań.

• USA - optymalizacja zagadnienia zwalczania kamikadze

• 1946 rok - utworzenie RAND Corporation (od ang: research and development - badania i rozwój). Organizację tę powołano dla prowadzenia badań i studiów na potrzeby armii oraz rządu USA.

W 1948 roku w ramach organizacji stworzono w Santa Monika w Kalifornii instytut, który powstał z zespołów badań operacyjnych, a prowadził prace badawcze nad rozwojem strategii, taktyki oraz nowymi typami broni i uzbrojenia. Instytucja wkrótce stała się prywatną i niezależną, rozszerzyła też analizy na zagadnienia między innymi badań kosmicznych i badania strategii gospodarczych.

• 1958 rok - pierwsze zastosowanie metody ścieżki krytycznej CPM (ang: critical path method) oraz techniki oceny i analizy projektu PERT (ang: program evaluation and review technique) przy uruchomieniu produkcji rakiet POLARIS przez firmę Management Systems Corporation.

• Lata 1961-1968 - Robert Strange McNamara (1916-), amerykański biznesmen i polityk, z wykształcenia matematyk, zostaje sekretarzem obrony USA.

Wprowadził analizę systemów i badania operacyjne jako podstawę podejmowania wszelkich decyzji związanych z wyposażeniem i uzbrojeniem, ustanawianiem wymogów dla nowych typów broni oraz rozwiązywaniem zagadnień obronności.

Pojęcia podstawowe badań operacyjnych

• Działanie

• Decyzja

• Decydent

• Kryterium decyzyjne

• Strategia

• Zarządzanie

• Walka

• Badania operacyjne / analiza systemowa

• Logistyka

• Teoria zarządzania

• Działanie (ang: course of action) - zmiana, transformacja stanu systemu lub aktywność systemu podporządkowana osiągnięciu celu, dążenie do osiągnięcia konkretnego rezultatu. Skutkiem działania są wywołane przez nie zmiany stanów systemu.

Działanie może być świadome lub nieświadome, konstruktywne lub destrukcyjne. Możliwość przewidzenia skutków działania pozwala wybrać takie alternatywy działań, które spełnią zadane kryteria, np. minimalizują jakiś wskaźnik jakości lub zwiększają skuteczność w sensie prakseologicznym.

W miarę pojawiania się w działaniu coraz większej liczby elementów nowatorskich, niepowtarzalnych - staje się ono coraz bardziej twórczym i w niektórych dziedzinach nazywane bywa twórczością. Poczynając od rzemiosła artystycznego, poprzez projektowanie, komponowanie - działanie coraz bardziej twórcze.

• Decyzja (ang: decision) - nielosowy wybór konkretnego wariantu działania lub podzbioru ich alternatyw, świadome rozstrzygnięcie w sytuacji wyboru między różnymi możliwościami działania. Podjęta decyzja w istotny sposób wpływa na dalsze zachowanie systemu - zmienia lub transformuje jego przyszłe stany. Wyboru wariantu dokonuje się na podstawie kryterium decyzyjnego wśród znanych i możliwych do osiągnięcia celów lub sposobów działania.

Przykład alternatywnych sposobów podzielenia pomarańczy - na ćwiartki, cząstki równolegle do osi lub prostopadle (plasterki). Wybór najwłaściwszego zależy od postawionego przed działaniem celu.

Przykład: decyzje związane z kierowaniem statkiem polegają na dokonywaniu wyborów spośród repertuaru możliwych położeń steru (kąta jego wychylenia i momentu zmiany kursu) oraz następujących stanów silnika - cała naprzód, powoli naprzód, maszyny stop, powoli wstecz, cała wstecz.

Przedmiot wyboru -

• obiekt materialny (przedmiot, urządzenie techniczne, instytucja, osoba, grupa społeczna),

• cel działania (np. wybór obiektu ataku spomiędzy alternatywnych celów, zdobycie przez atakujące oddziały wzgórza czy przełęczy, wyprodukowanie produktu A czy produktu B, opanowanie rynku produkcji mikroprocesorów czy gier wideo, wybór kierunków inwestowania, technologii),

• miejsce w przestrzeni (np. wybór miejsca skoncentrowania oddziałów, lokalizacji inwestycji),

• czas (np. określenie najodpowiedniejszej chwili rozpoczęcia operacji wojskowej, kampanii reklamowej, zmiany kursu statku),

• sposób działania (np. wybór strategii wdrażania innowacji, sposobu transportu towaru drogą morską czy koleją, zakupu licencji lub opracowania własnego rozwiązania technicznego),

• podział zasobów (np. podział obwodów wyborczych w sposób zapewniający danej partii uzyskanie największej liczby mandatów, optymalny podział zasobów na wykonanie różnych prac),

• relacje między elementami (np. pokonanie konkurenta, rozpoczęcie współpracy lub połączenie się z nim),

• przekształcenie struktur organizacyjnych.

Pojęcia podstawowe

• Decydent (ang: decision maker) - osoba lub instytucja podejmująca decyzję.

• Kryterium decyzyjne (ang: criterion) - zdefiniowany przez decydenta wskaźnik, pozwalający ocenić rozważane warianty pod względem spełniania określonych celów.

• Strategia (ang: strategy) - zasada nakazująca w sytuacji podejmowania decyzji podjęcie określonego działania ze zbioru dostępnych działań alternatywnych, przyporządkowująca wystąpieniu konkretnej sytuacji podjęcie określonych działań. Wybór strategii zależy od zasobu informacji posiadanych w chwili podejmowania decyzji. Np. strategia marketingu - sposób prowadzenia działań na rynku, mający na celu zachęcenie do nabywania towaru.

Określenie `strategia' pierwotnie było związane ze sztuką dowodzenia.

• Zarządzanie (ang: management) - działalność kierownicza polegająca na wyznaczaniu celów oraz powodowaniu [doprowadzaniu do] ich realizacji w jednostkach organizacyjnych podległych zarządzającemu. Podstawą podejmowanych w trakcie zarządzania decyzji mogą być badania operacyjne lub analiza systemów.

Dowodzenie - w przypadku jednostek wojskowych.

• Walka (ang: conflict) - świadome działania co najmniej dwóch różnych podmiotów, dążących do niezgodnych ze sobą celów, usiłujących przeszkadzać sobie nawzajem w realizacji swoich celów. Pojęcie walki uogólnia wszelkie przypadki działań przeszkadzających (utrudniających) innym w ich dążeniach, jest też uniezależnione od specyficznych cech walki zbrojnej jako takiej. Obejmuje nie tylko przypadki działań militarnych ale także rywalizację gatunków, wszelkiego rodzaju współzawodnictwo, konkurencję handlową, debaty parlamentarne, spory prawne, dyskusje, starania o rękę lub względy wybranki, grę w szachy, zawody sportowe. Działania walki mogą obejmować fizyczne zniszczenie drugiej jednostki, fizyczne lub psychiczne obezwładnienie, podporządkowanie sobie, pozbawienie narzędzi działania, dostępu do określonych miejsc w przestrzeni lub zasobów (między innymi informacji), możliwości wykonywania skutecznych działań przez stronę przeciwną.

• Badania operacyjne (ang: operational research, am: operations research) - naukowa metodologia analizy operacji (czynności celowych) i obiektywnej oceny decyzji (między innymi stopnia związanego z nią ryzyka), dostarczania decydentom podstaw ilościowych do podjęcia decyzji związanych z zarządzaniem lub projektowaniem systemu technicznego. Jest oparta na wyborze najlepszego rozwiązania na podstawie oceny możliwych skutków alternatywnych działań. Badania operacyjne obejmują opracowywanie metod analizy celowych działań (operacji) oraz obiektywną (przede wszystkim ilościową) ocenę porównawczą rozwiązań.

Celem badań operacyjnych jest przeprowadzenie obiektywnej analizy zjawiska, ilościowa ocena przewidywanych działań, ewentualne znalezienie innych wariantów (alternatyw) rozwiązania, różnych od wcześniej branych pod uwagę [rozważanych], oraz wybór najkorzystniejszego wariantu decyzji.

W badaniach operacyjnych można wyróżnić następujące etapy:

• sformułowanie zagadnienia - obejmuje określenie przedmiotu i celu badań, analizę czynników, współmierności nakładów i wyników, szacowanie wpływu jaki działanie wywrze na inne elementy systemu. Jest to etap o istotnym znaczeniu dla dalszych badań. Złożoność zagadnienia, skomplikowanie wzajemnych relacji oraz ich powiązanie z innymi zagadnieniami wymaga bowiem dokonania uproszczeń, które mogą znacząco wpłynąć na wyniki dalszej analizy. Jednym z rezultatów przeprowadzenia etapu formułowania zagadnienia jest wybór zbioru wskaźników, które w zadowalający sposób charakteryzują zarówno operację jak jej organizację i zarządzanie (sterowanie) nią.

• budowa sformalizowanego (zwykle matematycznego) modelu rozważanego systemu czy też działania (operacji). Wybór odpowiedniego modelu jest niezwykle istotny dla powodzenia projektu. Etap ten obejmuje również analizę potencjalnych metod numerycznego rozwiązania modelu.

• zebranie niezbędnych informacji i danych wejściowych - często wymaga zorganizowania operacji ich zbierania, przetwarzania i gromadzenia. Elementem tego etapu może też być analiza kosztów stworzenia i działania systemu pozyskiwania informacji oraz oszacowanie potencjalnych strat wywołanych przez brak danych.

• analiza modelu i wyznaczenie rozwiązania - wykorzystanie różnych metod i algorytmów optymalizacji, modelowania statystycznego lub teorii gier. Etap ten zwykle wiąże się z przeprowadzeniem obliczeń numerycznych, jednak może być też oparty wyłącznie na ocenach ekspertów (tak zwana metoda delficka). Oceny ekspertów są ilościowymi lub jakościowymi oszacowaniami procesów, zjawisk, prognozowanych alternatyw, ich następstw oraz konsekwencji - nie poddających się bezpośredniemu pomiarowi.

• sprawdzenie adekwatności modelu w stosunku do rozważanego zagadnienia i ilościowa ocena jakości rozwiązania. Konieczność stosowania różnych form abstrakcji upraszczającej oraz homomorfizm modelu powodują, że model tylko częściowo odwzorowuje zagadnienie rzeczywiste. Przydatność modelu oraz jakość otrzymanego wyniku można ocenić porównując jego przewidywania z odpowiadającymi im obserwacjami realnych skutków.

• korekta modelu i/lub jego rozwiązania. Wykorzystuje rezultaty przeprowadzonych na poprzednim etapie działań sprawdzających adekwatność modelu do poprawy jakości modelu oraz zweryfikowania słuszności uprzednio przyjętych hipotez i założeń upraszczających zagadnienie,

• wdrożenie wyników - etap ten bardzo często kończy się również sformułowaniem postulatów dotyczących zmian w sposobie analizy konkretnego zagadnienia lub metodologii badań operacyjnych.

• Badania operacyjne są systemem różnego rodzaju metod matematycznych, narzędzi służących porównaniu możliwych rozwiązań i konsekwencji ich przyjęcia. Obejmują takie zagadnienia matematyczne jak rachunek prawdopodobieństwa, statystyka, teoria grafów, analiza sieci, programowanie liniowe i dynamiczne, teoria i metody optymalizacji, procesy Markowa (sekwencje stanów lub zdarzeń, w których wielkość wyjściowa zależy tylko od ostatniego stanu, a nie zależy od stanów poprzedzających), sytuacje konfliktowe i teoria gier, teoria obsługi masowej, zarządzanie zapasami.

• Analiza systemowa, analiza systemów (ang: systems analysis) - metodologia badania dowolnych obiektów traktowanych jako systemy, pod kątem przygotowania podstaw do podjęcia decyzji. W szczególności dotyczy systemów związanych z projektowaniem technicznym oraz działalnością gospodarczą, społeczną i ekologiczną.

Termin 'analiza systemowa' został stworzony pod koniec lat 1940-tych przez analityków z RAND Corporation. Rozwój metod analizy systemów był związany z udziałem Stanów Zjednoczonych w II wojnie światowej - planowaniem i wyborem systemów uzbrojenia, analizami rozwiązań logistycznych. Z tego względu analiza systemów była w USA odpowiednikiem badań operacyjnych stosowanych w Wielkiej Brytanii. W późniejszym czasie była wykorzystana między innymi do optymalizacji systemu obrony przeciwrakietowej oraz środków przenoszenia broni jądrowej.

Ciąg działań analizy systemów:

• zdefiniowanie celów, które mają być zrealizowane (osiągnięte) przez system - identyfikację zagadnienia

• badanie wszelkich możliwych alternatywnych sposobów osiągnięcia tych celów oraz zaprojektowanie alternatywnych systemów, które zapewnią ich osiągnięcie,

• ocenę przyszłych pozytywnych i negatywnych skutków każdego z alternatywnych wariantów rozwiązania zagadnienia, wzajemne porównania rozwiązań w kategoriach efektywności i kosztów,

• wybór najlepszego rozwiązania przez porównanie ocen każdego z wariantów, pod różnym kątem i według różnych kryteriów.

• krytyczne analizy celów i innych założeń przyjętych w czasie badań,

• odkrywanie nowych alternatyw,

• wyznaczanie nowych celów, oraz ewentualne rozpoczęcie cyklu działań od początku. [ itd.].

• Logistyka (ang: logistics) - nauka zajmująca się organizacją zintegrowanych systemów planowania, koordynowania, sterowania i kontrolowania obiegu dóbr materialnych oraz informacji związanych z nimi i z uwarunkowaniami tego procesu, a także optymalizacją tak zdefiniowanych działań i celów. W szczególności zajmuje się rozmieszczeniem, stanem i przepływem elementów, które są przedmiotem tych procesów - ludzi, dóbr materialnych, informacji, środków finansowych, transportem chorych i rannych.

Termin `logistyka' pochodzi od francuskiego określenia `maître du logie'. W czasie drugiej wojny światowej określenie to zostało rozpowszechnione przez Amerykanów. W Stanach Zjednoczonych oznaczało zagadnienia związane z techniką pakowania zapasów oraz sposobem prowadzenia obliczeń niezbędnych ilości poszczególnych dóbr. Jak w szczególności wykazały działania militarne na Pacyfiku sposób organizacji dostaw w warunkach wojny często jest ważniejszy od usprawniania wyposażenia i broni.

• Teoria zarządzania - (ang: scientific management). Wraz z rozwojem stosowanych metod rozszerzał się zakres zagadnień, które były przedmiotem szeroko rozumianych badań operacyjnych i techniki systemów. Coraz częściej spotyka się łączne określenia typu - badania operacyjne i technika systemów (ang: operational research and system analysis/technique) przede wszystkim w projektowaniu technicznym, czy też - badania operacyjne i teoria zarządzania (ang: operational research and management science, w skrócie OR/MS) w ekonomii. Używane też bywają określenia 'inżynieria przemysłowa' (ang: industrial engineering) lub nauka/teoria podejmowania decyzji (ang: decision science). Istnienie tak wielu terminów spowodowało jednak odrodzenie się określenia 'badania operacyjne', obejmującego zagadnienia wszystkich wymienionych kierunków pobocznych.

Można zauważyć wyraźną tendencję do stopniowego zrastania się inżynierii systemów, techniki systemów, badań operacyjnych i logistyki w coraz bardziej ujednoliconą systemową naukę stosowaną.

Metody badań operacyjnych

• Metody sieciowe - metody oparte na teorii grafów; metoda CPM ścieżki krytycznej, metoda PERT.

• Programowanie liniowe (ang: linear programming) - wykorzystanie metod liniowego zagadnienia optymalizacji.

• Teoria obsługi masowej, teoria kolejek (ang: theory of queues, queueing theory) - bada prawidłowości statystyczne w operacjach składających się z dużej liczby jednorodnych operacji elementarnych. W zagadnieniach tych strumień zgłoszeń na wykonanie operacji elementarnych nadchodzi w losowych (przypadkowych) momentach czasu lub jest obsługiwany w odcinkach czasu o losowej długości. Istotnym czynnikiem, który nie daje się zaniedbać, jest tworzenie się kolejek do obsługi. Przy dużej liczbie kanałów w systemie powstają straty spowodowane ich niewykorzystaniem i przestojami, zaś przy małej liczbie - straty wywołane tworzeniem kolejek i czekaniem na obsługę. Oceniana jest jakość i zdolności przepustowe systemu obsługi przy różnych zasadach tworzenia kolejek.

• Teoria odnowy (ang: renewal theory) - jej przedmiotem jest badanie operacji związanych ze zmianą stanu urządzeń, oceną ich jakości, efektywnymi planami remontów i wymiany, nakładami związanymi z wymienionymi czynnościami, a przede wszystkim wybór optymalnej strategii działania.

• Teoria gier (ang: game theory) - metodologia rozwiązywania zagadnień konfliktowych] umożliwia analizę zagadnień podejmowania decyzji w sytuacjach konfliktowych lub w warunkach nieokreśloności.

Teoria modelowania

• Wyjściowa definicja modelu:

Model to abstrakcyjny lub materialny system, który odzwierciedlając lub odtwarzając przedmiot badania - zdolny jest zastępować go w taki sposób, że badanie modelu dostarcza nam nowej informacji o przedmiocie analizy.

• Formalna definicja modelu opiera się na leżących u podstaw modelowania pojęciach izomorfizmu i homomorfizmu.

Jest to izomorfizm i homomorfizm zbiorów (lub obiektów matematycznych typu dziedzin, systemów relacyjnych) ze względu na relacje.

Izomorfizm

• Dwa zbiory D1 i D2 są izomorficzne ze względu na relacje (stosunki, zależności) R1 i R2 określone odpowiednio na D1 i D2, jeśli są spełnione następujące warunki:

• istnieje taka odwzorowująca funkcja (proces, algorytm, odpowiedniość, operator) F, na mocy której każdy element zbioru D1 odpowiada jednemu i tylko jednemu elementowi zbioru D2

• odwzorowanie odwrotne F-1 ma tę własność, że każdy element w zbiorze D2 jest przyporządkowany jednemu i tylko jednemu elementowi w D1

• zawsze gdy elementy zbioru D1 pozostają w stosunku R1, ich F-obrazy znajdują się w stosunku R2 i na odwrót.

Homomorfizm

• Dwa zbiory D1 i D2 są homomorficzne ze względu na relacje (stosunki, zależności) R1 i R2 określone odpowiednio na D1 i D2, jeśli są spełnione następujące warunki:

• istnieje taka odwzorowująca funkcja (proces, algorytm, odpowiedniość, operator) F, na mocy której każdy element zbioru D1 odpowiada jednemu i tylko jednemu elementowi zbioru D2

• zawsze gdy elementy zbioru D1 pozostają w stosunku R1, ich F-obrazy znajdują się w stosunku R2.

• Izomorfizm (od greckiego isos - jednakowy i morphé - forma) jest relacją tożsamości strukturalnej i/lub funkcjonalnej systemów. Jest relacją zwrotną, symetryczną i przechodnią. Pojęcie to powstało na gruncie matematyki abstrakcyjnej i jedynie w niej może być stosowane w całkowicie ścisły sposób.

W ogólnym rozumieniu izomorfizm obejmuje przekształcenia obiektów matematycznych typu dziedzin, systemów relacyjnych - w wyniku których to przekształceń utrzymywane zostają ich wszystkie (a w każdym razie przynajmniej - wszystkie istotne) właściwości.

Przykłady: izomorfizm między negatywem a odbitką zdjęcia fotograficznego, między odbitkami z jednego negatywu, między dźwiękiem zapisanym na taśmie magnetycznej a płycie analogowej. Izomorfizm trójkątów ma miejsce gdy ich kąty są równe, natomiast długość boków może być dowolna. Można też mówić o ogólnym izomorfizmie obrazów konkretnego obiektu lub zjawiska, formułowanych w języku fizyki i matematyki, ekonomii.

• Homomorfizm (od greckiego homoios - podobny i morphé - forma) jest relacją podobieństwa strukturalnego lub funkcjonalnego. Jest uogólnieniem izomorfizmu, osiąganym przez rezygnację z wymogu wzajemnej jednoznaczności elementów i relacji w obu zbiorach, na rzecz jednoznacznej odpowiedniości tylko w jednym kierunku. Dopuszcza uproszczenie jednego układu względem drugiego. Wymaga zwrotności i przechodniości relacji, ale nie jej symetryczności.

Przykłady: miejscowość i jej mapa, program komputerowy i jego schemat blokowy. Przyporządkowanie poszczególnym ludziom z jakiejś zbiorowości ich wieku jest homomorficznym odwzorowaniem relacji starszeństwa zachodzącej w tej grupie. Jednak homomorficzna mapa nie pozwala odtworzyć innych relacji w grupie, chociażby ich wzrostu, płci, itp. Homomorfizm między fragmentem terenu a mapą powoduje, że tylko niektóre aspekty zostają uwzględnione na mapie: rzeźba terenu, pokrycie roślinnością. Relacja homomorfizmu między konkretnym człowiekiem a informacjami o nim w bazie danych.

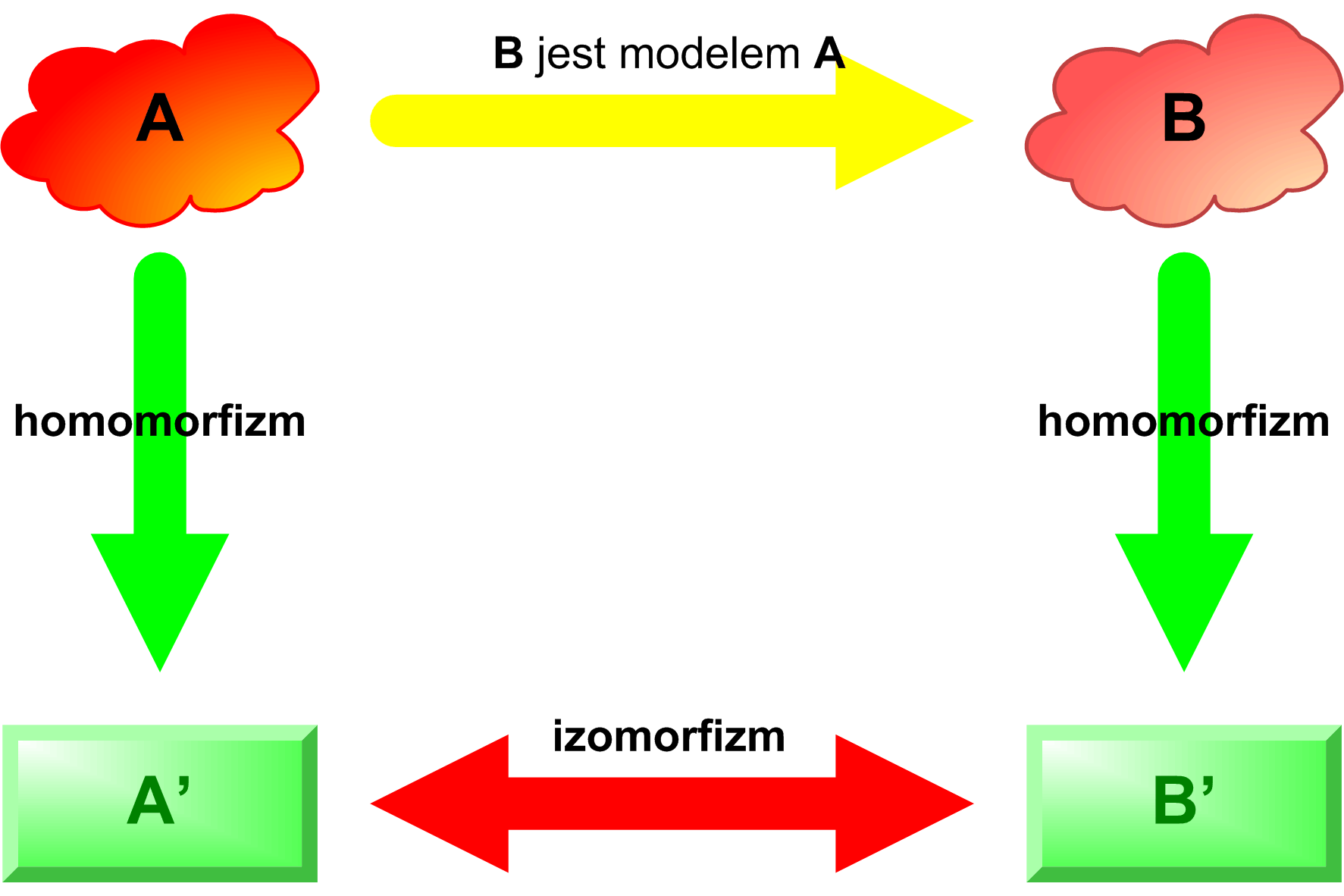
Model

• Przedmiot (system elementów) B jest modelem przedmiotu A wtedy i tylko wtedy, gdy istnieje taki homomorficzny obraz A' przedmiotu A, i taki homomorficzny obraz B' przedmiotu B, że A' i B' mają względem siebie charakter izomorficzny.

Klasyfikacja modeli

• Modele materialne (rzeczywiste, substancjalne, konkretne, fizyczne) - są realnie istniejącymi obiektami, zdarzeniami, sytuacjami.

• Modele podobne geometrycznie - konstrukcje budowane by odtworzyć lub odzwierciedlić cechy lub stosunki przestrzenne przedmiotu. Cechą charakterystyczną jest podobieństwo geometryczne, choć dodatkowo mogą być odzwierciedlane takie cechy jak kolor, faktura powierzchni itp. Przykłady: kopie rzeźb, obrazów, makiety, plany, sobowtóry znanych postaci.

• Modele homologiczne - odtwarzają dynamikę badanych procesów, różnego rodzaju zależności i prawidłowości związków, struktury. Ich podstawą jest fizyczne podobieństwo modelu i przedmiotu oryginalnego, identyczność lub podobieństwo ich fizycznej natury. Często następuje zmiana skali przestrzennej lub czasowej. Przykłady: techniczne instalacje pilotowe, modele do badań aero- i hydrodynamicznych, zwierzęta doświadczalne (w wielu przypadkach mysz doświadczalna jest wystarczająco dobrym modelem człowieka).

• Modele analogowe - układy o innej naturze fizycznej, niepodobne pod względem fizycznym ani geometrycznym. Za pomocą identycznego formalizmu opisywane jest zachowanie układów o różnej naturze fizycznej. Szczególnie intensywny rozwój i zastosowanie analogowych maszyn liczących nastąpił w drugiej połowie lat 1930-tych. Przyczyniło się do tego uruchomienie produkcji wysokiej jakości elementów elektro- i radiotechnicznych.

• Modele abstrakcyjne - nawet gdy ich elementy i relacje są utrwalone przy pomocy środków materialnych - wszelkie przekształcenia i transformacje są dokonywane na płaszczyźnie świadomości, przy zastosowaniu określonych reguł semantycznych, zasad i praw logicznych, matematycznych, fizycznych itp.

• Modele myślowe - stworzone w mózgu modele działania systemu, pozwalające przewidywać jego zachowanie. Eksperymenty myślowe ludzi w znacznej mierze zastępują metodę prób i błędów stosowaną przez zwierzęta.

• Modele werbalne - przedstawione w sposób opisowy, przy wykorzystaniu środków werbalnych (np: hasła encyklopedii, opisy, książki). Modele takie mimo stosunkowo nieprecyzyjnego i niesformalizowanego charakteru odgrywają w niektórych dziedzinach ogromną rolę (np. psychoanalizie, socjologii).

• Modele ikoniczne (obrazowe) - zachowują w pewien sposób geometryczne podobieństwo do badanego przedmiotu. Bardzo często stanowią dwuwymiarowe odwzorowanie trójwymiarowych obiektów lub ich struktury. Przykłady: zdjęcia, schematy, diagramy, organigramy, grafy, animacje procesów.

• Modele symboliczne (formalne) - w których elementy, relacje i własności modelowanych zjawisk są wyrażone za pomocą określonych znaków. Cechą szczególną jest brak podobieństwa między elementami modelu a przedmiotem. (np. wzory strukturalne w chemii, wzory matematyczne).

• Modele logiczne - wykorzystują logikę formalną. W odróżnieniu od matematycznych odznaczają się mniejszą złożonością opisu modelu, odtwarzają jedynie pewną organizację, strukturę czy relacje

Modele matematyczne

• Ze względu na rolę matematyki jako źródła ścisłego języka formalnego nauki, jednymi z najistotniejszych dziedzin jest tworzenie modeli matematycznych.

Modelami matematycznymi nazywa się modele będące interpretacjami aksjomatycznych teorii dedukcyjnych, wyrażone w formalnym języku symbolicznym matematyki.

Abstrahowanie

• Abstrahowanie jest operacją odtwarzania i odzwierciedlania przez model przedmiotu badań w uproszczonej i schematycznej postaci.

Rodzaje abstrakcji

• Abstrakcja utożsamienia - pomijanie własności i cech niepodobnych u porównywanych przedmiotów a wyróżnienie jednakowych (abstrakcja uogólniająca). Przykłady: wzory chemiczne abstrahują od własności, cech i stanów skupienia substancji; modele społeczne abstrahują od ustroju politycznego państw oraz różnic historycznych, narodowych i geograficznych.

• Abstrakcja izolująca (analityczna) - abstrahowanie od pewnych własności przedmiotów (np. koloru), któremu czasami towarzyszy formalna abstrakcja uprzedmiotowienia. Uprzedmiotowieniem było np wprowadzenie w XVIII w. pojęcia 'cieplika' jako nieważkiej i niezniszczalnej substancji przemieszczającej się z ciał ciepłych do zimnych, pewnej analogii cieczy termodynamicznej. W rzeczywistości ani cieplik ani eter (nieważki i sprężysty fluid - nośnik fal elektromagnetycznych) nie istnieją.

• Abstrakcja myślowego wyróżnienia części i abstrahowania od całości - np. modele organów wewnętrznych ciała, cząstkowe modele procesów wchodzących w skład bardziej złożonej całości, wycinkowe zadania ekonomiczne w ramach większych przedsięwzięć.

• Abstrakcja nieuwzględniania zmiany i rozwoju przedmiotu, zmienności, nieokreśloności, niestałości jego granic, płynności, dialektyczności (abstrakcja konstruktywizacji) - prowadzi do powstania sztywnych i statycznych przedmiotów, odtworzenia własności niezmiennych w czasie, cech stałości, niezmienności (np. modele atomów, molekuł chemicznych, systemów społecznych). Przykłady: przedsiębiorstwa niezależne od zmian zatrudnienia, pojęcie Państwa Polskiego na przestrzeni tysiącleci, niezależnie od geograficznych zmian granic, chwilami formalnego braku państwowości.

• Abstrakcja uproszczenia - abstrahowanie od nadmiernego skomplikowania przedmiotu, różnorodności wewnętrznych związków i relacji nieistotnych lub przypadkowych, zewnętrznych wpływów i oddziaływań, a zachowanie jedynie podstawowych, najistotniejszych. Przykład: modelowanie systemu planetarnego wymaga pominięcia znakomitej większości obiektów kosmicznych, ograniczenia zainteresowania do najwyżej kilkunastu, zastąpienia każdego obiektu punktem o masie planety, uwzględniania jedynie relacji między każdą z planet z osobna a Słońcem, zaniedbania wzajemnych oddziaływań pozostałych obiektów między sobą.

• Abstrakcja idealizacji - abstrahowanie nie od jakichś własności lub uproszczenie przedmiotu, ale wyolbrzymienie, absolutyzacja i doprowadzenie do granicznych postaci pewnych obserwowalnych stanów lub własności. W wyniku powstają idealizacje nie mogące istnieć realnie, ale posiadające nieidealne odpowiedniki w świecie rzeczywistym. Przykłady: założenie ciągłości materii, pojęcie gazu idealnego, cieczy nieściśliwej, absolutnie twardego ciała (nawet diament nie posiada tej właściwości), układu przekazującego informację bez pomyłek, homo oeconomicus (człowieka, który kieruje się wyłącznie własnym interesem i chęcią zysku), kapitalizmu i komunizmu jako abstrakcyjnych pojęć nie występujących nigdzie na świecie w czystej postaci, tworów matematycznych w rodzaju punktu, prostej, okręgu.

• Abstrakcja potencjalnej realizacji - abstrahowanie od realnych (w wypadku systemów społecznych między innymi historycznych) granic możliwości wykonawczych, konstrukcyjnych oraz uwarunkowań ograniczoności życia w czasie i przestrzeni. (np: nieskończenie długa taśma z danymi w hipotetycznej maszynie Turinga, dowolnie bogate alfabety systemów semiotycznych)

• Strukturalizacja - abstrakcja wyróżnienia pewnej 'czystej' struktury, jednakowej w rozmaitych systemach, abstrahując od natury lub własności elementów. Np. klasyfikacja typów systemów, traktująca kurę znoszącą jajko i fabrykę produkującą traktor jako systemy otwarte (pobierające substancje fizyczne i energię z otoczenia, emitujące odpady) oraz scentralizowane (ze względu na wyróżnioną rolę mózgu ptaka i dyrekcji zakładów w sterowaniu obiektem).

Modele funkcjonalne a strukturalne

Stosowanie różnych podejść przy wyznaczaniu zależności w badanym obiekcie powoduje wyodrębnienie dwóch skrajnie różniących się, z poznawczego i praktycznego punktu widzenia, typów modeli:

• Modele funkcjonalne - zachowujące się jak obiekt modelowany, ale posiadające zupełnie inną strukturę wewnętrzną. Są to empirycznie dobrane zależności imitujące zachowanie się modelowanego układu, widzianego z zewnątrz. Model imituje zewnętrzne zależności systemu z otoczeniem. Wobec niewykorzystywania jakichkolwiek informacji o mechanizmie procesów zachodzących w układzie, model stanowi "czarną skrzynkę". Tego typu podejście było podstawą sterowania układami technicznymi. Zależności opisujące sterowany obiekt są identyczne w przypadku linii produkcyjnej landrynek i reaktora jądrowego. Modele te nie zawierają jakiejkolwiek informacji poza oryginalnymi danymi zależności statystycznych.

• Modele strukturalne - których struktura wewnętrzna odpowiada strukturze obiektu. Modele te odwzorowują wewnętrzną organizację oryginału. Oparte są na matematycznej analizie praw rządzących odpowiednimi dziedzinami. Ten typ jest charakterystyczny dla nauk ścisłych, w których teoria ma strukturę dedukcyjną i przyjmuje postać systemów aksjomatycznych. Modele strukturalne powstają przez agregację opisów poszczególnych procesów elementarnych, wyróżnionych w obiekcie podczas teoretycznej analizy jego działania, przy uwzględnieniu relacji między podukładami. Ten typ modeli jest szczególnie przydatny w badaniach modelowych (symulacji), pozwala na przenoszenie wyników uzyskanych w trakcie analizy modelu na oryginał.

---