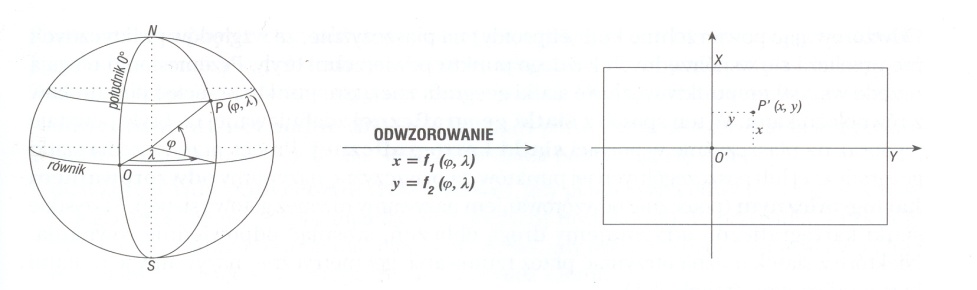
Odwzorowaniem jednej powierzchni na drugą nazywamy każda wzajemnie jednoznaczną odpowiedniość punktową miedzy powierzchnią nazywana oryginałem a powierzchnia nazywana obrazem

Odwzorowanie kartograficzne jest umownym, określonym matematycznie sposobem przyporządkowania punktom powierzchni elipsoidy, kuli punktów na płaszczyźnie

W kartografii powierzchnia oryginału i powierzchnia obrazu są powierzchniami regularnymi. W odwzorowaniach regularnych:

- obrazem punktu jest punkt,

- obrazem krzywej jest krzywa,

- obrazem kata jest kat,

- obrazem powierzchni jest powierzchnia.

FUNKCJE ODWZOROWAWCZE MAJA POSTAĆ

x = x (B, L) parametrem są współrzędne prostokątne

y = y (B, L)

ၧ = ၧ (B, L) parametrem są współrzędne biegunowe

ၤ = ၤ (B, L)

Pojęcie skal i zniekształceń odwzorowawczych

1. Odwzorowanie powierzchni elipsoidy na płaszczyznę.

2. Zmniejszenie wszystkich elementów liniowych obrazu płaskiego w stałym stosunku 1 :M.

Liczbę m₀ = 1 :M nazywamy skalą główna mapy

Niech ds.' oznacza długość nieskończenie małego łuku na powierzchni oryginału, a ds długość odpowiadającego mu łuku na obrazie m = ds' / ds

nazywamy elementarną skalą długości (skalą liniową), lub skalą długości.

Jest to Stosunek różniczkowego przyrostu długości na płaszczyźnie odwzorowawczej do odpowiadającego przyrostu długości łuku na elipsoidzie (lub na umownej powierzchni odniesienia)

Elementarna skala długości w danym odwzorowaniu zależy od współrzędnych B i L określających położenie punktu, i od azymutu A elementu liniowego ds.

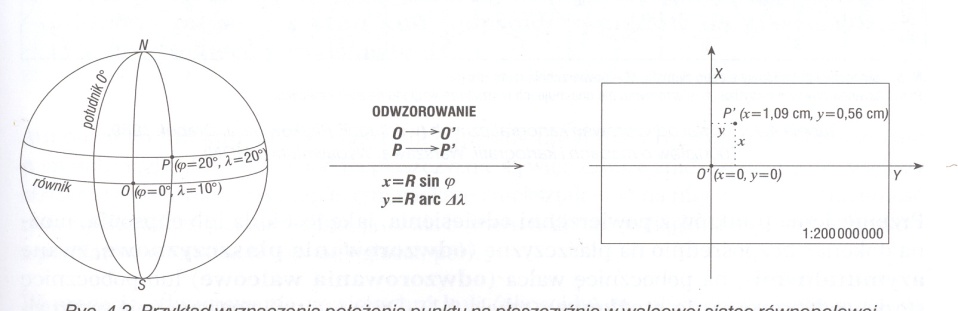
m = m (B, L, A)

Przykład wyznaczenia położenia punktu na płaszczyźnie w odwzorowaniu walcowym równopolowym

WYBÓR ODWZOROWANIA

Wybór odwzorowania dla map uwzględnia przede wszystkim kryterium występujących na mapie zniekształceń odwzorowawczych.

Według tego kryterium można wyróżnić odwzorowania:

• wiernokątne, m_B = m_L gdzie m_B=m_x a m_L=m_y

• wiernopolowe, m_B • m_L = 1

• wiernoodległościowe, m_B = 1, lub m_L = 1

• „dowolne”.

WŁAŚCIWOŚCI MAP

• zachowują zgodność oryginalnych i obrazowych kierunków, a więc kształtów i orientacji elementów i całego układu,

• zachowują stałość stopnia zmniejszenia wszystkich wyróżnionych na mapie pól powierzchni, a więc i ich właściwe relacje wzajemne,

• zachowują stałość stopnia pomniejszenia długości elementów zorientowanych

UKŁADY KARTOGRAFICZNE W POLSCE PSWG'92

PSWG'92 został wprowadzony do stosowania w Polsce Rozporządzeniem Rady Ministrów z dnia 8 sierpnia 2000 r. (DZ.U. nr 70 z dn. 24.08.2000 r. , poz. 821)

Rozporządzenie z dnia 8 sierpnia 2000 wprowadziło do stosowania nowy Państwowy System Współrzędnych Geodezyjnych oparty o Europejski System Odniesień Przestrzennych ETRF'89.
W oparciu o nowy system przestrzenny zdefiniowano nowe kartograficzne układy współrzędnych powstałe poprzez aplikacje odwzorowania Gaussa-Krugera elipsoidy GRS'80 (WGS'84).
Nowe układy otrzymały nazwy:

1992 (układ jednostrefowy)

2000 (układ czterostrefowy)

Obecnie w polsce obowiazują układy współrzędnych; „2000”, „1992”, „1965”, „1942”, GUGIK-80, UTM i układy lokalne

Twierdzenia Tissota - twierdzenia teroii zniekształceń odwzorowawczych sformułowane przez francuskiego kartografa Nicolas Auguste Tissot'a.

Twierdzenie I (dot. siatek ortogonalnych) - w dowolnym odwzorowaniu jednej powierzchni na drugą istnieje zawsze przynajmniej jedna (jeśli jest to powierzchnia regularna) albo tylko jedna (jeśli jest to powierzchnia nieregularna) siatka ortogonalna (kiedy południki z równoleżnikami tworzą kąty proste) na powierzchni oryginału (kuli zmiemskiej), której obraz na powierzchni drugiej (mapie) jest również siatką ortogonalną.

Twierdzenie II (dot. elipsy zniekształceń) - w regularnym odwzorowaniu jednej powierzchni na drugą zniekształcenia odwzorowawcze długości we wszystkich kierunkach wychodzących z danego punktu można przedstawić w postaci elipsy, której półosie odzwierciedlają maksymalne zniekształcenia w kierunkach głównych (tzn. w kierunku południków i równoleżników).

Skala długości:
ds' - elementarny odcinek na elipsoidzie a ds. - odcinek na mapie

Skala pól:

Skala zniekształceń pól: Z_f = f-1

Skala zniekształceń długości: Z_m = m-1

ODDWZOROWANIA KARTOGRRAFICZNE

• siatka geograficzna - układ południków i równoleżników wyznaczony na kuli ziemskiej lub na globusie.

• siatka kartograficzna - układ południków i równoleżników na płaszczyźnie

Odwzorowanie kartograficzne - sposób przeniesienia siatki geograficznej na płaszczyznę.

TYPY ODWZOROWAŃ ZE WZGLĘDU NA ZNIEKSZTAŁCENIA

Rozwinięcie powierzchni kuli na płaszczyźnie jest niemożliwe bez jej zniekształcenia. Oznacza to, że wszystkie odwzorowania kartograficzne zniekształcają rzeczywisty obraz Ziemi. Zniekształcenia mogą dotyczyć: powierzchni, kątów, odległości. Są odwzorowania, które zachowują jedną cechę, np.

• Odwzorowania wiernopowierzchniowe (wiernopolowe) - wierne powierzchnie (najczęściej stosowane w atlasach powszechnego użytku, wykorzystuje się je do obliczania powierzchni określonego zjawiska geograficznego, np. powierzchni lasów, łąk, powierzchni jednostek administracyjnych itp.),

• Odwzorowania wiernoodległościowe - równe odległości (stosowane np. w komunikacji radiowej),

• Odwzorowania wiernokątne - wierne kąty (stosowane np. w komunikacji morskiej i lotniczej, na mapach topograficznych, na analitycznych mapach meteorologicznych itp.).

Zniekształcenia spowodowane odwzorowaniem są najmniejsze w pobliżu miejsca (punktu lub linii) styczności. W zamieszczonych obok odwzorowaniach jest to równik. Im dalej od niego, tym okręgi są bardziej zniekształcone, a zmiany kształtu i wielkości okręgów odpowiadają zmianom powierzchni, odległości i kierunków.

TYPY ODWZOROWAŃ ZE WZGLĘDU NA POŁOŻENIE PŁASZCZYZNY LUB POWIERZCHNI POMOCNICZEJ WZGLĘDEM POWIERZCHNI KULI

W celu zminimalizowania nieuchronnych odkształceń siatki kartograficznej w stosunku do oryginału, powierzchnie odwzorowania układa się na różne sposoby względem geometrycznej powierzchni Ziemi:

• umieszcza nad Ziemią, styka z nią lub przecina nimi jej powierzchnię; w ten sposób możemy wyróżnić:

• odwzorowania styczne,

• odwzorowania sieczne,

• odwzorowania bez punktu wspólnego.

Typy odwzorowań ze względu na rodzaj powierzchni rzutowania

Najprostszymi odwzorowaniami kartograficznymi są RZUTY. W zależności od rodzaju powierzchni, na którą rzutujemy, odwzorowania te dzielimy na:

Odwzorowania kartograficzne klasyczne:

• płaszczyznowe (azymutalne) - siatkę geograficzną rzutujemy na płaszczyznę styczną do elipsoidy lub przecinającą ją.

• walcowe - siatkę geograficzną rzutujemy na pobocznicę walca stycznego do elipsoidy lub tnącego ją.

• stożkowe - siatkę geograficzną rzutujemy na pobocznicę stożka stycznego do elipsoidy lub tnącego ją.

Odwzorowania kartograficzne pseudoklasyczne (zmodyfikowane):

• Pseudoazymutalne,

• Pseudostożkowe,

• Pseudowalcowe.

TYPY ODWZOROWAŃ (KLASYCZNYCH) ZE WZGLĘDU NA PUNKT PRZYŁOŻENIA POWIERZCHNI RZUTOWANIA

Powierzchnie odwzorowania układa się na różne sposoby względem geometrycznej powierzchni Ziemi:

• ustawia prostopadle do osi ziemskiej lub do płaszczyzny równika ziemskiego, ewentualnie w dowolnym pośrednim położeniu między tymi skrajnymi; w rezultacie otrzymuje się odwzorowania:

• normalne (biegunowe) - kiedy płaszczyzna odwzorowania jest styczna na biegunie lub w przypadku odwzorowań stożkowych i walcowych osie tych brył są zgodne z osią biegunową elipsoidy ziemskiej;

• poprzeczne (równikowe) - kiedy płaszczyzna odwzorowania jest styczna w którymś punkcie na równiku lub osie stożka i walca przechodzą przez płaszczyznę równika

• ukośne (horyzontalne) - kiedy punkt styczności płaszczyzny odwzorowania znajduje się w dowolnym punkcie między biegunami a równikiem lub kiedy osie stożka i walca przechodzą w dowolnym punkcie

• elipsoidy z wyłączeniem biegunów i równika.

ZASTOSOWANIA ODWZOROWAŃ (KLASYCZNYCH) ZE WZGLĘDU NA PUNKT PRZYŁOŻENIA POWIERZCHNI RZUTOWANIA:

• Płaszczyznowe (azymutalne): Służy przede wszystkim do odwzorowywania obszarów okołobiegunowych (położenie normalne), niektórych państw (ukośne), półkul (poprzeczne).

• Stożkowe: Służy głównie do odwzorowywania obszarów w umiarkowanych szerokościach geograficznych (położenie normalne).

• Walcowe: Służy przede wszystkim do tworzenia map stref czasu (położenie normalne) i map topograficznych (poprzeczne).

UKŁADY KARTOGRAFICZNEODZWZOROWANIE GAUSSA-KRUGERA i MERCATORA odwzorowania Gaussa -Krügera i Mercatora są oparte o te same zasady matematyczne. Różnice we współrzędnych pochodzą od inaczej przyjmowanego współczynnika skali:

• w odwzorowaniu Gaussa wiernie odtwarza się południk osiowy; zniekształcenie długości rośnie na zewnątrz, osiągając maksimum na skraju strefy (dla strefy sześciostopniowej zniekształcenie długości wynosi 67 cm na 1 km długości),

• 
  w odwzorowaniu UTM współczynnik skali południka środkowego wynosi 0.9996, na siecznych almukantaratach jest równy 1.0000 i wzrasta w kierunku skraju strefy do 1.0016 (dla pasów sześciostopniowych). W odwzorowaniu UTM zniekształcenia odległości są mniejsze i bardziej równomiernie rozłożone, a zatem powierzchnia elipsoidy jest wierniej odwzorowana na płaszczyźnie niż w odwzorowaniu Gaussa. Współczynnik skali jest prosty w stosowaniu – należy mnożyć przez niego obliczone w odwzorowaniu współrzędne :x0 = x ˇ m,y0= y ˇ m

UKŁADY GEODEZYJNE W POLSCE

DOTYCHCZASOWY SYSTEM ODNIESIEŃ PRZESTRZENNYCH PUŁKOWO'42

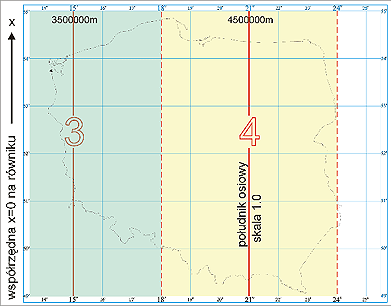
Dawny państwowy układ współrzędnych "1942", powstały przez zastosowanie odwzorowania Gaussa-Krügera elipsoidy Krasowskiego w pasach o szerokości 3° lub 6° (zależnie od celu zastosowania - skali mapy ) i przy założeniu wiernego odwzorowania południka środkowego każdej strefy, czyli ze skalą na południku środkowym mo = 1.0.
Układ obowiązywał w Polsce od roku 1952, ale w służbie cywilnej tylko do drugiej połowy lat 60-tych, od kiedy zaczęto już wprowadzać nowy układ "1965".
Strefy układu "1942" powstałe z odwzorowań pasów 3° , jak również zasada tworzenia współrzędnych pełnych, były analogiczne jak w obecnie wprowadzonym układzie "2000" (zasadnicza różnica kryje się więc w wyborze elipsoidy odniesienia i skali na południkach środkowych). Powstałe układy odwzorowawcze elipsoidy Krasowskiego (odpowiadające pasom 3° z południkami środkowymi: 15°, 18°, 21°, 24° ) oznaczymy odpowiednio: 1942/15 1942/18 1942/21 1942/24
Odwzorowania w pasach 3° stosowano dla map gospodarczych wielkoskalowych.
Odwzorowania w pasach 6° tworzyły w obszarze Polski dwie strefy z południkami środkowymi 15° i 21° . Oznaczymy je odpowiednio (podając dodatkowo informację o szerokości pasa): 1942/15(6) 1942/21(6)

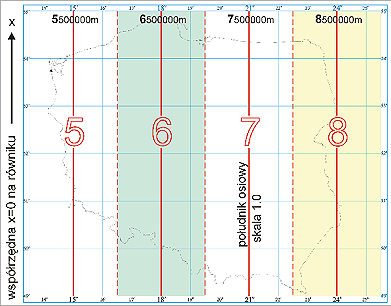
Odwzorowania tego typu stosowano dla map gospodarczych średnio i małoskalowych.
Zasady tworzenia współrzędnych pełnych w układzie 1942:

UKŁADY KARTOGRAFICZNE W POLSCE PSWG'92

PSWG'92 został wprowadzony do stosowania w Polsce Rozporządzeniem Rady Ministrów z dnia 8 sierpnia 2000 r. (DZ.U. nr 70 z dn. 24.08.2000 r. , poz. 821)

Rozporządzenie z dnia 8 sierpnia 2000 wprowadziło do stosowania nowy Państwowy System Współrzędnych Geodezyjnych oparty o Europejski System Odniesień Przestrzennych ETRF'89.W oparciu o nowy system przestrzenny zdefiniowano nowe kartograficzne układy współrzędnych powstałe poprzez aplikacje odwzorowania Gaussa-Krugera elipsoidy GRS'80 (WGS'84). Nowe układy otrzymały nazwy:

1992 (układ jednostrefowy)

2000 (układ czterostrefowy)

UKŁADY WYSOKOŚCIOWE W POLSCE

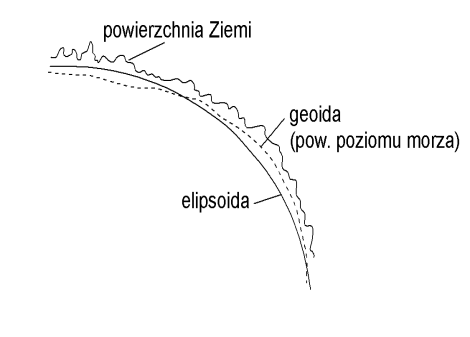
GEOIDA Teoretyczna powierzchnia stałego potencjału siły ciężkości, pokrywająca się z powierzchnią mórz i oceanów Ziemi, przedłużona umownie pod lądami. Kierunek siły ciężkości jest prostopadły do powierzchni geoidy w każdym jej punkcie. Kształt geoidy jest zbliżony do elipsoidy obrotowej, a maksymalne odchylenia od elipsoidy ziemskiej (GRS'80) są rzędu 100 m (na terenach Polski od 28 do 43 metrów). Wyznacza się ją na podstawie pomiarów astronomiczno-geodezyjnych, satelitarnych (altimetria satelitarna), grawimetrycznych i niwelacyjnych.

SYSTEM WYSOKOŚCI NORMALNYCH Państwowym układem wysokości w Polsce jest układ wysokości normalnych zdefinowanych w oparciu o quasigeoidę Mołodieńskiego, odniesionych do średniego poziomu Morza Bałtyckiego w Zatoce Fińskiej, wyznaczonego dla mareografu w Kronstadzie koło Sankt Petersburga (Federacja Rosyjska). H = h -N (B,L)

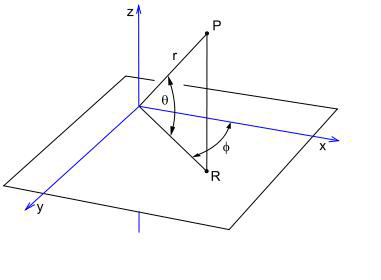
Dwa podstawowe układy współrzędnych: prostokątny i sferyczny

TRIANGULACJA

Metoda określania odległości pomiędzy punktami na powierzchni Ziemi lub ich względnego położenia (lokalny układ współrzędnych) przez pokrycie obszaru siecią połączonych trójkątów.

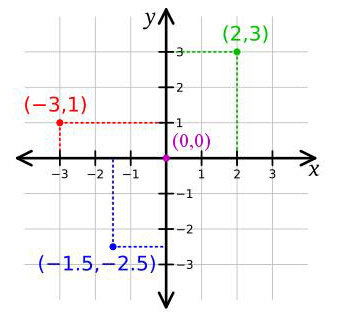
Układ współrzędnych geograficznych

Opisuje położenie punktu na elipsoidzie powstałej przez obrót elipsy wokół osi przebiegającej przez bieguny (najważniejsze elipsoidy: WGS84, GRS80).

Szerokość geograficzna punktu X na powierzchni Ziemi określa kąt między płaszczyzną równika a normalną do płaszczyzny elipsoidy przebiegająca przez ten punkt.

0 - 90 N + / -

0 - 90 S +/ -

Długość geograficzna punktu X na powierzchni Ziemi określa kąt pomiędzy płaszczyzną południka zerowego (wyznacza go elipsa tworząca elipsoidę przebiegająca przez Greenwich) i południka przebiegającego przez punkt X (wyznacza go elipsa tworząca elipsoidę przebiegająca przez ten punkt)

0 - 180 E + / -

0 - 180 W +/-

Siatkę geograficzną tworzą południki i równoleżniki

Równoleżnik - linia (okręgi o różnych promieniach) łącząca punkty o tej samej szerokości geograficznej

Południk - linia (łuk elipsy między biegunami) łącząca punkty o tej samej długości geograficznej

Poziomy i pionowy układ odniesienia:

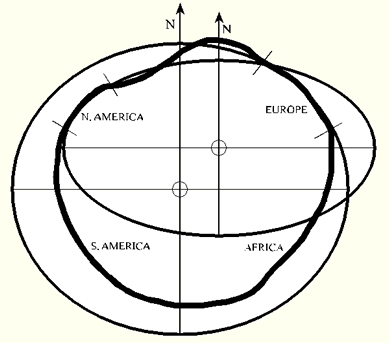
Układ odniesienia (DATUM) oprócz nazwy elipsoidy określa jej położenie względem środka ciężkości Ziemi lub innych punktów. Są układy odniesienia lokalne i globalne.

WGS84 elipsoida WGS 84 (system odniesienia światowy pomiary GPS) geocentryczny

ETRS89 elipsoida GRS 80 geocentryczny (dla Europy!!!!!)

NAD 83 elipsoida GRS 80 geocentryczny

Pułkowo 42 elipsoida Krassowskiego (lokalny Eur. wschodnia)

NAD 1927 elipsoida Clarka (lokalny USA)

ED 87 elipsoida Hayforda (lokalny Europa)

Układy oparte o elipsoidę WGS84/GRS80 są zgodne z dokładnością do 1mm

Czym różni się WGS84 i ETRS89 ?

WGS84 jest przeznaczony dla nawigacji (dokładność 1 m lub mniej). Wersja WGS84 o dużej dokładności jest znana jako ITRS (International Terrestial Reference System) i jest używana w nauce (geofizyka). Istnieje jednak problem z używaniem ITRS (systemu globalnego) do precyzyjnej geodezji. Problemem jest ruch kontynentów (do ok. 12 cm na rok). Cała Europa jest w ruchu względem WGS84 z prędkością około 2.5 cm na rok (10 lat = 25 cm!!!). ETRS89 bazuje na ITRS ale jest dowiązany na stałe do Europy i przemieszcza si względem ITRS (precyzyjnego WGS84). Różnica wynosi aktualnie ok. 40 cm (rośnie 2.5 cm na rok).ETRS89 bazuje na sieci stałych punktów i jest standardem do precyzyjnego GPS.

Poziomy układ odniesienia (DATUM)

Jest określony przez rodzaj elipsoidy oraz sposób jej położenia względem geoidy (lokalny, globalny)

WGS84 elipsoida WGS84 globalny (GPS)

ETRS89 elipsoida GRS80 lokalny (Europa)

NAD83 elipsoida GRS80 lokalny (US)

Pionowy układ odniesienia

1. Względem powierzchni elipsoidy (GPS)

2. Względem powierzchni geoidy = średniego poziomu morza (dawniej Kronsztadt, obecnie EVRS (sprowadzony do NAP - normal Amsterdam peil)

Rodzaj zniekształceń:

1. Kształt - (conformality) dokładna transformacja kątów naokoło punktów (południki i równolezniki przecinają się pod katem prostym)

2. Powierzchnia - dokładna powierzchnia rzutów obiektów

3. Odległość - żadna mapa nie zachowuje odległości (skali) we wszystkich miejscach. Odstępstwo opisuje współczynnik skali (scale factor) iloczyn skala rzeczywista w punkcie/skala mapy

4. Kierunek lub azymut jest kątem liczonym wprawo pomiędzy kierunkiem północnym a innym z danego punktu. Odwzorowania azymutalne (płaszczyznowe) zachowują kierunek dla wszystkich prostych wychodzących z jednego punktu.

Nie ma map bez zniekształceń (co najmniej jeden rodzaj)

Brak zniekształceń możliwy dla punktów lub linii na mapie (południki lub równoleżniki standardowe).

Zniekształcenia mogą być inne w różnych punktach mapy !!!!!

Najważniejsze odwzorowania, układy i systemy współrzędnych:

• UTM (Universal Transverse Mercator) -Uniwersalne poprzeczne Merkatora + UPS ( Universal Polar Stereographic) - Uniwersalne biegunowe stereograficzne

• Wiernopowierzchniowe azymutalne odwzorowanie Lamberta (Lambert Azimuthal Equal Area)

• Konformiczne stożkowe odwzorowanie Lamberta (Lambert Conformal Conical) - Europa, skala kontynentów i oceanów nie więcej niż 90 stopni szer.

• Winkel Tripel (cały glob) - National Geographic Society

• Układ 1992, układ 2000

• Układy 1942, 1965, GUIGiK-1980

UKŁADY WSPÓŁRZĘDNYCH

UKŁAD ORTOKARTEZJAŃSKI

Początek układu może być umieszczony w:

• środku masy Ziemi - geocentryczny

• środku masy Słońca - heliocentryczny

• na powierzchni Ziemi - topocentryczny

Oś Oz - na ogół pokrywa się z osią obrotu Ziemi

Płaszczyzna xOy - leży w płaszczyźnie równika Ziemi lub ekliptyki (płaszczyzna obrotu Ziemi)

Płaszczyzna xOz - dla układów współrzędnych:

• ziemskich - leży w płaszczyźnie umownego południka zerowego (Greenwich

• Niebieskich - leży w płaszczyźnie zawierającej oś Oz i punkt równonocy (punkt przecięcia się ekliptyki z równikiem

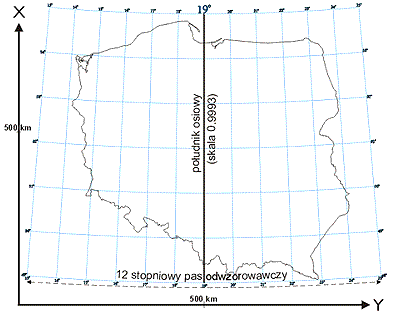
UKŁAD WSPÓŁRZĘDNYCH "1992"

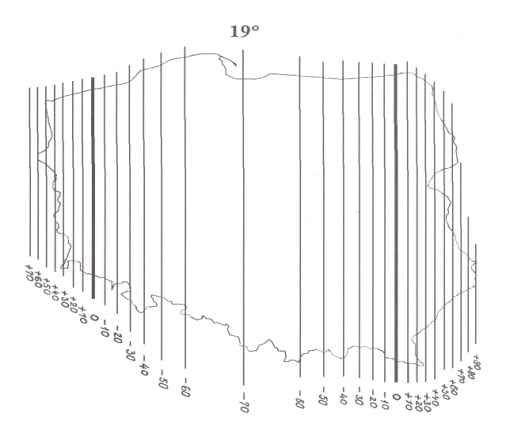
został utworzony w oparciu o jednostrefowe dla obszaru Polski odwzorowanie Gaussa - Krügera elipsoidy GRS-80 z południkiem osiowym (środkowym) Lo=19° i przy założeniu skali długości na tym południku m₀ = 0.9993. Przyjęta skala długości m₀ odwzorowania Gaussa-Krügera ma na celu takie rozłożenie liniowych zniekształceń odwzorowawczych, na obszarze Polski (10^o pas długości geodezyjnej), które wynoszą od -70 cm/km na południku środkowym do ok. +90 cm/km w skrajnych, wschodnich obszarach Polski. Współrzędne pełne w układzie 1992 oblicza się z formuł: X₁₉₉₂ = m₀ • x_GK + x₀, x₀ = - 5 300 000 m i Y₁₉₉₂ = m₀ • y_GK + y₀, y₀ = 500 000 m

Rozkład elementarnych zniekształceń długości W układzie „1992”. Izolinie w odstępach co 10 cm/km

UKŁAD WSPÓŁRZĘDNYCH „2000”

1. Współrzędne płaskie prostokątne x, y są obliczone w odwzorowaniu Gaussa-Krügera w pasach trzystopniowych o południkach osiowych: 15°, 18°, 21°, 24°, ponumerowanych odpowiednio 5, 6, 7, 8.

2. Współczynnik zmiany skali w południku osiowym równa się m₀=0,999923.

3. Obraz równika jest linią o równaniu x=0, a obraz południka osiowego linią o równaniu:

• y = 5 500 000 m dla południka L₀= 15°

• y = 6 500 000 m dla południka L₀= 18°

• y = 7 500 000 m dla południka L₀= 21°

• y = 8 500 000 m dla południka L₀= 24°

Pierwsza cyfra współrzędnej y każdego punktu jest numerem pasa, a jej przemnożenie przez 3 daje długość geograficzną tego pas wyrażoną w stopniach

zniekształcenia liniowe zawierają się w zakresie od −7.7 cm/km na południku osiowym do ok. +7 cm/km na brzegu każdej strefy

Warunek wiernokątności odwzorowania

Odwzorowanie Gaussa-Krügera możemy realizować jako złożenie trzech następujących przekształceń:

1. Wiernokatnego odwzorowania (Lagrange`a) elipsoidy na sferę, jest to przekształcenie; ( B, L) (φ, λ) (λ= L)

2. Wiernokątne odwzorowanie walcowe poprzeczne (Mercatora) ,

3. Wiernokatne przekształcenie płaszczyzny odwzorowania Mercatora w płaszczyznę Gaussa-Krügera

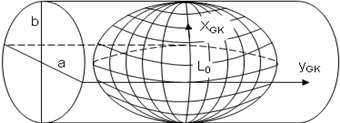
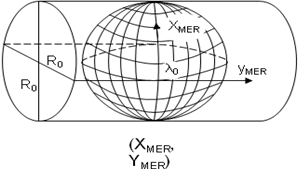
Ziemskie układy odniesienia stosowane w Polsce

Ziemskie przestrzenne systemy odniesienia stosowane w Polsce, można podzielić ze względu na technikę zastosowaną do wyznaczenia współrzędnych punktów definiujących związany z systemem układ odniesienia na: systemy zdefiniowane w epoce w której pomiary wykonywano metodami tradycyjnymi i systemy zdefiniowane w okresie, gdy powszechne zastosowanie znalazły metody kosmiczne i satelitarne. Naturalną konsekwencją tego podziału jest zgodnie z rozważaniami zawartymi w rozdziale 2 niniejszej pracy podział na geocentryczne i niegeocentryczne układy odniesienia.

System odniesienia określony jest poprzez definicję orientacji w przestrzeni osi i położenia początku systemu, a także metrykę (skalę) (Kryński i Rogowski 2004). Przestrzenny system odniesienia może też opisywać elipsoidę odniesienia i odwzorowanie dające współrzędne płaskie stosowane w praktyce geodezyjnej.

Ziemskie układy odniesienia wyznaczone za pomocą klasycznych technik pomiarowych

Powstanie zjednoczonej Polski po rozbiorach spowodowało konieczność wprowadzenia jednolitego układu współrzędnych dla istniejących w trzech zaborach sieci geodezyjnych i map topograficznych. Zadanie to zrealizował Wojskowy Instytut Geograficzny wprowadzając układ odniesienia Borowa Góra (BG).

Układ wpółrzędnych „Borowa Góra”

Układ „BG”, oficjalnie wprowadzony do użytku w 1936 roku, stanowił podstawę prowadzenia prac geodezyjnych i kartograficznych do 1952 roku (Cisak i Sas 2004). Powstał on w wyniku przyłożenia elipsoidy Bessela 1841 (a = 6377395, f = 1/299.152813) do geoidy w Borowej Górze. Orientację zapewniał azymut astronomiczny na wieżę w Modlinie. Jako współrzędne geodezyjne tego punktu przyjęto wyznaczone z pomiarów astronomicznych:

φ = 52º28'32".85 λ = 21º02'12".12

Punkt przyłożenia tego układu znajduje się obecnie na terenie Obserwatorium Geodezyjno-Geofizycznego Instytutu Geodezji i Kartografii w Borowej Górze. Przykryty jest on kopcem o wysokości około 8 m. Punkt ten, pomimo historycznego znaczenia, posiada wyznaczone współrzędne geodezyjne w układzie „65” oraz ITRF.

Współrzędne płaskie punktów sieci geodezyjnej zostały obliczone w odwzorowaniu Roussilhe`a zmodyfikowanym dla terenu Polski przez profesora Grabowskiego z Politechniki Lwowskiej. Odwzorowanie to nazwano odwzorowaniem quasi-stereograficznym Wojskowego Instytutu Geograficznego (WIG). Oficerowie WIG Biernacki i Słomczyński w 1930 roku zastosowali je do opracowania map i współrzędnych punktów triangulacyjnych leżących na obszarze Polski. Punkt główny odwzorowania quasi-stereograficznego WIG obrano w punkcie o współrzędnych: φ = 52°N , λ = 22°E (Greenwich). W celu zminimalizowania zniekształceń na odwzorowywanym obszarze, przyjęto współczynnik zniekształcenia skali m₀ = 0.9995, co daje zerowe zniekształcenia na elipsie zbliżonej do koła o promieniu około 284 km.

Wszystkie mapy wydawane w okresie międzywojennym przez WIG, a także przez niemiecki Sztab Generalny w czasie II wojny światowej (reprinty map polskich), zawierały nadruk siatki współrzędnych w układzie Borowa Góra.

Po drugiej wojnie światowej, w wyniku zmian terytorialnych kraju, do jego części pokrytej przedwojenną osnową geodezyjną dołączona została część pokryta triangulacją niemiecką. Powstała w ten sposób osnowa geodezyjna była niejednorodna (różne elipsoidy odniesienia, różne punkty przyłożenia, różne wyrównania). Na bazie tej osnowy, bez

8 Odwzorowanie quasi-stereograficzne jest odwzorowaniem azymutalnym wiernokątnym, powierzchni elipsoidy (analogia do odwzorowanie stereograficznego powierzchni kuli). Orientacja przestrzenna realizowana jest przez podanie tzw. punktu głównego, który jest punktem styczności z elipsoidą odniesienia płaszczyzny równoległej do płaszczyzny odwzorowawczej. Rozkład zniekształceń liniowych na płaszczyźnie odwzorowawczej, odwzorowania quasi-stereograficznego, definiuje się przez podanie współczynnika zniekształcenia skali w punkcie głównym. przeprowadzenia scisłego wyrównania, obliczono współrzędne geodezyjne punktów w odniesieniu do elipsoidy Bessela 1841 przyłożonej w Borowej Bórze. Współrzędne płaskie w układzie „BG” w odwzorowaniu Gaussa-Krügera zostały obliczone w sześciostopniowych pasach odwzorowczych. Początkowo przyjęto współczynnik zniekształcenia skali na południku osiowym m₀ = 0.999935, a od 1949 roku m₀ = 1 (Różycki 1950). Dokładność wyznaczenia współrzędnych w tym układzie wynosi ok. 0.1 m (Cisak i Sas 2004). Terytorium Polski podzielono na dwie zasadnicze strefy odwzorowawcze: na wschód i na zachód od południka 18 (południki osiowe: 15 i 21).

Układ wpółrzędnych „1965”

• 
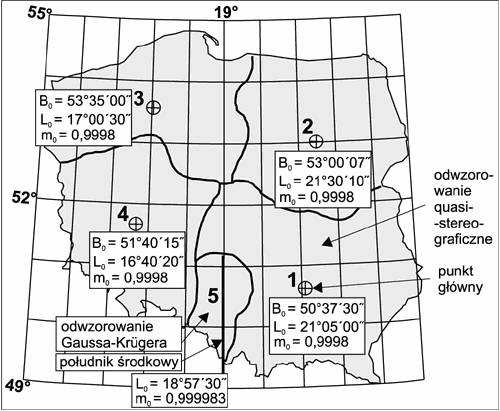
  5 strefowego układu odwzorowawczego

• W strefach 1- 4 zastosowano odwzorowanie quasi-stereograficzne (Roussilhe'a) ze skalą w punkcie głównym (skalę podobieństwa) mo=0.9998.

• Natomiast w strefie 5 - modyfikowane odwzorowanie Gaussa - Krügera o skali na południku środkowym m0 = 0. 999983.

• Zniekształcenia odwzorowawcze w każdej strefie układu mieszczą się w zakresie od 20 cm/km do −20 cm/km. Układ „1965” był przeznaczony głównie do tworzenia mapy zasadniczej.

Dla map topograficznych i przeglądowych w skalach 1:100 000 i mniejszych przyjęto układ oparty na jednostrefowym odwzorowaniu quasi-stereograficznym obszaru Polski nazwany „GUGiK80”. Punkt główny odwzorowania był umiejscowiony w geometrycznym „środku” Polski (φ₀ = 52°10', λ₀ = 19°10'). Współczynnik zniekształcenia skali w tym punkcie wynosi m₀ = 0.999714, a maksymalne zniekształcenie liniowe na granicach Polski wynosi 93 cm/km. Układ ten znalazł zastosowanie jedynie przy opracowaniu wydawanej w latach 1980-1984 topograficznej mapy Polski w skali 1:100 000.

Układ współrzędnych „UTM”

Poprzeczne odwzorowanie Mercatora TM (Transverse Mercator projection) znane również pod nazwą wiernokątnego odwzorowania Gaussa, lub odwzorowania Gaussa-Krügera (van Gysen, 1992) jest walcowym, poprzecznym, stycznym (tj. współczynnik zniekształcenia skali na południku osiowym m₀ = 1), wiernokątnym odwzorowaniem elipsoidy. Do typowych wymiarów pasów odwzorowaczych używanych w odwzorowaniu TM zalicza się pasy 2°, 3°, 4° i 6°. Modyfikacją odwzorowania TM jest uniwersalne poprzeczne odwzorowanie Mercatora UTM (Universal Transverse Mercator projection) stosowane jest na świecie do celów wojskowych i nawigacyjnych od II wojny światowej. Odwzorowanie to stosowane jest przez wszystkie państwa członkowskie NATO. Walec eliptyczny, na powierzchnię którego odwzorowywany jest obraz powierzchni elipsoidy nie jest w wypadku UTM styczny do elipsoidy wzdłuż południka osiowego pasa odwzorowawczego; przecina on elipsoidę w taki sposób, że wzdłuż południka osiowego powstaje stałe zniekształcenie skali m₀ = 0.9996, co odpowiada zniekształceniu liniowemu na południku osiowym −40 cm/km. UTM należy zatem do grupy odwzorowań siecznych elipsoidy. W UTM stosowane są wyłącznie sześciostopniowe pasy odwzorowawcze, którym przypisane są numery wzrastające z zachodu na wschód od 1 do 60, przy czym pas odwzorowaczy o numerze 1 odpowiada strefie odwzorowawczej pomiędzy południkami 180° i 186° (Snyder, 1987). Obszar Polski odwzorowuje się w pasach o numenrach 33 i 34. Odwzorowanie UTM zostało wprowadzone pierwotnie na elipsoidzie Hayforda, obecnie zaś w zastosowaniach cywilnych jak też wojskowych obowiązuje elipsoida WGS84. W Polsce odwzorowanie TM przyjęło się, że nazywać odwzorowaniem Gaussa-Krügera. Sieczne, z wyspecyfikowanym współczynnikiem zniekształcenia skali m₀ ≠ 1, walcowe, poprzeczne, wiernokątne odwzorowanie elipsoidy nazywane jest w Polsce również odwzorowaniem Gaussa-Krügera lub „zmodyfikowanym odwzorowaniem Gaussa-Krügera”.

---