LABORATORIUM WYTRZYMAŁOŚCI MATERIAŁÓW	Imię i Nazwisko:				Grupa: 32 B
Temat ćwiczenia: EULEROWSKIE WYBOCZENIE PRĘTA	Nr ćwiczenia: 1	Data wykonania: 20.10.1999		Data zaliczenia:
	Ocena za sprawozdanie:		Ocena z kolokwium zaliczeniowego:

TEORIA.

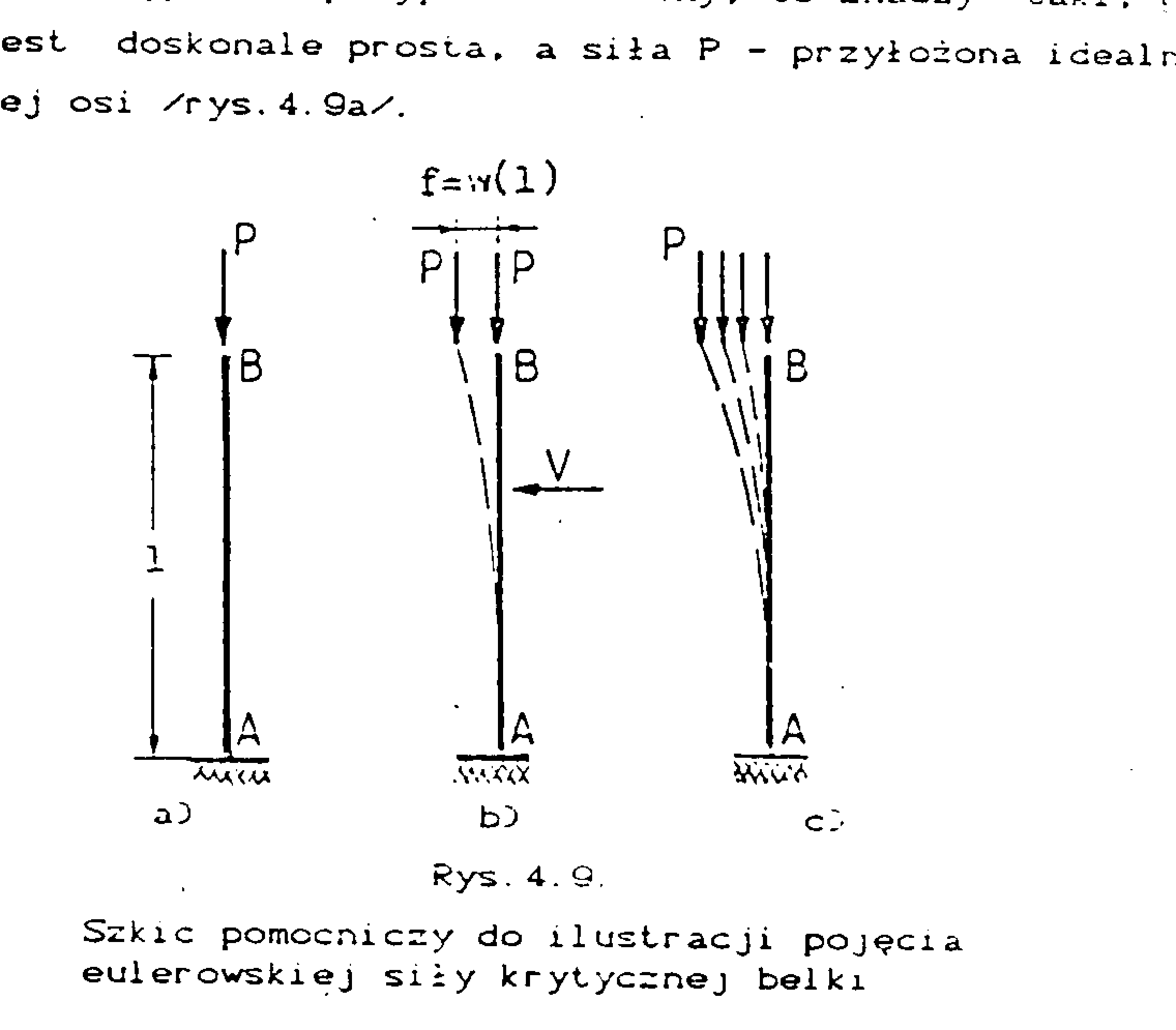
Rysunek 1 przedstawia sposób przyłożenia siły do pręta. Niech siła P rośnie bardzo powoli od zera. Dla każdej jej wartości badamy rodzaj zachodzącej aktualnie równowagi. Robimy to poprzez statyczne przykładanie i zdejmowanie niewielkiego bocznego obciążenia zakłócającego V(rys.1 b). Przy niedużych wartościach P, po wychyleniu pręta z pozycji prostej siłą V, a następnie odjęciu tej siły, pręt samodzielnie wraca do prostej pierwotnie postaci. Jego równowaga jest stateczną (trwałą).

Gdy tę czynność powtórzymy dla kolejno wzrastających wartości P , efekt ten będzie się powtarzał, aż wreszcie - przy pewnej wartości P, nazwanej obciążeniem krytycznym pręt do prostej postaci nie wróci - pozostanie wygięta. Będzie mógł przyjmować każde z położeń określonych strzałką f=w(l) (rys.1 c), łącznie z f=0. Stan równowagi określamy jako obojętny.

Siła krytyczna jest to minimalna siła, przy której pręt (po wyboczeniu z równowagi) pozostaje w równowadze w postaci wygiętej.

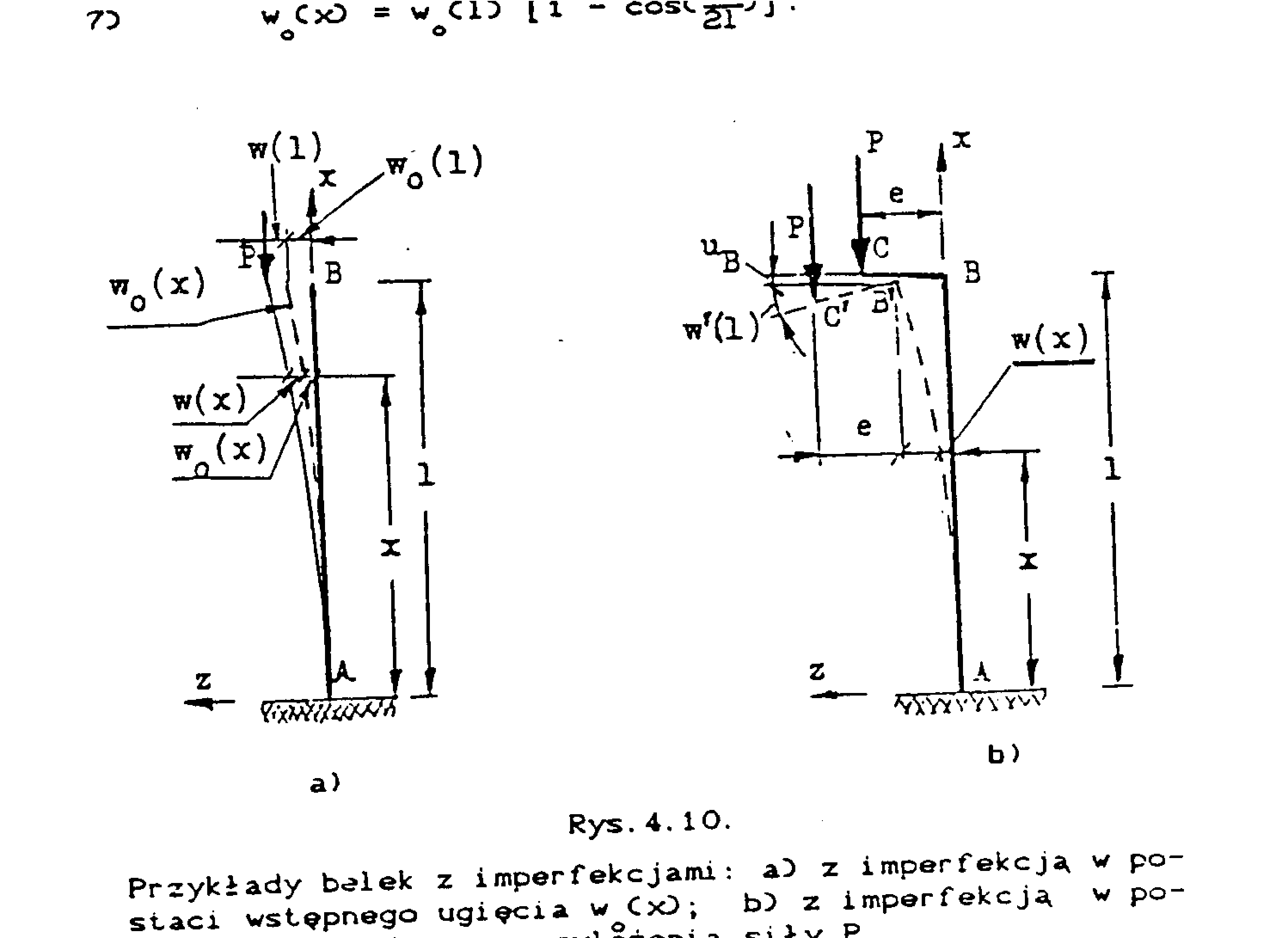
Wykonanie idealnie prostej belki i idealne przyłożenie obciążenia nie jest w rzeczywistości możliwe. Dlatego po przyłożeniu nawet małych obciążeń P ugięcia powstaną natychmiast i próba ujawnienia wartości P_KR opisaną metodą nie doprowadzi do oczekiwanego rezultatu.

Jaki jest sens w ogóle poszukiwania eulerowskich obciążeń krytycznych w sytuacji, gdy zjawisko równowagi w stanie prostym i ugiętym - na skutek istnienia wstępnych niedokładności - nie jest w rzeczywistości realnym? Sens jest, ponieważ - jak wykazują np. analizy przypadków ze wstępnymi defektami (imperfekcjami) - przy wartościach P bliskich P_KR , nawet małe przyrosty ΔP mogą powodować znaczne przyrosty przemieszczeń.

METODA SOUTHWELLA.

Forma otrzymanej zależności (2) jest kluczową dla metody badań w tym ćwiczeniu. Zauważamy, że mierząc ugięcie w(P,x_o) w pewnym punkcie pręta x_o przy znanej sile P, ze wzoru (2) możemy obliczyć P_KR. Dla x=x_o, otrzymuje się warunek:

(3)

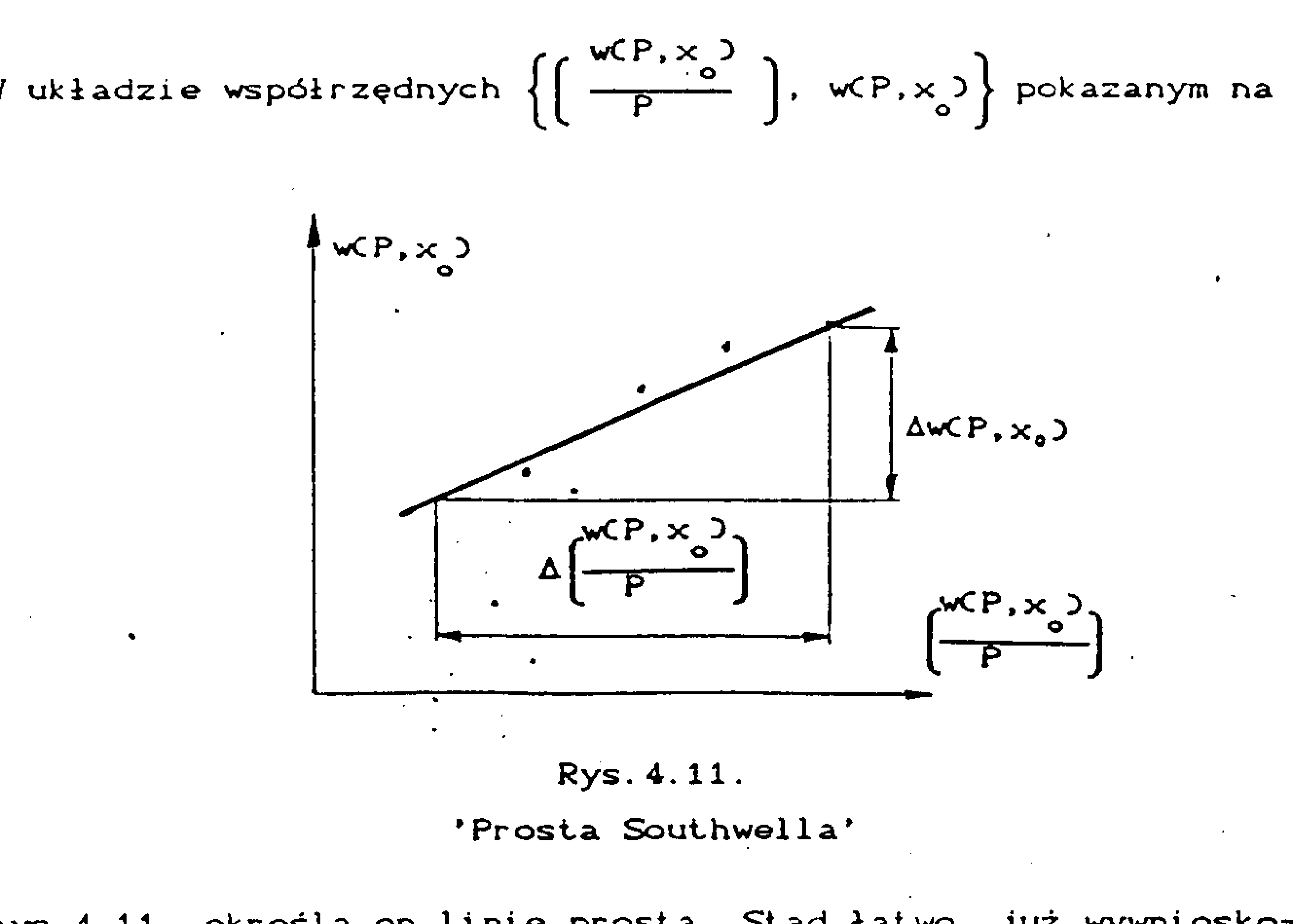
W układzie współrzędnych
pokazanym na rys. 4 określa on linię prostą. Stąd łatwo już wywnioskować, że wielkości mierzone P i w(P,x_o) , odpowiednio przedstawione w tym układzie współrzędnych powinny się układać wzdłuż linii prostej. Wartość siły P_KR jest związana z nachyleniem tej prostej, tzn.

(4)

Wzór (4) oraz całość łączącej się z nim metodyki doświadczalnej podał Southwell. Jak widać, zastosowanie tej metody wymaga spełnienia wielu warunków ograniczających. Przede wszystkim, w trakcie narastania obciążenia P, wstępne pole ugięcia w_o(x) powinno ulegać jedynie pogłębieniu. Korzystanie z zależności (3) i (4) jest uwarunkowane znajomością końcowej postaci ugięcia w(P,x) oraz prowadzenia badań na modelu pręta, który akurat posiada wstępne niedokładności. Inaczej mówiąc, aby korzystać z metody Southwella, należy znać postać funkcji przemieszczeń w(x) w chwili wyboczenia i taką wstępnie nadać badanemu prętowi. Praktycznie można to zrobić np. w ten sposób, że przed rozpoczęciem eksperymentu przykładamy najpierw do belki prostej duże obciążenie P, powodujące znaczne jej ugięcie aż do powstania pierwszych odkształceń plastycznych, a następnie odciążamy.

PRZEKSZTAŁCENIE WZORU.

STANOWISKO POMIAROWE.

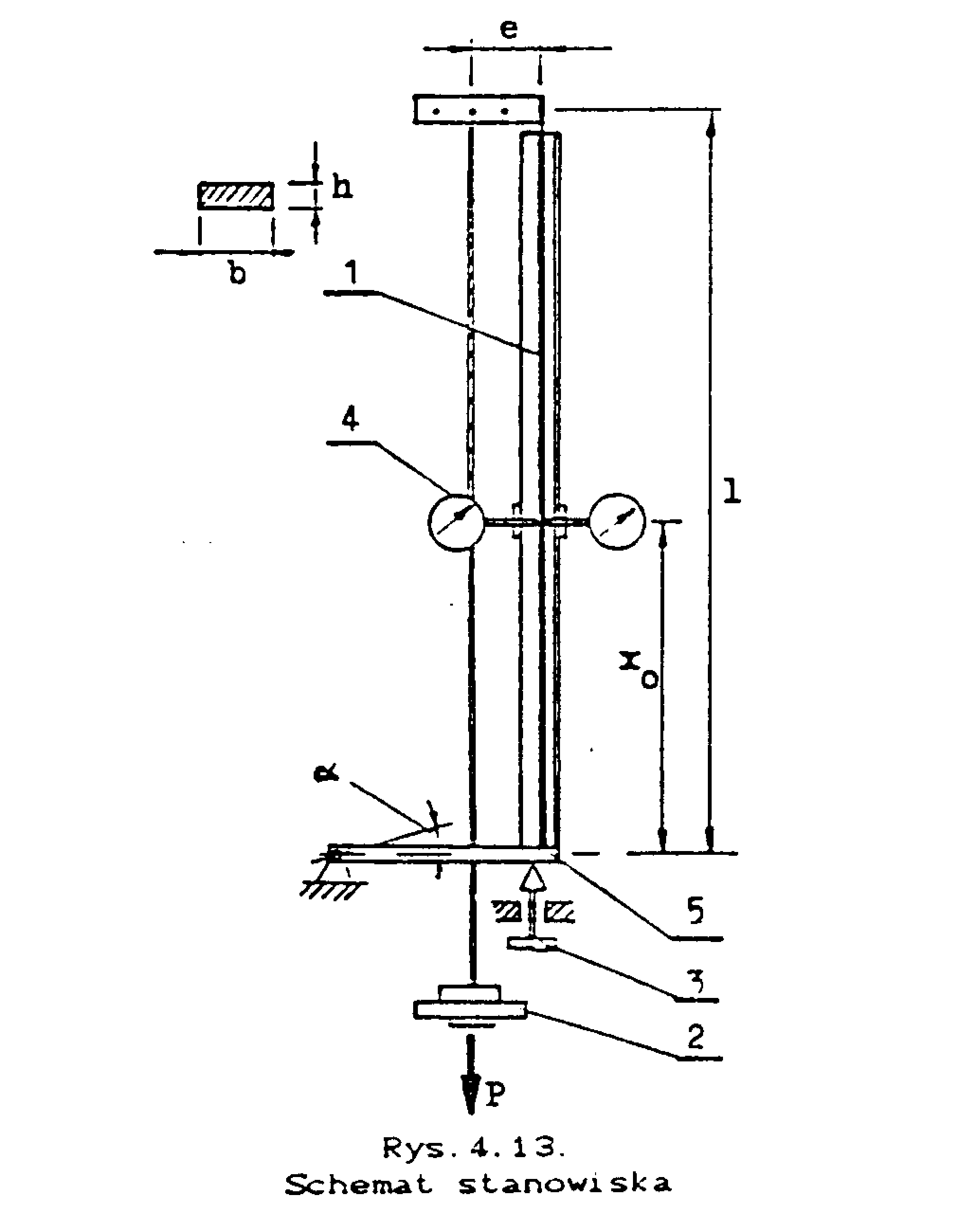
Pręt 1 rys.5 dla którego wyznaczamy siłę krytyczną jest utwierdzony w końcu dolnym, w górnym zaś - obciążony siłą P przyłożoną na mimośrodzie e, który można skokowo zmieniać. Siłę P przykłada się obciążając szalkę ciężarkami 2. Cały układ podparcia 5 wraz z modelem pręta 1 można pochylić (śruba 3) o niewielki kąt, uzyskując tym samym sztuczne wymuszenie ugięcia pręta niewielką składową poprzeczną obciążenia P. Również przy takiej imperfekcji przyłożenia siły otrzymuje się dobre przybliżenie wyznaczanego obciążenia krytycznego. Ugięcia w(x) mierzone są za pomocą czujników zegarowych 4.

Pomiary przeprowadzamy dla trzech wartości mimośrodu e i trzech wartości obciążenia P. (dla każdego e). Układ pomiarowy jest ustawiony poziomo. Obciążenia szalek dobieramy w ten sposób aby ugięcia mierzone czujnikami zawierały się w granicach 1-9mm. Długość badanego pręta wynosi l=1000mm, wymiary poprzeczne b*h=13*5. Mimośrody - e=8,16,24mm. Przemieszczenia są mierzone w punkcie x_o=l/2.

OBLICZENIE TEORETYCZNEJ SIŁY KRYTYCZNEJ.

PRZEBIEG I WYNIKI

Działamy na pręt siłą przyłożoną na mimośrodzie. W kolejnych trzech pomiarach zmieniamy wartość mimośrodu i tak kolejno e=8, e=16, e=24. Na obciążniku zawieszamy kolejno szalki, które stanowią zwiększenie obciążenia. Odczytujemy z obu wskaźników wartości odchylenia pręta. Następnie porównujemy je z wartością zerowaną i obliczamy wartość średnią, która jest równa W.

P [N]	Ol	Op	W	W/P
e=24
0	1,1	9,14
8	2,99	7,23	1,9	0,23
14,8	5,38	4,81	4,305	0,29
21,6	8,99	1,18	7,905	0,366
e=16
0	1,1	9,14
8	2,19	8,04	1,095	0,136
14,8	3,97	6,24	2,885	0,194
21,6	6,28	3,9	5,21	0,241
e=8
0	1,27	8,97
8	1,68	8,55	0,415	0,051
14,8	2,68	7,53	1,425	0,096
21,6	4,11	6,1	2,885	0,132

PORÓWNANIE SIŁY KRYTYCZNEJ Z WYKRESU Z SIŁĄ TEORETYCZNĄ.

Pkr (obliczeniowa) = 66,74 N

Pkr (z wykresu) = 44,295 N; 38,88 N; 29,809 N

WNIOSKI.

Z przeprowadzonych badań wynika, że siła krytyczna obliczeniowa nie jest równa co do wartości sile krytycznej odczytanej z wykresu. Siły odczytane z wykresu dla trzech serii pomiarów także różnią się od siebie. Możemy wywnioskować ,że duże różnice między Pkr (obliczeniową) ,a Pkr (z wykresu) są spowodowane błędnymi odczytami z czujników.

Rys.4

Rys.3

Rys.2

Rys.1

Rys.5

Smukłość

---