ŚWIATŁO JAKO FALA

• Wiele zjawisk w optyce nie można wytłumaczyć stosując opis geometryczny. Opis ten można traktować jako pewne przybliżenie, ale do dokładnej analizy konieczne jest zastosowanie opisu falowego.

• Z równań Maxwella możemy otrzymać tzw. równanie falowe:

,

(dla ośrodka nieprzewodzącego!), którego rozwiązaniem ogólnym jest:

gdzie:
jest amplitudą fali (ogólnie: zespolona!), a wyrażenie w nawiasie cosinusa nazywamy fazą fali.

FALA PŁASKA

• Rozwiązaniem szczególnym równania falowego jest fala płaska:

gdzie:

- to amplituda fali;

- to faza fali;

- to częstość fali (zwana też częstością kołową);

- to liczba falowa (można ją też traktować jako wektor);

- to okres drgań (okres fali);

- to faza początkowa;

- to długość fali.

FALA KULISTA

• Innym często spotykanym w praktyce rozwiązaniem jest fala kulista:

• Powierzchnie stałej fazy nazywamy frontem falowym.

• Mierzalną wielkością jest energia fali świetlnej, proporcjonalna do kwadratu amplitudy natężenia pola elektrycznego. Ponadto wszystkie detektory dokonują uśrednienia czasowego. Natężeniem światła nazywamy wielkość:

INTERFERENCJA FAL

• Nakładanie się fal nazywamy ogólnie superpozycją.

• Nakładanie się spójne (koherentne) fal - interferencja.

Źródła spójne - drgające zgodnie w fazie albo takie, dla których fazy wiążą się ze sobą w określony sposób (przesunięcia fazowe między wiązkami nie powinny podlegać zbyt szybkim zmianom).

• Interferencja polega na nałożeniu się dwóch fal z ich fazami i amplitudami - koherentne (spójne) - w odróżnieniu od „zwykłego” nałożenia się natężeń tych fal w przypadku źródeł niespójnych.

• (Jeszcze raz!) Światło jako fala elektromagnetyczna ma częstotliwość tak dużą, że każdy detektor rejestruje uśrednioną w czasie (< >) wartość natężenia I, a więc:

Jeśli nakładające się fale nie są w żaden sposób zgodne w fazie, średnia czasowa „traci” informację o fazach tych fal.

INTERFERENCJA DWÓCH FAL

• Interferencja fal z dwóch źródeł punktowych:

Rozważmy dwa jednakowe punktowe źródła fal EM (sinusoidalnych). Wypadkowe pole EM obserwujemy na ekranie w punkcie D. Załóżmy, że oba źródła wysyłają płaskie fale monochromatyczne (o jednakowej częstości) o jednakowej fazie początkowej i jednakowej amplitudzie. (Wektory elektryczne musza mieć też ten sam kierunek, to znaczy stan polaryzacji obu fal musi być taki sam!)

• Zakładamy też, że obie fale biegną w tym samym ośrodku, bo inaczej:

Równania obu fal mają postać:

INTERFERENCJA DWÓCH FAL - c.d.

• Falę wypadkową obliczymy, korzystając z tożsamości:

• Po dodaniu obu fal, otrzymujemy:

gdzie:

Otrzymujemy więc falę o tej samej częstości
co każda z fal składowych i amplitudzie zależnej od
.

• Natężenie światła w punkcie D:

INTERFERENCJA DWÓCH FAL - c.d.²

• Używając pojęcia drogi optycznej można zapisać natężenie inaczej:

gdzie
jest różnicą faz obu fal.

• W wyniku dodania dwóch spójnych, monochromatycznych fal płaskich otrzymaliśmy falę, której natężenie może się zmieniać od
do
. Taki właśnie rodzaj nakładania się fal nazywamy interferencją.

• Powierzchnie jednakowego natężenia światła - prążki interferencyjne - są opisane równaniem
, czyli:

gdzie wskaźnik
nazywany jest rzędem interferencji.

INTERFERENCJA DWÓCH FAL - c.d.³

• Maksima interferencyjne (jasne prążki) powstają w miejscach, gdzie rząd interferencji jest całkowity:

• Minima interferencyjne (ciemne prążki) powstają w miejscach, gdzie rząd interferencji jest połówkowy:

• Kształt prążków interferencyjnych powstałych w wyniku dodawania się dwóch fal kulistych określa równanie:

INTERFERENCJA DWÓCH FAL KULISTYCH

• W przypadku fal kulistych, kształt prążków zależy od położenia ekranu względem źródeł obu fal - prążki mają kształt krzywych stożkowych.

FALE O RÓŻNEJ AMPLITUDZIE

• Nasze rozważania możemy uogólnić: niech teraz fale składowe mają różne amplitudy. Zagadnienie można rozwiązać, korzystając z tożsamości trygonometrycznych bądź korzystając z metody wykresów wskazowych.

• Obliczone wypadkowe natężenie światła wyraża się teraz wzorem:

Jest to podstawowy wzór interferencyjny.

Interferencyjna suma dwóch fal ma natężenie równe sumie natężeń fal składowych, powiększonej o człon interferencyjny, który może mieć wartość dodatnią (wzmocnienie) lub ujemną (wygaszenie).

FALE O RÓŻNEJ AMPLITUDZIE - c.d.

• Jasne prążki interferencyjne powstają wtedy, gdy:

,

a natężenie światła osiąga wtedy maksymalna wartość równą:

• Ciemne prążki interferencyjne powstają wtedy, gdy:

,

a natężenie światła osiąga wtedy maksymalna wartość równą:

FALE O RÓŻNEJ AMPLITUDZIE - c.d.²

• Widzialność obserwowanych prążków zależy od zależności między maksymalna i minimalna wartością natężenia światła w obrazie interferencyjnym. Miarą widzialności jest kontrast wizualny:

,

który w przypadku rozważanych prążków wynosi:

DOŚWIADCZENIE YOUNGA (1802)

• Eksperyment, który pokazuje praktyczny sposób uzyskania interferencji fal. Rolę „dwóch źródeł” pełnią dwa otwory, oświetlone przez jedno źródło - pozwala to na spełnienie warunku spójności.

Dwie interferujące fale powstają dzięki podziałowi czoła fali. Pochodzą one z jednego źródła, więc mają tę samą częstotliwość i fazę początkową.

• W oryginalnym doświadczeniu Younga szczeliny były liniowe - a więc każda z nich była (zgodnie z zasadą Huyghensa) źródłem fali walcowej.

DOŚWIADCZENIE YOUNGA - c.d.

• Jak już wiemy, natężenie światła w obrazie interferencyjnym zależne jest od różnicy faz
nakładających się fal. Różnica faz zależy od różnicy dróg promieni
i
:

gdzie:

i

W celu wyliczenia różnicy faz skorzystamy z rozwinięcia:

,

i założymy, że:
(odległość dwóch „źródeł” od ekranu jest dużo większa, niż odległość między nimi).

DOŚWIADCZENIE YOUNGA - c.d.²

• Różnica faz, obliczona przy zastosowaniu założonego przybliżenia dalekiego pola (Fraunhofera):

• Rozkład natężenia światła na ekranie, odległym o
jest więc dany równaniem:

Odległość między prążkami na ekranie jest równa:

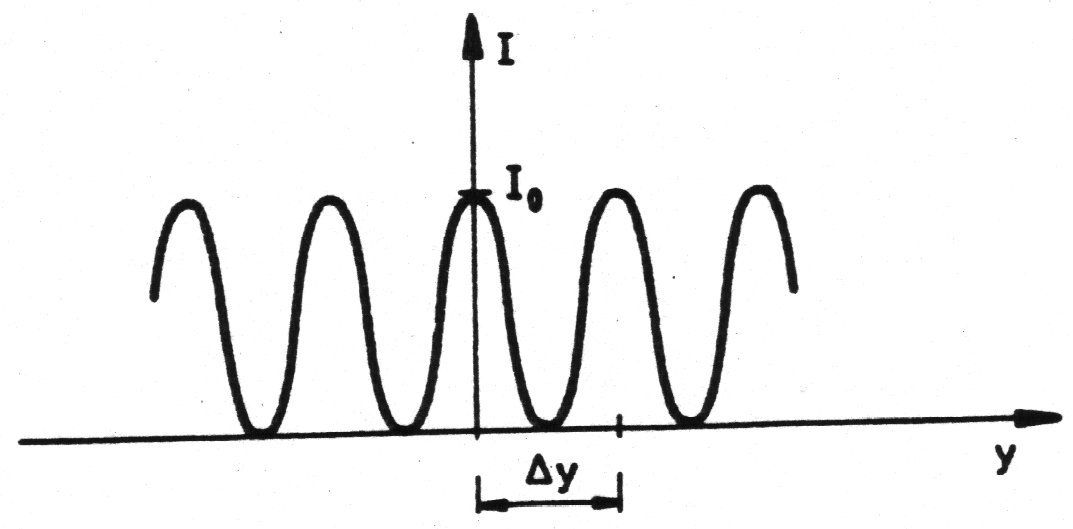
KOHERENCJA ŚWIATŁA

• Dlaczego w doświadczeniu Younga użyto dwóch szczelin jako wtórnych źródeł światła? Załóżmy, że zamiast tego, użyjemy dwóch niezależnych źródeł, o różnych częstotliwościach i fazach początkowych:

(dla uproszczenia przyjęto równość amplitud obu fal).

• Fala wypadkowa będzie miała postać:

gdzie:

częstość fali wypadkowej:

faza:

a najważniejsza (z punktu widzenia odbieranego natężenia!) amplituda...

KOHERENCJA ŚWIATŁA - c.d.

• Amplituda fali wypadkowej zależy od czasu:

Natężenie to średnia czasowa z kwadratu amplitudy tej fali:

• Dla różnych częstości obu fal, średnia czasowa jest równa:

A więc:

• Dla fal o niejednakowych amplitudach otrzymalibyśmy:

Czyli: Jeżeli nakładające się fale mają różne częstotliwości, to wypadkowe natężenie światła pulsuje z częstością
i nie obserwujemy obrazu interferencyjnego - natężenie obu fal dodaje się algebraicznie.

KOHERENCJA ŚWIATŁA - c.d.²

• Załóżmy teraz, że obie fale mają tę samą częstotliwość, ale pochodzą z całkowicie niezależnych źródeł - emitowane są wtedy ciągi falowe o różnych (skończonych) długościach i przypadkowo zmieniających się fazach początkowych. Oznacza to, że składnik fazowy:

jest wielkością losową, czyli średnia czasowa jest równa:

• Takie fale są więc również niespójne - obserwujemy „zwykłe” sumowanie natężeń i brak zmiennego rozkładu natężenia („prążków interferencyjnych”).

• W praktyce nie ma możliwości uzyskania interferencji przy nakładaniu się fal świetlnych z niezależnych źródeł - głównie ze względu na dużą częstotliwość fal świetlnych i skończony czas detekcji (uśrednianie).

KOHERENCJA PRZESTRZENNA

• Powtórzmy doświadczenie Younga ale z rozciągłym źródłem światła - to znaczy takim, którego rozmiary poprzeczne będą być może grały rolę w powstawaniu obrazu interferencyjnego.

• Rozważmy obraz interferencyjny pochodzący od dwóch punktów źródła: środkowego
i skrajnego
. Na ekranie powstają dwa układy prążków interferencyjnych. Fazy początkowe fal wychodzących ze szczelin
i
nie są teraz jednakowe. Dodatkowa różnica faz jest równa:

KOHERENCJA PRZESTRZENNA - c.d.

• Powtarzając schemat obliczeń (przybliżenie!) jak w przypadku źródła punktowego, znajdziemy wyrażenie na dodatkową różnicę faz:

• Uwzględniając tę dodatkową różnicę, otrzymamy ostatecznie formułę na rozkład natężenia światła na ekranie:

Prążki interferencyjne są więc identyczne do tych, które powstają z punktowego źródła, są również tak samo odległe względem siebie, ale są przesunięte względem prążków utworzonych przez centralny punkt źródła o:

KOHERENCJA PRZESTRZENNA - c.d.²

• Przesunięcie wzajemne obu układów prążków ilustruje wykres:

• Rozciągłe źródło światła składa się z wielu punktów świecących - każdy z nich da podobny układ prążków, który na powyższym wykresie będzie się znajdował pomiędzy oboma układami. Rozkłady natężeń wszystkich prążków dodają się i powodują w efekcie rozmycie, obniżające kontrast prążków. Efekt ten nazywamy niekoherencją (częściową koherencją) przestrzenną promieniowania.

• Całkowite rozmycie nastąpi, gdy skrajne układy prążków ułożą się w ten sposób, że maksimum jednego przypada na minimum drugiego. Doprowadzi to do warunku:

KOHERENCJA CZASOWA

• Przeanalizujmy teraz wpływ niemonochromatyczności źródła światła - jak już wiadomo, źródła termiczne promieniują skończone ciągi falowe, które mogą być uznane za nie w pełni monochromatyczne.

• Niech teraz punktowe źródło wysyła dwie fale o niewiele się różniących częstościach:
i
(długościach
,
). Na ekranie powstaną znowu dwa niezależne układy prążków, ułożonych symetrycznie względem szczelin
i
, ale różniących się odległością międzyprążkową (która zależy od
!).

• Rozkłady intensywności w obu obrazach interferencyjnych dane są znanym już wzorem:

KOHERENCJA CZASOWA - c.d.

• Granicznym warunkiem, który spowoduje całkowite rozmycie prążków, może być znowu kryterium pokrywania się maksimum jasnego prążka
-tego rzędu dla jednej długości fali i ciemnego prążka
rzędu dla drugiej. Prowadzi to do zależności:

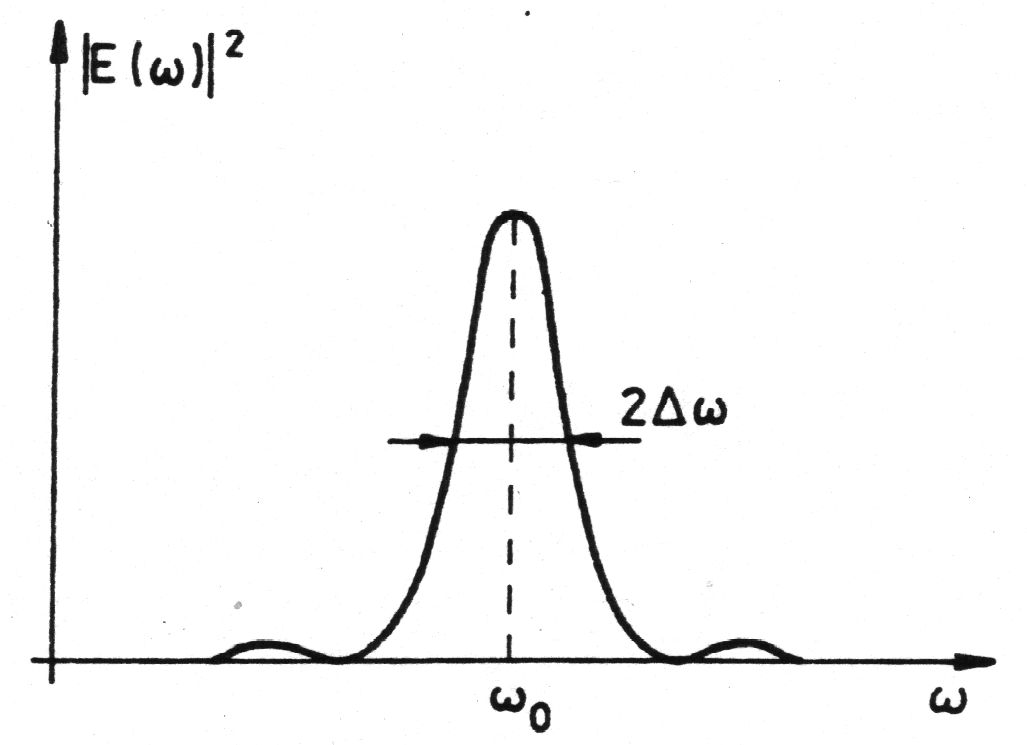
• Dla niewiele się różniących długości fal (o
) można posłużyć się pojęciem średniej długości fali
i szerokości spektralnej
. Wtedy:

gdzie
oznacza numer prążka, dla którego kontrast maleje do zera. Oznacza to, że jeżeli światło zawiera fale z przedziału o szerokości
, to obraz interferencyjny jest widoczny dopóki różnica dróg optycznych nie przekroczy
. Tę odległość nazywamy długością (drogą) koherencji.

KOHERENCJA CZASOWA - c.d.²

• Inny sposób na zrozumienie pojęcia drogi koherencji to przypomnienie faktu, że nie istnieje fala dokładnie monochromatyczna. Mamy do czynienia zawsze z ciągiem falowym („paczką falową”) o średniej częstości
i skończonym czasie trwania
. Taki ciąg falowy równoważny jest (analiza fourierowska!) mieszaninie fal monochromatycznych o częstościach z zakresu
. Wielkość
proporcjonalna jest do czasu
, zwanym czasem koherencji:

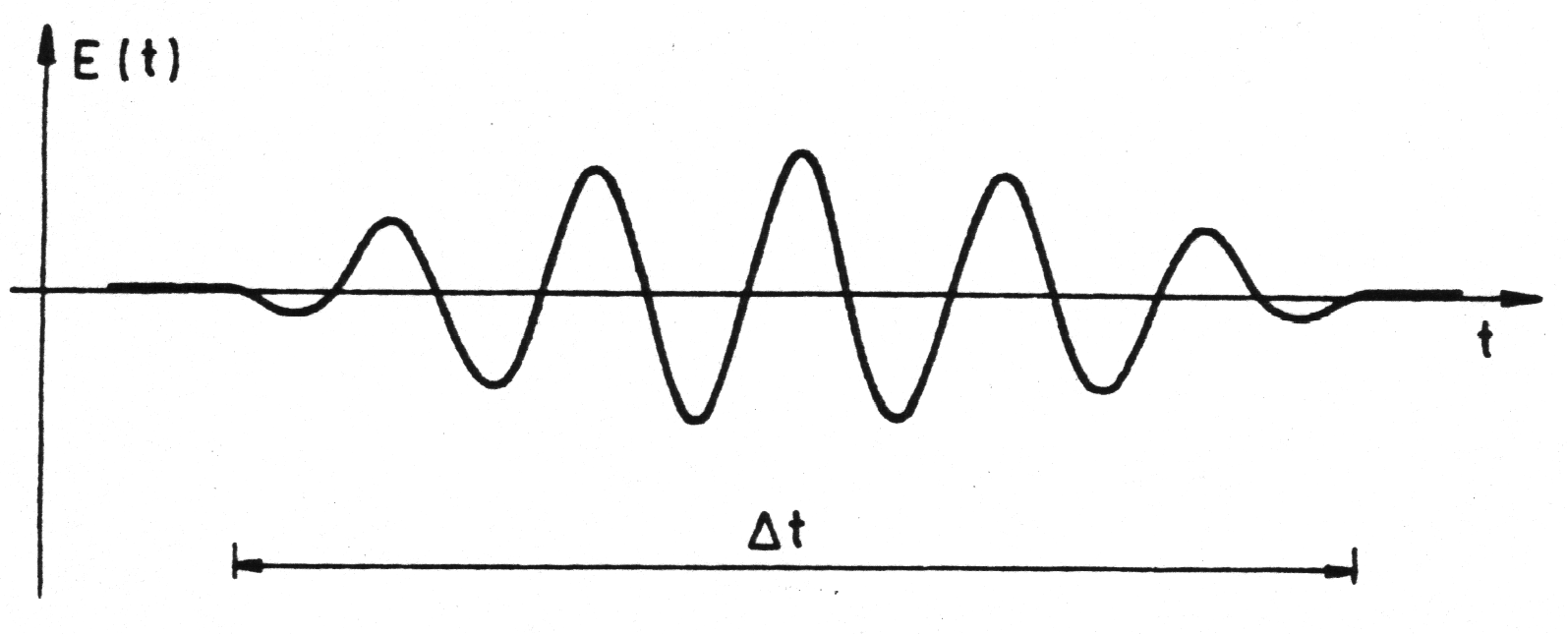
KOHERENCJA CZASOWA - c.d.³

• Czas trwania ciągu falowego („paczki”) i jego długość są ze sobą związane:

• Fala świetlna emitowana przez typowe źródła termiczne składa się z szeregu ciągów falowych, wysyłanych po sobie z różnymi, przypadkowymi fazami. Po podzieleniu takiej fali na dwie (jak w doświadczeniu Younga) i ponownym nałożeniu (interferencji) obserwujemy obraz interferencyjny tylko wtedy, gdy nałożą się na siebie odpowiednie ciągi falowe. Tak więc różnica dróg optycznych, wprowadzana przez układ interferencyjny, nie może być większa od długości ciągu falowego. Tę właściwość fali świetlnej nazywamy częściową koherencją.

INTERFERENCJA - PRZYKŁADY

• Interferencja w klinie - prążki równej grubości:

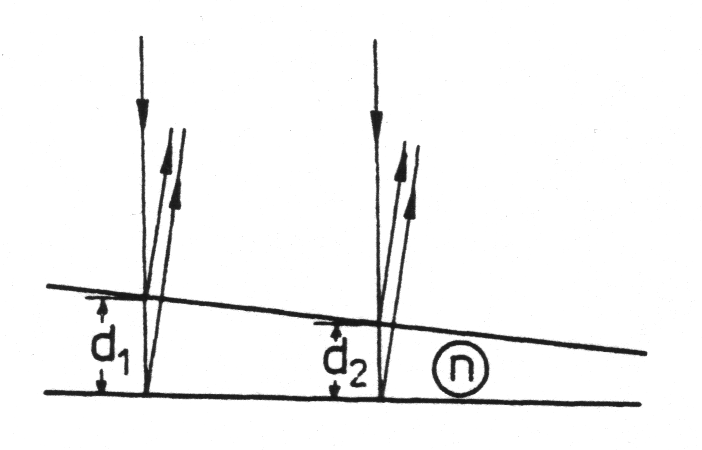
• Odmiana prążków równej grubości: pierścienie Newtona

INTERFERENCJA - PRZYKŁADY - c.d.

• Interferencja w płytce płasko-równoległej

- prążki równego nachylenia

Różnica dróg optycznych między promieniami, odbitymi obu powierzchni płytki:

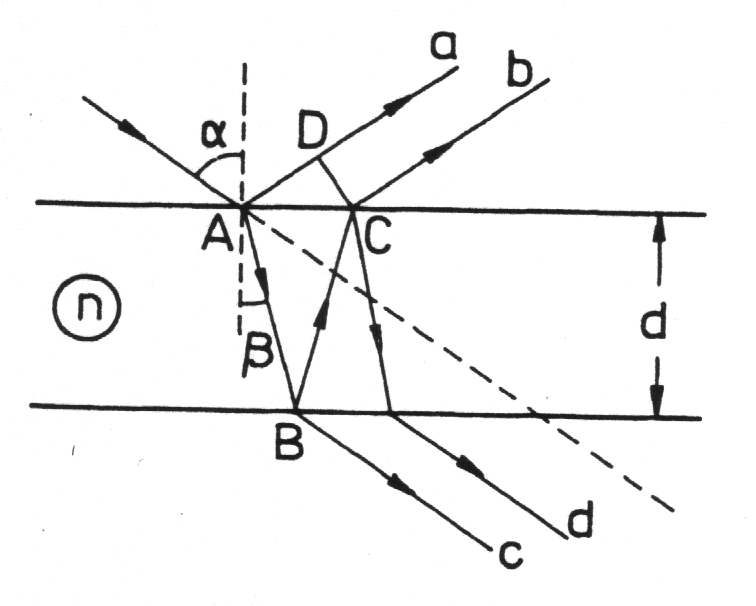
jeśli:
nastąpi

wzmocnienie

Przykład: barwy interferencyjne baniek mydlanych.

INTERFERENCJA - PRZYKŁADY - c.d.

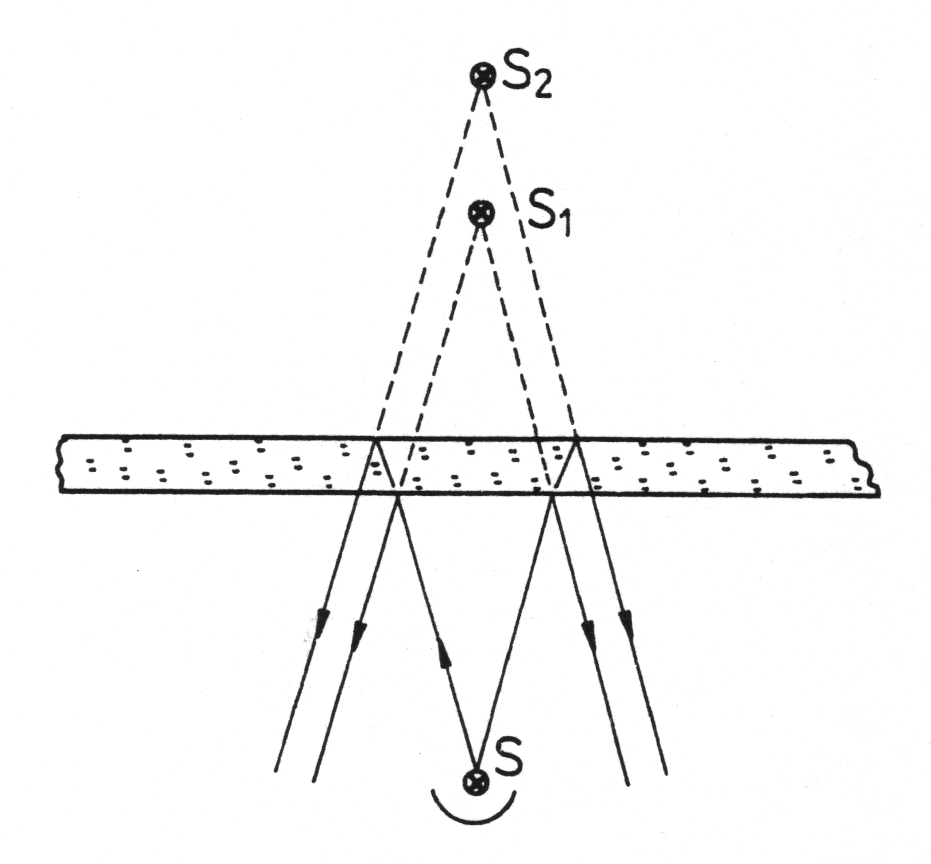
• Doświadczenie Pohla:

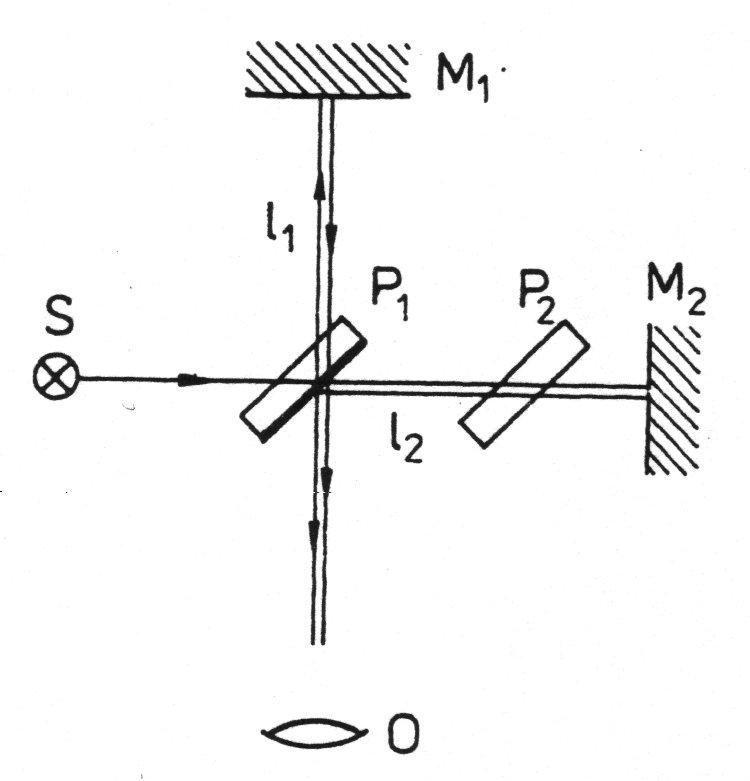
• Interferometr Michelsona

- dawna definicja wzorca długości:

1 m =1 650 763,73 długości fali czerwonej linii

(obecnie: odległość, jaką przebywa światło w 1/299 792 458 sek)

INTERFERENCJA WIELU FAL

• W wielu przypadkach mamy do czynienia z dodawaniem większej liczby płaskich fal składowych. Obraz interferencyjny będzie teraz bardziej złożony.

SIATKI DYFRAKCYJNE

• Układ równoległych, równoodległych szczelin (niekoniecznie szczelin...), w którym odległość d między szczelinami, tzw. stała siatki, jest porównywalna z długością fali.

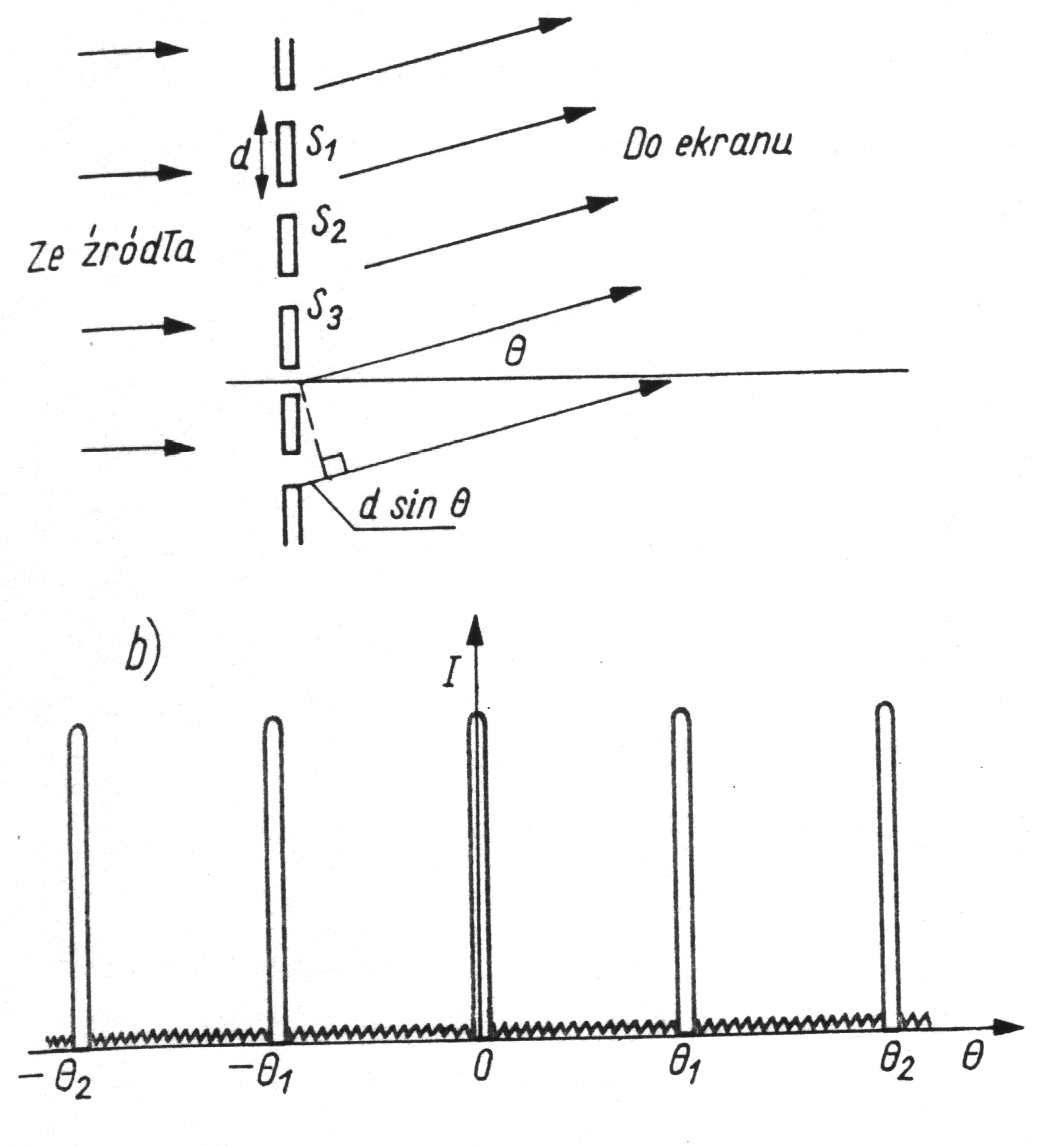
Natężenie na ekranie:

gdzie:

Maksima dla:

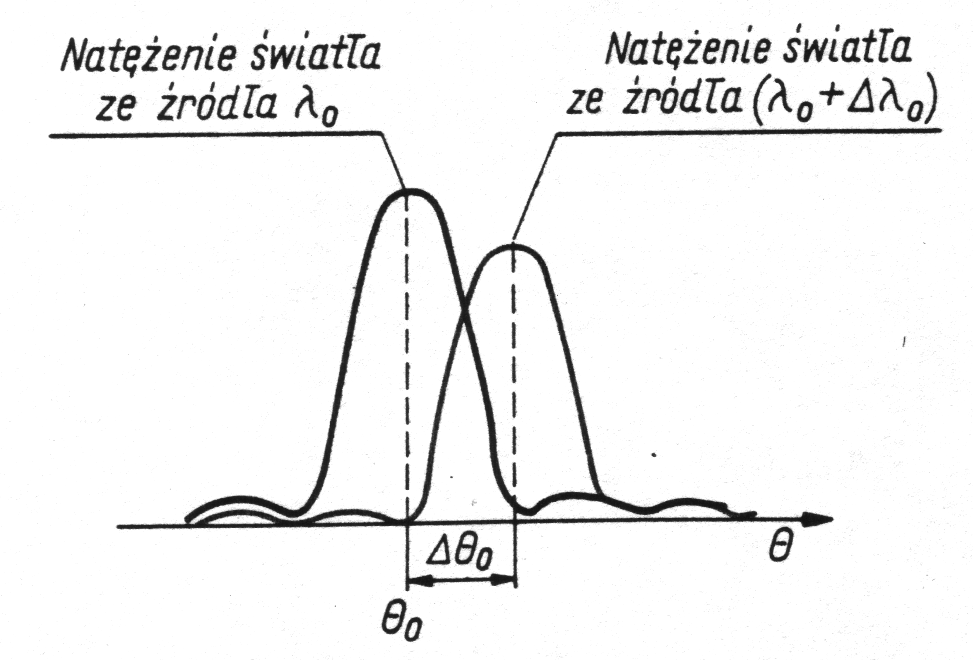
Zdolność rozdzielcza:

(m - rząd widma)

INTERFERENCJA WIELOKROTNA

• Interferometr Fabry'ego-Perota:

Amplitudowy współczynnik przepuszczania:

Amplitudowy współczynnik odbicia:

Natężeniowy (energetyczny) współczynnik przepuszczania:

Natężeniowy (energetyczny) współczynnik odbicia:

Przy braku absorpcji:

INTERFERENCJA WIELOKROTNA - c.d.

• Wielokrotne przejście fali świetlnej przez układ interferometru Fabry'ego-Perota:

• skoki fazy o π przy każdym odbiciu wewnątrz zwierciadeł;

• każde przejście fali między zwierciadłami to zmiana fazy o:
  .

• Gdy efektywna grubość warstwy równa jest połowie długości fali:

to można pokazać, że światło w ogóle nie odbija się od takiego układu (
) a więc jest to warstwa przeciwodblaskowa.

• Natężenie światła przepuszczonego przez układ:

INTERFERENCJA WIELOKROTNA - c.d.²

• W przypadku dopasowania różnicy faz, gdy:

całe światło przechodzi przez układ. Dla ustalonej odległości
między zwierciadłami i ustalonego kąta padania
(zwykle: prostopadle) zachodzi to dla tych długości fal świetlnych, które spełniają warunek:

Dla innych długości natężenie światła przepuszczanego przez układ szybko spada - zależy to od wartości współczynnika
:

Kontrast prążków:

33

---