Zajęcia 1

Zmienna losowa

1. skokowe (dyskretne)

2. ciągłe

Wybrane rozkłady

1. skokowe

2. ciągłe

Ćwiczenia

Rozkład normalny

Definicja

Zmienna losowa ciągła ma rozkład normalny, jeśli funkcja gęstości określona jest wzorem

,

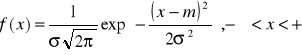
gdzie m i σ >0 są parametrami

Ciągła zmienna losowa X ma rozkład normalny o wartości oczekiwanej m (μ) i odchyleniu standardowym σ, oznaczamy X~N(m,σ²) lub X~N(m,σ)

Definicja

Rozkład normalny ze średnią m=0 i odchyleniem standardowym σ=1 nazywamy standardowym rozkładem normalnym i oznaczamy Z~N(0,1)

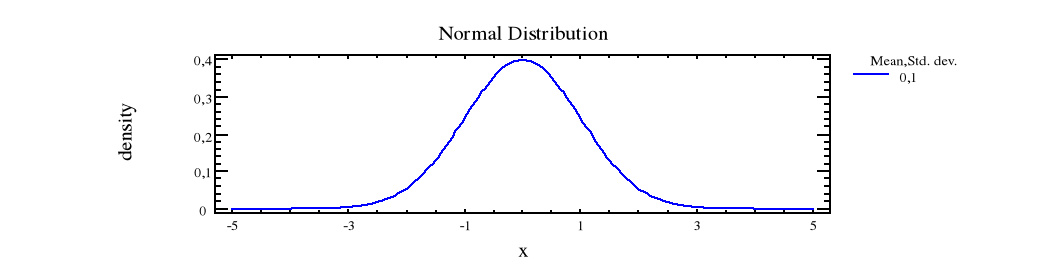
Wykres funkcji gęstości określany jako krzywa normalna ma charakterystyczny kształt dzwonu

Własności krzywej:

1. Jest symetryczna względem prostej z=0

2. Osiąga maksimum równe dla z=0

3. Posiada dwa punkty przegięcia dla z=1 i z=-1

Standaryzacja zmiennych - jest to przekształcenie (transformacja) wartości zmiennej wg następującego wzoru:

gdzie: m- średnia, σ- odchylenie standardowe, X- wartość zmiennej przed standaryzacją,

Z- wartość zmiennej po standaryzacji; zmienna po standaryzacji ma rozkład normalny Z~N(0,1).

Polecenie 1

Wykonanie w programie Statgraphics wersja 4.1

1. funkcja gęstości p-stwa rozkładu normalnego standardowego (o średniej 0 i odchyleniu standardowym 1)

2. na tym samym wykresie zaznaczyć funkcje gęstości zmiennych o rozkładzie normalnym zmieniając ich:

1. wartość średnią N(3,1); N(5,1)

2. wartość odchylenia standardowego N(3,2); N(5;0,5)

ad 2a

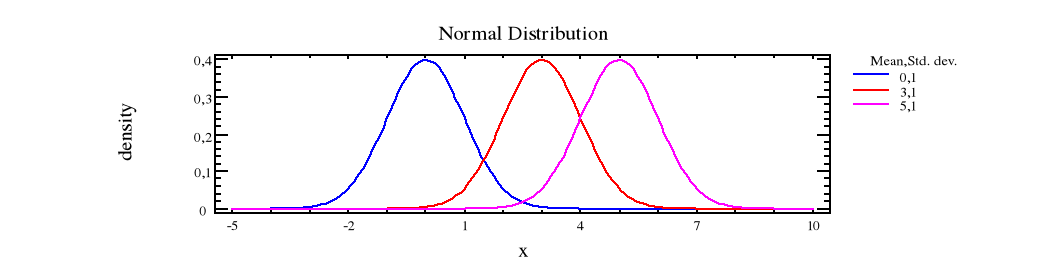
jak widać z wykresu wartość parametru m decyduje o położeniu względem osi x

ad 2b

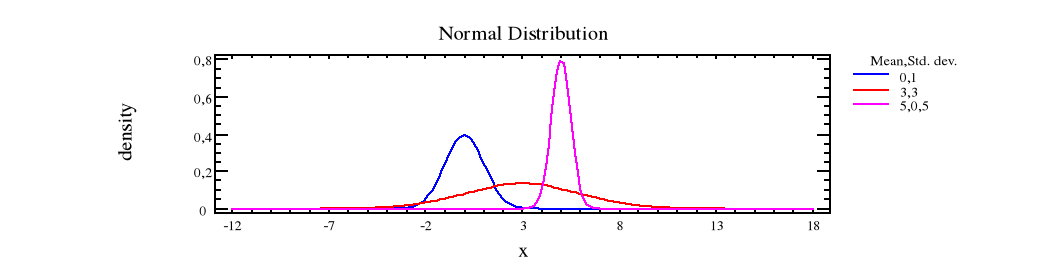
natomiast własności 2 i 3 wskazują, że od wartości σ zależy smukłość krzywej, widzimy wraz ze zwiększaniem odchylenia standardowego rozkład staje się bardziej spłaszczony, oznacza to że częściej występują wartości znacznie odbiegające od średniej

Bardzo dużo metod statystycznych (np. analiza wariancji) zakłada, że zmienna lub zmienne mają rozkład normalny, dlatego też jest to najważniejszy typowy rozkład zmiennych ciągłych.

Wnioskowanie statystyczne:

A: Estymacja - punktowa i przedziałowa

B: Weryfikacja hipotez - parametrycznych

Estymacja jest podstawowym działem wnioskowania statystycznego. Estymacja polega na szacowaniu wartości parametrów ewentualnie postaci rozkładu zmiennej losowej w populacji generalnej na podst rozkładu empirycznego dla próby.

Jeżeli szacuję się tylko wartości parametrów rozkładu populacji generalnej, mówimy o estymacji parametrycznej.

W estymacji punktowej- za ocenę wartości parametru przyjmuje się konkretną wartość otrzymaną na podstawie próby losowej.

W estymacji przedziałowej- szacuje się z wykorzystaniem odpowiednich reguł przedział liczbowy, który z określonym p-stwem pokryje wartość szacowanego parametru.

Estymatory parametrów teoretycznych z populacji generalnej na podst próby, tj estymatorem wartości średniej m (μ) jest średnia z próby (arytmetyczna), estymatorem wariancji jest wariancja z próby, odchylenia standardowego odchylenie standardowe z próby

Parametr	Estymator parametu	Estymator parametu
m (μ)
σ²
σ

Współczynniku zmienności

Polecenie 2

Wykonanie w programie Statgraphics wersja 4.1

1. Wykonaj zadania 1-5, w których wykonaj polecenie a)

1. Estymacja punktowa

Rozwiązanie:

1. Cecha X- zawartość tłuszczu (%) w mleku krów pewnej rasy

2. Założenia: cecha X ma w populacji rozkład normalny z nieznanymi parametrami, X~N(μ,σ²), gdzie μ,σ² są nieznane

3. Próba prosta n=10 elementowa; n<30 (próba mała)

4. Estymacja parametru μ, σ², σ, CV

-za ocene parametru m przyjmujemy średnią z próby (średnią arytmetyczną)

5. Obliczamy parametry próby

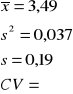
6. Interpretacja: uogólnienie wyników z próby losowej na populację generalną

Odp. Średnia (przeciętna) zawartość tłuszczu w mleku pewnej rasy krów wynosi m=3,49%

Wariancja zawartości tłuszczu w mleku pewnej rasy krów wynosi σ²=0,037

Odchylenie standardowe zawartości tłuszczu w mleku pewnej rasy krów wynosi σ=0,19, czyli zawartości tłuszczu w mleku tej rozpatrywanej rasy krów odchylają się od przeciętnej 3,49 średnio (+;-) 0,19%. Zawartość tłuszczu w mleku różniła się od przeciętnej równej 3,49% średnio (+;-) 0,2 %

Współczynnik zmienności CV=54,7%; zaobserwowany poziom zróżnicowania stanowił 55% przeciętnej zawartości tłuszczu w mleku

b) Estymacja przedziałowa

polega na szukaniu nie punktu oceny dla parametru populacyjnego m i σ tylko przedziału liczbowego, w którym m i σ zawiera się z określonym p-stwem.

Przedział ufności dla średniej μ (m) przy poziomie ufności 1- α

gdzie: n- liczebnośc próby, v=n-1 liczba stopni swobody, α- poziom istotności

Rozwiązanie:

1. Cecha X- zawartość tłuszczu (%) w mleku krów pewnej rasy

2. Założenia: cecha X ma w populacji rozkład normalny z nieznanymi parametrami, X~N(μ,σ²), gdzie μ,σ² są nieznane

3. Próba prosta n=10 elementowa; n<30 (próba mała)

4. Wyznaczamy ocenę przedziałową średniej zawartości tłuszczu w mleku w pewnej rasie krów μ przy poziomie ufności 1-α=0,95; 0,99 albo 95%, 99% przedział ufności dla średniej zawartości tłuszczu w mleku w pewnej rasie krów

5. Estymacja parametru μ, σ², σ,

6. Obliczamy parametry próby

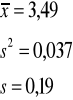
7. Podstawiamy do wzoru w.w

Odp. 95% przedział ufności dla średniej μ jest (3,35; 3,62)

Odp: Srednia μ є(3,35; 3,62) przy poziomie ufności P=0,95

Interpretacja: P-stwo, że średnia należy do tego przedziału wynosi 0,95 (95%)

Przedział ufności dla wariancji σ² przy poziomie ufności 1- α

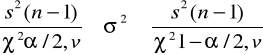
Przedział ufności dla odchylenia standardowego σ przy poziomie ufności 1- α

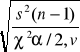
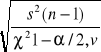
7. Podstawiamy do wzoru w.w

Odp. 95% przedział ufności dla odchylenia standardowego jest (0,13; 0,34)

Odp: Odchylenie standardowe σ є(0,13; 0,34) przy poziomie ufności P=0,95

Interpretacja: P-stwo, że odchylenie standardowe należy do tego przedziału wynosi 0,95 (95%)

---