Optyka falowa

1. Na czym polega zjawisko fotoelektryczne zewnętrzne?

2. W jaki sposób można spolaryzować światło? Co to jest kąt Brewstera?

3. Wyjaśnij budowę i zasadę działania lasera.

4. Podaj postulaty Bohra dotyczące budowy atomu wodoru.

5. Podaj teorię de Broglie'a.

6. Jak można wzbudzić atomy?

7. Podaj i opisz dowody na to, że światło wykazuje naturę falową.

8. Co stanie się z wiązką światła monochromatycznego przechodzącego przez siatkę dyfrakcyjną? Jakie można wysnuć wnioski z tego doświadczenia?

9. Długości fal świetlnych zawierają się w granicach od 3,8 *10^-7 m do 7,8 *10^-7 m. W jakim zakresie zawierają się energie fotonów świetlnych? c = 3 *10⁸ m/s, h = 6,63 *10^-34 J*s

10. Wiedząc, że energia atomu wodoru w stanie podstawowym równa się -13,6 eV oblicz długość kwantu światła emitowanego przez ten atom, gdy elektron zmienia orbitę z trzeciej (n = 3) na pierwszą (n = 1). 1 eV = 1,6 * 10^-19 J; (stała Rydberga R = 1,1 * 10⁷ 1/m)

11. Jak jest zbudowana i jak działa fotokomórka?

12. Na czym polega analiza widmowa? Jakie znasz rodzaje widm, jak one wyglądają i powstają?

13. Jaka powinna być maksymalnie praca wyjścia z metalu, aby zbudowana z niego fotokomórka mogła być czuła w całym obszarze widzialnym (λ w zakresie od 0,4 μm do 0,7 μm)?

14. Jaką długość fali należy przypisać cząstce o masie 1 mg, poruszającej się z prędkością 1 cm/s? c = 3 *10⁸ m/s, h = 6,63 *10^-34 J*s

16.

17. W atomie wodoru nieoznaczoność położenia elektronu jest równa promieniowi jego orbity w stanie podstawowym, czyli około 5,3*10^-11 m. Oblicz niepewność pomiaru wartości pędu w tym stanie.

18. Katoda fotokomórki oświetlana jest wiązką światła laserowego o długości fali 330 nm. Charakterystykę prądowo-napięciową tej fotokomórki przedstawiono poniżej na wykresie:

a. Korzystając z wykresu oblicz pracę wyjścia elektronów z tej fotokomórki.

b. Tę samą fotokomórkę oświetlamy światłem o innej długości fali. Zapisz, jaki warunek musi być spełniony, aby po przyłożeniu odpowiedniego napięcia przez fotokomórkę popłyną prąd?

c.

19. Wzbudzony atom wodoru emituje promieniowanie związane z przejściem elektronu z powłoki trzeciej na drugą. Oblicz energię wyemitowanego kwantu i długość fali uzyskanej linii widmowej. Zapisz, czy linia ta wypada w zakresie światła widzialnego, jeśli światło widzialne zawiera fale w przedziale od 380 nm do 760 nm. Energia stanu podstawowego atomu wodoru E = -13,6 eV.

20. Louis de Broglie przewidział, że cząstki elementarne wykazują własności falowe - cząstka o pędzie p jest falą o długości h/p. Oblicz długość fali powolnego neutronu o energii kinetycznej E = 1,6*10^-21 J. (Pomiń efekty relatywistyczne).

21. Na powierzchnię metalu, dla którego praca wyjścia wynosi W = 1,8 eV, pada:

1. 500 fotonów o energii 2 eV każdy;

2. 1000 identycznych fotonów o energii 1,7 eV każdy.

Oblicz, ile elektronów zostanie wybitych w każdym z podanych przypadków oraz jaka będzie energia kinetyczna każdego z nich. Odpowiedź krótko uzasadnij.

22. Powstanie obrazów badanych próbek w mikroskopach elektronowych jest

1. wynikiem przekazywania energii kinetycznej elektronów atomom próbki;

2. dowodem na istnienie zjawisk optycznych jeszcze nie do końca wyjaśnionych;

3. potwierdzeniem istnienia fal materii (dualizm korpuskularno-falowy);

4. wynikiem przekształcenia się części elektronów na falę świetlną.

23. Zasada nieoznaczoności Heisenberga stwierdza, że

1. im dokładniej ustalimy wartość pędu cząstki, tym dokładniej znamy jej położenie;

2. im dokładniej ustalimy wartość pędu cząstki, tym mniej dokładnie znamy jej położenie;

3. im mniej dokładnie znamy wartość pędu cząstki, tym mniej dokładnie możemy ustalić jej położenie;

4. nie ma związku pomiędzy dokładnościami ustalenia pędu i położenia cząstki.

24. Światło emitowane przez laser pada na ciało doskonale czarne (pochłaniające 100% padającego na nie promieniowania). Oblicz liczbę fotonów w impulsie światła laserowego, jeżeli pochłonięta energia jest równa 0,5 J. W obliczeniach przyjmij, że długość fali świetlnej emitowanej przez laser w próżni jest równa 700 nm.

25.

26. Podczas odczytu za pomocą wiązki światła laserowego informacji zapisanych na płycie CD wykorzystywane jest zjawisko

1. polaryzacji,

2. odbicia,

3. załamania,

4. interferencji.

27. Dlaczego polaroid polaryzuje światło?

28. Na siatkę dyfrakcyjną, która ma 200 rys na 1 mm, pada prostopadle światło długości fali 600 nm. Jaki największy rząd widma może być obserwowany w tych warunkach?

29. Elektron ma energię kinetyczną równa 1 eV. Porównaj długości fali materii tego elektronu z długościami fal drugiego elektronu o energii kinetycznej 1 keV oraz neutronu o energii 1 keV.

30. Czy istnieje możliwość równoczesnego, bardzo dokładnego pomiaru prędkości i położenia cząstki obserwowanej pod mikroskopem? Odpowiedź uzasadnij.

31. Oblicz wartość prędkości elektronu będącego na pierwszej orbicie atomu wodoru. Jak zmianie się ta wartość w zależności od numeru orbity? Promień pierwszej orbity 0,53*10^-10 m, masa spoczynkowa elektronu 9,1*10^-31 kg.

32. Na płytkę metalową pada fala o długości 200 nm. Wybite z metalu elektrony mają wartości prędkości dochodzące do 1000 km/s. Oblicz pracę wyjścia elektronu z metalu.

33. Laser o mocy 0,1 W emituje w próżni monochromatyczną wiązkę światła o długości fali 633 nm i kołowym przekroju. Oszacuj liczbę fotonów zawartych w elemencie wiązki światła o długości jednego metra. Oblicz wartość siły, jaką wywierałaby ta wiązka laserowego padająca w próżni prostopadle na wypolerowana metalowa płytkę. Do obliczeń przyjmij, że w ciągu jednej sekundy na powierzchnię płytki 10¹⁷ fotonów. Załóż, że płytka odbija w całości padające na nią promieniowanie.

Oblicz też rząd widma, jaki można zaobserwować po skierowaniu tej wiązki prostopadle na siatkę dyfrakcyjną posiadającą 400 rys/mm.

34. Elektrony w mikroskopie elektronowym przyśpieszane napięciem 100 kV uzyskują prędkość równą 0,6c. Oblicz długość fali de Broglie'a tych elektronów. Potrzebne dane weź z tablic.

35. W pracowni fizycznej wykonano doświadczenie mające na celu badanie zjawiska fotoelektrycznego i doświadczalne wyznaczenie wartości stałej Plancka. W oparciu w wyniki pomiarów sporządzono poniższy wykres. Przedstawiono na nim zależność maksymalnej energii kinetycznej uwalnianych elektronów od częstotliwości światła padającego na fotokomórkę.

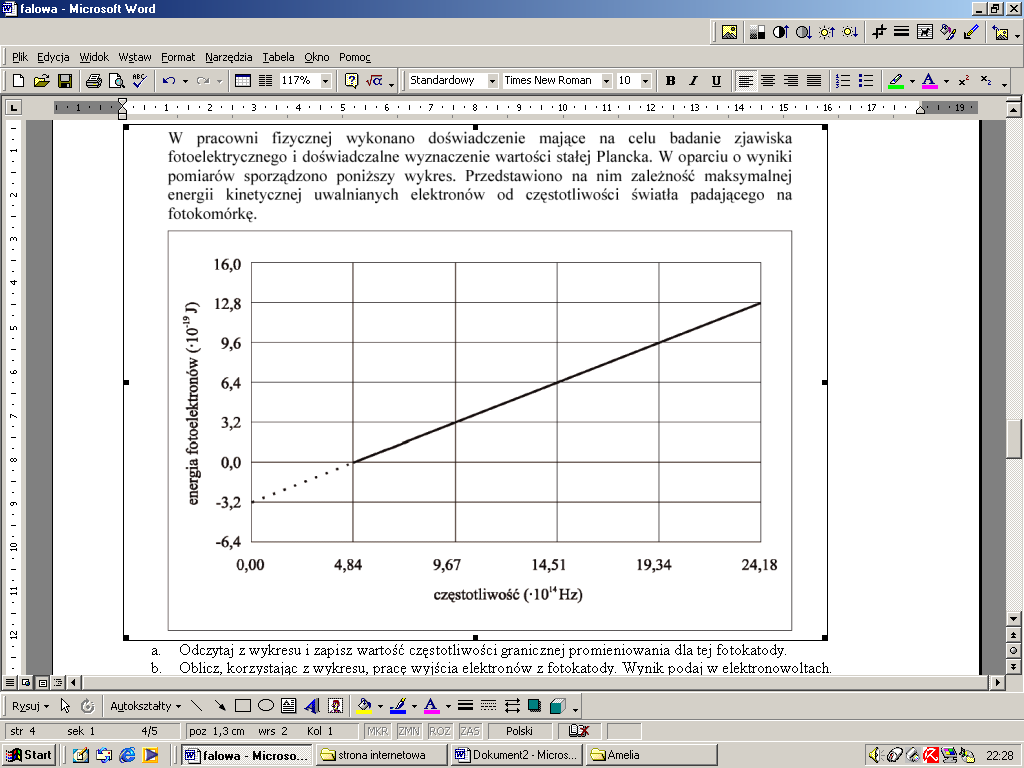
1. Odczytaj z wykresu i zapisz wartość częstotliwości granicznej promieniowania dla tej fotokatody.

2. Oblicz, korzystając z wykresu, pracę wyjścia elektronów z fotokatody. Wynik podaj w elektronowoltach.

3. Oblicz wartość stałej Plancka, wykorzystując tylko dane odczytane tylko z wykresu oraz zależność
   

36. Millikan zmierzył zależność napięcia hamowania od częstotliwości padającego światła dla dwóch fotokomórek, z których jedna miała fotokatodę z cezu, a druga z wolframu.

Wyniki jego pomiarów przedstawia wykres obok.

Jaką wartość stałej Plancka otrzymał Millikan, posługując się wartościami odczytanymi
z wykresu?

37. Światło przy odbiciu od powierzchni szkła ulega także polaryzacji liniowej. Całkowita polaryzacja liniowa zachodzi dla określonego kąta padania α_B. Przedstaw na rysunku warunek wystąpienia całkowitej polaryzacji (zaznacz kąt α_B) i wykaż, że bezwzględny współczynnik załamania szkła można obliczyć z zależności n = tg α_B.

38. Rysunek przedstawia schemat układu pomiarowego z fotokomórką, przy użyciu którego mierzono wartości napięcia hamowania. Napięciem hamowania nazywamy napięcie, przy którym nie płynie prąd w obwodzie fotokomórki, pomimo oświetlenia jej katody swiatłem powodującym przy wyższym napięciu przepływ prądu w obwodzie. Wartość działki elementarnej woltomierza ΔU wynosi 0,01 V.

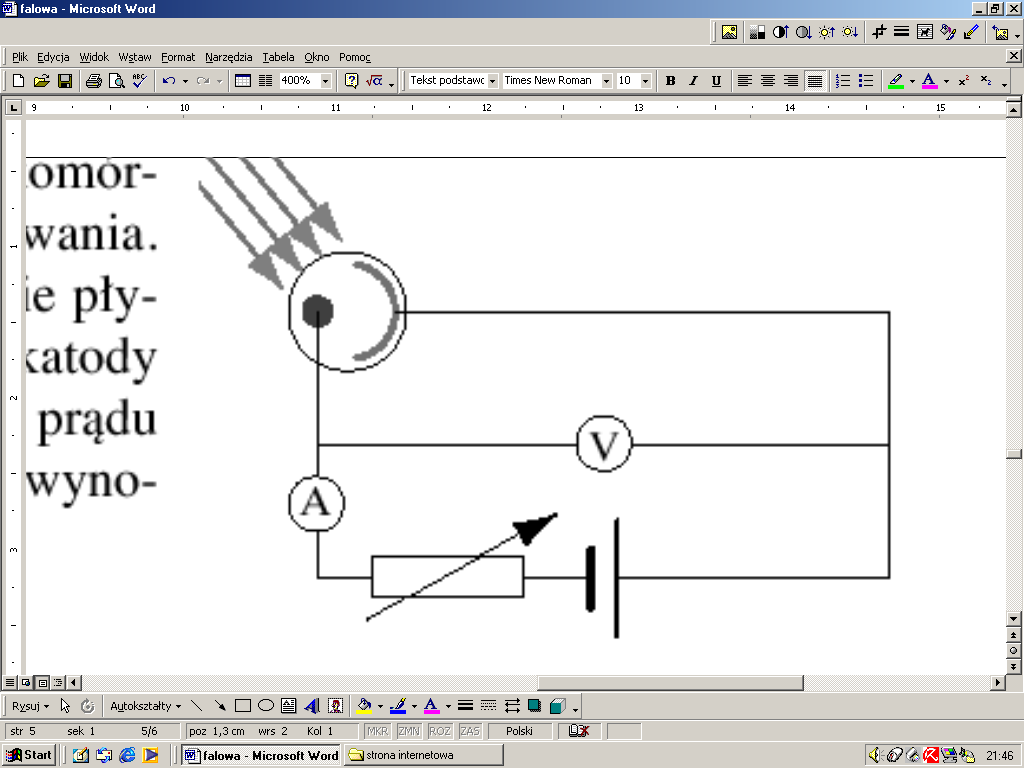
a. Narysuj przykładową charakterystykę prądowo-napięciową fotokomórki i zaznacz na niej napięcie hamowania U_h.

b. Oświetlając katodę fotokomórki światłem o różnych długościach fali, uzyskano wyniki przedstawione w pierwszym i czwartym wierszu poniższej tabeli. Oblicz i zapisz w pustych miejscach brakujące wartości.

λ(nm)	405	436	536	584
f*10^14 (Hz)
Uh (V)	1,15	0,93	0,42	0,24
eUh (eV)

c. Wartość iloczynu ładunku elektronu i napięcia hamowania jest równa maksymalnej energii kinetycznej fotoelektronów E_kmax. Sporządź wykres zależności wartości E_kmax od częstotliwości padającego światła na podstawie danych w tabeli. Zaznacz odcinki niepewności pomiarowej ΔE_kmax.

d. Katoda fotokomórki użytej w doświadczeniu jest wykonana z cezu, dla której wartość pracy wyjścia wynosi W = 1,97 eV. Oblicz, jaka co najmniej musi być częstotliwość światła padającego na katodę tej fotokomórki, aby zachodziło uwalnianie elektronów z powierzchni metalu.

39. Oblicz długość fali materii elektronu poruszającego się z prędkością o wartości u = 0,6c. Uwzględnij efekty relatywistyczne.

40. Aby wyrwać elektron z powierzchni cezu należy wykonać pracę wyjścia W = 1,6*10^-19 J. Oblicz energię kinetyczną i maksymalną prędkość wylatujących elektronów, jeżeli cez jest oświetlany światłem żółtym o długości fali λ = 589 nm.

41. Na siatkę dyfrakcyjną pada żółte światło o długości fali 550 nm. Na ekranie umieszczonym w pobliżu siatki widać prążek drugiego rzędu pod kątem 60⁰ w stosunku do obrazu centralnego. Oblicz stałą siatki. W opisanym przypadku nie można zobaczyć prążka trzeciego rzędu. Dlaczego?

42. Poniższa tabela przedstawia długości fal światła, które powstają przy przeskoku elektronu z orbity n na poziom podstawowy n = 1 (seria Lymana). Oblicz w eV (elektronowoltach) różnicę energii pomiędzy poziomem podstawowym a poziomem 4.

Numer początkowej orbity	Długość fali (nm)
2	121,6
3	102,6
4	97,0
5	94,9

43. Po lekcji o budowie i zasadzie działania fotokomórki nauczyciel fizyki polecił uczniom zaprojektować układ, który włączałby oświetlenie, kiedy zapada zmrok i wyłączał, kiedy zaczyna się dzień. Adam zaprojektował I układ, a Alek II układ. Poniższy rysunek przedstawia oba układy. Opis przy układzie I dotyczy także układu II.

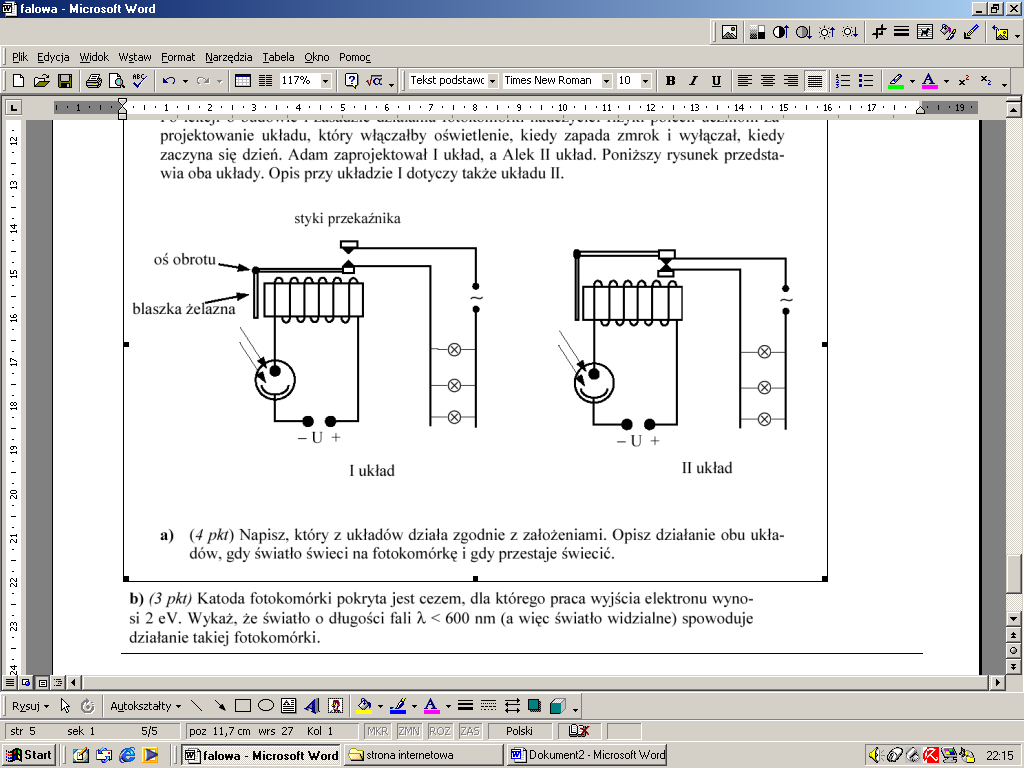
a. Napisz, który z układów działa zgodnie z założeniami. Opisz działanie obu układów, gdy światło świeci na fotokomórkę i gdy przestaje świecić.

b. Katoda fotokomórki pokryta jest cezem, dla którego praca wyjścia elektronu wynosi 2 eV. Wykaż, że światło o długości fali λ < 600 nm ( a więc światło widzialne) spowoduje działanie tej fotokomórki.

---