Zagadnienia do egzaminu z matematyki
Algebra liniowa
Podaj definicję iloczynu skalarnego wektorów
Iloczyn skalarny wektorów x i y jest liczbą określoną następująco:
Kiedy wektory są ortogonalne?
Układ m wektorów jest ortogonalny gdy wektory te są parami ortogonalne.
Podać definicję normy euklidesowej wektora x
Normą euklidesową wektora x nazywamy nieujemną liczbę:
Niech dana będzie przestrzeń liniowa
nad ciałem liczb rzeczywistych
wymiaru
w której określony jest standardowy iloczyn skalarny (nazwany euklidesowym). Przestrzeń afiniczną
nazywa się wówczas przestrzenią euklidesową wymiaru
Podać definicję kombinacji liniowej wektorów x1, ..., xm
Wektor
Kiedy wektory x1, ..., xm ∈ Rn nazywamy liniowo niezależnymi? Podaj przykład dwóch wektorów liniowo zależnych
Wektory
nazywamy liniowo niezależnymi, jeżeli ich kombinacja liniowa jest wektorem zerowym tylko wtedy, gdy wszystkie współczynniki
są równe zero.
Jeżeli wektory nie są liniowo niezależne, to mówimy, że są liniowo zależne.
Przykłady wektorów liniowo zależnych:
Podaj definicję macierzy.
Macierzą liczbową o n wierszach i m kolumnach nazywamy prostokątną tablicę zawierającą m-n liczb.
Tablicę taką zapisujemy w postaci
Jeśli elementy macierzy są liczbami rzeczywistymi to macierz nazywamy rzeczywistą.
Marcierz może zawierać inne elementy, np. funkcje - wtedy taką macierz nazywamy funkcyjną.
Podaj przykład macierzy trójkątnej dolnej.
Jaki jest warunek konieczny mnożenia macierzy?
Warunek konieczny:
Zasada mnożenia “wiersze przez kolumny”.
Mnożenie macierzy jest łączne ale nie przemienne. Jeśli AB istnieje to BA niekoniecznie, a jeśli nawet istnieją oba iloczyny to zazwyczaj nie są równe.
Zawsze można mnożyć przez siebie macierze kwadratowe tego samego stopnia.
Które z poniższych wzorów są prawdziwe (A, B, C - macierze)
A+(B+C)=(A+B)+C
A+B=B+A
A(BC)=(AB)C
AB=BA
A(B+C)=AB+AC
(A+B)C=AC+BC
(A+B)T= AT + BT (AB)T= BT * AT
Wymień działania elementarne na macierzach.
Wyróżnia się szereg działań na kolumnach i wierszach macierzy nazywanych powszechnie operacjami na macierzach.
Mnożenie wiersza przez niezerową stałą
Odejmowanie od wiersza innego wiersza pomnożonego przez stałą
Zamiana wierszy
Zamiana kolumn
Usuwanie zera z i-tej pozycji przekątnej macierzy
Metoda eliminacji Gaussa
Metoda eliminacji Gaussa-Jordana
Jak obliczyć wyznacznik macierzy stopnia n za pomocą rozwiniecia Laplace'a?
Minorem Mik elementy aik wyznacznika macierzy kwadratowej A stopnia n-1 która powstaje z macierzy A po opuszczeniu i-tego wiersza i k-tej kolumny.
Dopełnieniem algebraicznym Aik elementu aik wyznacznika nazywamy iloczyn.
Twierdzenie Laplace'a
Wyznacznik macierzy A stopnia n jest równy sumie iloczynów każdego elementu dowolnego wiersza (kolumny) i odpowiadającego temu elementowi dopełnieniu algebraicznego.
Aby obliczyć wyznacznik macierzy za pomocą rozwinięcia Laplace'a należy obliczyć dopełnienie algebraiczne wszystkich elementów oraz pomnożyć je przez odpowiadający element macierzy (ik). W tym celu najlepiej przeprowadzić eleiminację Gaussa na jednej z kolumn.
Co się stanie z wyznacznikiem macierzy A, jeżeli przestawimy w niej (zamienimy miejscami) dwa wiersze, a co - gdy przestawimy dwie kolumny?
Podczas przestawienia wiersza lub kolumny wyznacznik macierzy zmienia znak.
Co się stanie z wyznacznikiem macierzy A, jeżeli jeden z jej wierszy pomnożymy przez 7, a co - gdy jedną z jej kolumn podzielimy przez 2
Jeśli macierz B powstaje z macierzy A przez pomnożenie wszystkich elementów jednego wiesza lub kolumny przez C to.
Pomnożenie jednego z wierszy macierzy przez 7 (czyli stałą) spowoduje zmianę wyznacznika o 1/7. Zatem aby wyznacznik był prawidłowy należy przemnożyć go wcześniej przez tą stałą.
Analogiczną sytuację mamy przy podzieleniu wiersza / kolumny przez 2. W ów czas należy także podzielić wyznacznik przez tę liczbę.
Podać definicję dopełnienia algebraicznego elemnentu aij macierzy kwadratowej A.
Minorem Mik elementy aik wyznacznika macierzy kwadratowej A stopnia n-1 która powstaje z macierzy A po opuszczeniu i-tego wiersza i k-tej kolumny.
Dopełnieniem algebraicznym Aik elementu aik wyznacznika nazywamy iloczyn.
Podać definicję minora Mij.
Minorem Mik elementy aik wyznacznika macierzy kwadratowej A stopnia n-1 która powstaje z macierzy A po opuszczeniu i-tego wiersza i k-tej kolumny.
Podać definicję macierzy dołączonej do danej macierzy A.
Macierzą dołączoną AD macierzy kwadratowej a=[aik] nazywamy macierz transponowaną macierzy utworzonej z dopełnień algebraicznych elementów macierzy A tzn.
gdzie Aik jest dopełnieniem algebraicznym elementu aik
Ile wynosi wyznacznik macierzy o dwóch liniowo zależnych wierszach?
Wyznacznik macierzy o dwóch jednakowych wierszach jak i liniowo zależnych zawsze równy jest 0.
Jakie są własności macierzy nieosobliwej?
Definicja: Macierz kwadratową A dla której det A = 0 nazywamy macierzą nieosobliwą.
Twierdzenie: Macierz odwracalna jest macierzą nieosobliwą.
Podać własności macierzy odwrotnej.
Macierz B nazywana jest macierzą odwrotną do macierzy A jeśli
AB = BA = I
Gdzie I jest macierzą jednostkową. Macierz odwrotną oznaczamy A-1 Macierz A nazywa się macierzą odwracalną, jeśli istnieje macierz odwrotną do macierzy A.
Własności macierzy odwrotnej:
Jeżeli istnieje macierz odwrotna do macierzy A, to jest ona tylko jedna
Macierz odwrotna A-1 do macierzy kwadratowej A istnieje wtedy, gdy A jest nieosobliwa
(A-1)-1 = A
(AT)-1 = (A-1)T
Jeśli A i B są macierzami nieosobliwymi tego samego stopnia, to: (AB)-1 = B-1A-1
Czy wyznacznik ulega zmianie, gdy do elementów jednego wiersza dodać odpowiednie elementy innego wiersza pomnożone przez dowolną stałą?
Wyznacznik nie ulega zmienie, gdy do elementów jednej kolumny (wiersza) dodać odpowiednie elementy innej kolumny (wiersza) pomnożone przez dowolną stałą.
Czy wyznacznik ulega zmianie, gdy do elementów jednej kolumny dodać odpowiednie elementy innej kolumny pomnożone przez dowolną stałą?
Nie ulega zmianie
Jaki warunek musi spełniać macierz A, by istniała macierz odwrotna do niej? Podaj przykład macierzy, dla której nie istnieje macierz odwrotna.
Macierz B nazywamy macierzą odwrotną do macierzy A, jeśli AB=BA=1, gdzie 1 jest macierzą jednostkową. Macierz odwrotna oznaczamy A-1. Macierz A nazywa się macierzą odwrotna , jeśli istnieje macierz odwrotna do macierzy A.
Jeśli istnieje macierz odwrotna do macierzy a, to jest ona tylkop jedna.
Macierz odwrotna A-1 do macierzy kwadratowej A istnieje wtedy, gdy A jest nieosobliwa.
(A-1)-1=A
(AT)-1=(A-1)T
Jeśli A i B są macierzami nieosobliwymi tego samego stopnia to : (AB)-1=B-1A-1
Podać definicję rzędu macierzy.
Rząd macierzy A(rzA) o wymiarach m x n jest to maksymalna liczba niezależnych liniowo kolumn/wierszy.
Jest stopniem największej kwadratowej podmacierzy nieosobliwej zawartej w A.
Aby obliczyć rząd macierzy A należy zastosować do tej macierzy metode eliminacji Gaussa-Jordana. Sprowadzając ja do jednej z postaci bazowych. Wymiar wyróżnionej tam macierzy jednostkowej równy jest rzA.
Jakie operacje na wierszach macierzy (operacje elementarne) nie zmieniają rzędu macierzy?
1 Do dowolnego wiersza(kolumny) dodamy inny wiersz(kolumne) pomnożoną przez liczbę rożną od zera
2 Dowolny wiersz(kolumne) pomnożymy lub podzielimy przez liczbę różną od zera
Ile rozwiązań może mieć układ m równań liniowych o n niewiadomych?
nieskonczenie wiele
Podać warunek konieczny i dostateczny rozwiązalności układu równań.
Warunkiem koniecznym i dostatecznym rozwiozalności układu równań liniowych jest spełnienie równania rzA=rzAI=K
Jeśli ponadto K=m(liczb niewiadomych) to układ jest oznaczony, w przeciwnykm wypadku jest nieoznaczony i rozwiązania stanowią zbiór zależny od(n-k) parametru u.
f'(x)=0 jest warunkiem koniecznym na to aby funkcja f(x)różniczkowalna miała w tym punkcie ekstremum warunek konieczny
warunek dostateczny funkcja f'(x)=0 ponadto f'(x) zmienia znak z ujemnego na dodatni gdy malejac przechodzi przez punkt x0 to ma w tym punkcie minimum
f'(x) zmienia znak z dodatniego na ujemny gdy rosnac przechodzi przez punkt x0 to ma w tym punkcie max
Kiedy układ n równań o n niewiadomych będzie
Oznaczony- 1 rozwiązanie
Nieoznaczony- więcej niż 1 rozwiązanie
Sprzeczny- brak rozwiązania
Kiedy układ równań liniowych jest układem Cramera?
Układ równań liniowych spełniającym warunek rz(A)=n=m nazywamy Cramera. W zapisie macierzowym ma on postać AX=B. Macierz współczynników A jest macierzą nieosobliwą, rzn det A(rożny ) od 0
Rachunek różniczkowy funkcji jednej i wielu zmiennych
Co rozumiemy przez granicę funkcji f(x) w punkcie x0?
Granica fukcji w pkt wg heinego:
Liczbę g nazywa się granicą funkcji f(x) w pkt x0 jeśli dla każdego ciągu {xn} o wymiarach xn należacego do S i zbieżnego x0, ciąg wartości f{f(xn)} jest zbieżny do g
Granica funkcji w pkt wg Cauchy'ego
Liczbę g nazywa się granicą funkcji f(x) w pkt x0 wtedy i tylko wtedy jeśli dla każdej liczby >0 istnieje taka liczba >0, a dla każdego x spelniającego warunek 0 < Ix-x0I<0
Liczbę g nazywamy granicą funkcji f w punkcie x0, jeżeli dla każdego ciągu (xn) o wyrazach xn ∈ S, zbieżego do x0, ciąg (f(xn)) wartości funkcji jest zbieżny do g.
Zdanie: "liczba g jest granicą funkcji f w punkcie x0" zapisujemy
limx→x0f(x)=g lub f(x)→x→x0g
Podać definicję ciągłości funkcji w punkcie.
Funkcje f(x) nazywa się ciągłą w pkt x0wtedy i tylko wtedy gdy
limx-o f(x)=f(x1)
Na to aby funkcja f(x) była ciągła w pkt x0 potrzeba aby funkcja:
Była okreslona w pkt +0
Miała równa granicę jednostronna
Miała wartość w pkt x0 równą granicom jednostronnych
Kiedy mówimy, że funkcja f przekształca zbiór X na zbiór Y?
Funkcja przekształca zbiór X na zbiór Y, gdy w zbiorze X została określona funkcja, której wartościami są elementy zbioru Y, czyli gdy zachodzi równość f(X)=Y
Kiedy funckja f jest różnowartościowa? Podaj przykład funkcji nieróżnowartościowej.
Funkcja różnowartościowa to taka, której każdy element przeciwdziedziny przyjmowany jest co najwyżej raz.
Przykład funkcji nieróżnowartościowej: taka funkcja w której argumentowi a i b z pierwszego zbioru odpowiada ta sama wartość ze zbioru drugiego.
Podać definicję funkcji malejącej. Podaj przykład funkcji malejącej.
Funkcja malejąca-to taka, której wartości maleją w miarę wzrastania argumentu.
tzn. x1 < x2 wynika f(x1) > f(x2)
Podać definicję funkcji rosnącej. Podaj przykład funkcji rosnacej.
Funkcja rosnąca-funkcja, której wartości rosną w miarę wzrastania argumentu
x1 < x2 wynika f(x1) < f(x2)
Podać definicję funkcji okresowej. Podaj przykład funkcji okresowej.
Funkcja y=f(x) jest funkcją okresową o okresie f, jeśli istnieje taka liczba f różnej od 0, która dodana do dowolnej dopuszczalnej wartości argumentu nie zmienia wartości funkcji tzn. f(x=f)=f(x'). Najmniejszą liczbę dodatnią o f samej własności (jeżeli istnieje nazywamy okresem podstawowym, zasadniczym funkcji.
Przykładem funkcji okresowych jest f trygonometryczna oraz f stała. Funkcja y=sinx jest okresowa o okresie podstawowym 2 pi.
Podać definicję funkcji parzystej. Podaj przykład funkcji parzystej.
Funkcje nazywamy funkcją parzysta jeśli dla każdego x należącego do dziedziny f=-x również należy do dziedziny f(-x)=f(x)
Funkcja f jest parzysta wtedy i tylko wtedy gdy zbiór D f jest symetryczny względem zera oraz oś 0Y jest osią symetrii wykreu tej fukcji
Podać definicję funkcji nieparzystej. Podaj przykład funkcji nieparzystej.
Funkcje nazywamy funkcja nieparzysta jeśli dla każdego x należącego do dziedziny funkcji -x również należy do dziedziny oraz
f(-x)=-f(x)
funkcja jest nieparzysta wtedy i tylko wtedy gdy zbiór D= jest symetryczny względem zera oraz punkt 0=(0,0) jest środkiem symetrii wykresu tej funkcji.
Przykład:f(x)=1/x Df=R/(0)
F(-x)=-1/x=-f(x)
Naszkicuj wykres funkcji y=sinx oraz podaj jej własności.
F: R-R
X1<X2 wtedy i tylko wtedy gdy f(x1)<f(x2)
F jest rosnąca dla x należace go (- nieskonczonośc, x1) oraz x należącego do(x2,+ nieskończoność)
Funkcja jest malejąca dla x należącego do( x1,x2)
F jest okresowa gdy f9x+f)=f(x) jeśli cyklicznie się powtarza
Naszkicuj wykres funkcji y=cosx oraz podaj jej własności.
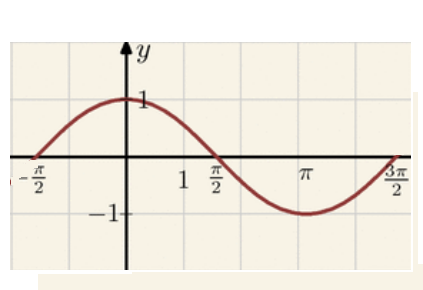
Podaj definicję funkcji odwrotnej. Podaj przykład funkcji wzajemnie odwrotnych.
Podaj przykład dowolnej funkcji cyklometrycznej (kołowej) oraz naszkicuj jej wykres.
Jakie warunki powinna spełniać funkcja f(x) aby posiadała funkcję odwrotną?
Podać definicję ilorazu różnicowego.
Podać geometryczną interpretację ilorazu różnicowego funkcji f(x) w punkcie x0.
Co to jest pochodna funkcji f(x) w punkcie x0?
Jak obliczyć pochodną sumy, różnicy, iloczynu i ilorazu funkcji f(x) oraz g(x)?
Podać geometryczną interpretację pochodnej funkcji f(x) w punkcie x0.
Jak wyznaczyć przedziały monotoniczności funkcji stosując jej pierwsza pochodną?
Podajć definicję minimum (maksimum) lokalnego funkcji.
Sformułuj warunek konieczny istnienia ekstremum funkcji.
Sformułuj warunek wystarczający istnienia ekstremum funkcji związany ze znakiem pierwszej pochodnej.
Podaj definicję funkcji wklęsłej. Jaki znak przyjmuje wtedy druga pochodna funkcji?
Podaj definicję funkcji wypukłej. Jaki znak przyjmuje wtedy druga pochodna funkcji?
Kiedy funkcja f(x) może (ale nie musi) mieć punkt przegięcia w punkcie x0 (warunek konieczny istnienia punktu przegięcia).
Podaj regułę de l'Hospitala.
Regułę l'Hospitala wykorzystuje się do liczenia granic wyrażeń nieoznaczonych. Do jej stosowania wymagane jest sprawne liczenie pochodnych.
Załóżmy, że funkcje f(x) oraz g(x) są określone w otoczeniu punktu a.
Wówczas jeżeli:
lub
to:
Powyższa równość zachodzi dodatkowo pod warunkiem, że granica po prawej stronie istnieje.
Punkt a może być konkretna liczbą, albo +∞ lub -∞.
Podaj definicję gradientu dla funkcji trzech zmiennych. - zdjęcie
Podaj definicję hesjanu dla funkcji trzech zmiennych.
Hesjan - kwadratowa macierz drugich pochodnych cząstkowych funkcji. Inaczej macierz Hessego
Jaka jest wartość gradientu funkcji wielu zmiennych w punkcie P, w którym istnieje ekstremum lokalne funkcji?
Funkcja f ma w punkcie (x0, y0) maksimum lokalne własciwe,
gdy f(x, y) < f(x0, y0).
Funkcja f ma w punkcie (x0, y0) minimum lokalne własciwe,
gdy f(x, y) > f(x0, y0).
Podać twierdzenie o istnieniu ekstremum lokalnego funkcji dwóch zmiennych.
Gradient w funkcji wielu zmiennych w punkcie P, w którym istnieje ekstremum lokalne funkcji jest wektorem zerowym.
Rachunek calkowy funkcji jednej zmiennej
Kiedy mówimy, że funkcja F(x) jest funkcją pierwotną funkcji f(x)?
Funkcją pierwotną danej funkcji f(x) nazywa się funkcję różniczkowalną F(x) taką, że F'(x)=f(x). Funkcja ma postać F(x)+C
Podać definicję całki nieoznaczonej.
Zbiór wszystkich funkcji pierwotnych względem danej funkcji f(x). Oznacza się symbolem: ∫ f(x)dx
Podać postać formuły całkowania przez części.
∫ udv=uv-∫vdu
przy użyciu symboliki różniczek:
du=u'(x)dx
dv=v'(x)dx
Podać geometryczną interpretację całki oznaczonej.
Wyznaczyć całki sprowadzając je do funkcji elementarnych a następnie stosując wzory całkowe:
Obliczyć całki metodą podstawiania:
Obliczyć całki metodą całkowania przez części:
Obliczyć całki z funkcji wymiernych:
Oblicz pole powierzchni ograniczonej wykresami
i
Oblicz pole powierzchni ograniczonej wykresami
,
i prostą
Oblicz pole ograniczone liniami: y2 = x3, y=8, x=0.
Wyszukiwarka
Podobne podstrony:
T 3[1] METODY DIAGNOZOWANIA I ROZWIAZYWANIA PROBLEMOW
Rozwiązywanie układów równań
ROZWIĄZYWANIE PROBLEMÓW
WYKŁAD 2 prawa obwodowe i rozwiązywanie obwodów 2003
Rozwiazywanie problemów
Rozwiązania instytucjonalne w zakresie realizacji i kontroli praw pacjenta
rozwiazywanie zadan tekstowych wb
zadania i rozwiazania z przekrojów 2
Rehabilitacja jako pomoc w rozwiązywaniu problemów życiowych niepełnosprawnych
Przegląd rozwiązań konstrukcyjnych wtryskarek (ENG)
Rozwiązywanie układów równań metodą wyznaczników
,projektowanie materiałów inżynierskich, zadania i rozwiązania Umocnienie roztworowe
Coaching mentoring i zarzadzanie Jak rozwiazywac problemy i budowac zespol
matematyka rozwiazania Nieznany
3 14 ukladanie i rozwiazywanie Nieznany
więcej podobnych podstron