3. ZBIEŻNE UKŁADY SIŁ

Sposób geometryczny wyznaczania wypadkowej - polega na zbudowaniu wieloboku sił, w którym wektory sił odkłada się równolegle do ich linii działania (jako wektory swobodne)

Płaski układ sił zbieżnych:

Płaski układ sił zbieżnych P₁, P₂ ,P₃, ... , P_n przyłożonych do punktu O można zastąpić siłą wypadkową P równą sumie geometrycznej tych sił i przyłożoną również w punkcie O.

Płaski układ sił zbieżnych:

Sposób geometryczny wyznaczania wypadkowej polega na zbudowaniu wieloboku sił, w którym wektory sił odkłada się równolegle do ich linii działania (jako wektory swobodne).

Z dowolnego punktu odkłada się wektor P, z jego końca wektor P₁, z końca wektora P­₁ wektor P₂ i tak kolejno wektory, aż do P_n. Wektor P poprowadzony od początku wektora P do końca wektora P_n jest sumą geometryczną wektorów P₁,P₂,P₃,...,P_n.

Płaski układ sił zbieżnych P₁,P₂,P₃,...,P_n przyłożonych do punktu O można zastąpić wypadkową P, równą sumie geometrycznej tych sił i przyłożoną również w punkcie O.

Wypadkowa płaskiego układu sił zbieżnych jest wektorem posuwnym, ponieważ ma określoną linię działania, podczas gdy suma geometryczna jest wektorem swobodnym.

W sposobie analitycznym wyznaczenia wypadkowej wykorzystuje się twierdzenie o rzucie sumy wektorów.

Twierdzenie o rzucie sumy wektorów:

Rzut sumy geometrycznej wektorów i na dowolną oś równy jest sumie rzutów tych wektorów na tę samą oś.

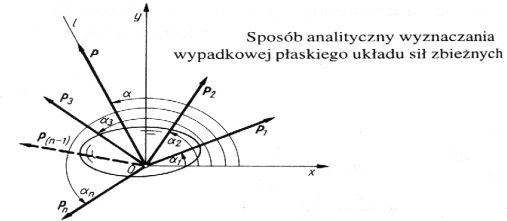
• układ dwóch wzajemnie prostopadłych osi Oxy,

• kąty nachylenia sił P₁ P₂, P₃,, P_n do osi x, oznaczono odpowiednio przez ₁, _2, ₃,. . _n

• wypadkowa sił działa wzdłuż prostej I przechodzącej przez punkt O i nachylonej do osi x pod kątem 

• wartość wypadkowej P i kąta  nie jest znana dlatego należy je wyznaczyć

Wyznaczenie wypadkowej P i kąta ၡ

- wyznaczenie składowych P_x i P_y

- określenie wartości liczbowych wypadkowej P i kąta a

Przestrzenny układ sił zbieżnych:

Przestrzenny układ sił zbieżnych P₁, P₂,..., P_n przyłożonych do jednego punktu O można zastąpić jedną siłą wypadkową P przyłożoną w tymże punkcie i równą sumie geometrycznej tych sił.

Wypadkowa dowolnej liczby n sił przyłożonych do jednego punktu:

Sposób geometryczny wyznaczania wypadkowej

Zastosowanie zasady równoległoboku

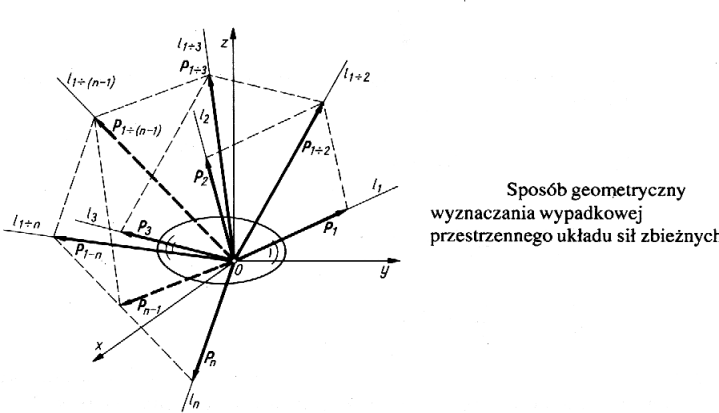
Sposób analityczny wyznaczenia wypadkowej

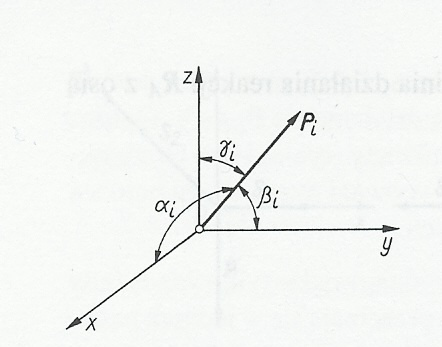
Aby wyznaczyć wypadkową układu sił P1, P2 ,....,Pn, których linie działania przechodzą przez punkt 0, przyjmuje się prostokątny układ osi Oxyz.

Oznaczając kąty nachylenia sił do osi x, y, z przez: α_i, β_i, γ_i, (i =1,2,..,n), oblicza się wartości algebraiczne rzutów wypadkowej P sił P_i, na odpowiednie osie układu

Obliczenie wartości składowych

Określenie wartości liczbowej (modułu) wypadkowej P oraz jej cosinusów kierunkowych:

• Linia działania wypadkowej przechodzi przez punkt 0, przez który przechodzą linie działania sił P.

• We wzorach α, β, γ oznaczają kąty, które wypadkowa P tworzy z osiami współrzędnych.

• Cosinusy kierunkowe spełniają zależność: cos²α + cos²β + cos²γ = 1

Równowaga płaskiego układu sił zbieżnych

• W szczególnym przypadku suma geometryczna płaskiego układu sił zbieżnych może być równa zeru.

• Wielobok zbudowany z tych sił jest wielobokiem zamkniętym a układ jego jest w równowadze.

Warunki równowagi płaskiego układu sił zbieżnych

1. Aby układ sił zbieżnych P₁, P₂, ... , P_n działających w jednej płaszczyźnie znajdował się w równowadze, wielobok utworzony ze wszystkich sił tego układu musi być zamknięty (warunek geometryczny).

Powyższemu warunkowi odpowiada następujące równanie wektorowe:

P₁ + P₂ + ... + P_n =

2. Aby siły zbieżne leżące w jednej płaszczyźnie były w równowadze, sumy rzutów tych sił na osie układu współrzędnych muszą być równe zeru (warunek analityczny).

Równania równowagi sił zbieżnych działających w jednej płaszczyźnie są następujące:

Rozwiązywanie zagadnień równowagi płaskiego układu sił zbieżnych

Dla układu sił zbieżnych o określonych liniach działania, należy dysponować danymi liczbowymi

(n- 2) sił. Wartości liczbowe dwóch niewiadomych sił można wyznaczyć z warunku równowagi. Zakłada się, że na bryłę działają trzy nierównoległe siły P₁ P₂ i P₃ (rys. a), będące w równowadze.

Równowaga trzech sił nierównoległych

Wypadkowa dwóch z tych sił (np. P₁ i P₂ czyli P_1,2) musi się równoważyć z siłą trzecią P₃, a więc siły P_1,2 i P₃ muszą być równe co do wartości liczbowych, przeciwne co do kierunku i muszą działać wzdłuż jednej prostej. Stąd wynika, że linia działania siły P₃ musi przechodzić także przez punkt 0, w którym przecinają się linie działania sił P₁ i P₂ . Oprócz tego, wielobok (trójkąt) sił P₁ ,P₂ i P₃ musi być zamknięty (rys. b).

Równowaga przestrzennego układu sił zbieżnych:

Warunek równowagi w postaci wektorowej

19

---