|
Wydział: FTiMK |
Imie i Nazwisko: Marcin Wiśniowski |
Nr. Zepołu 8 |
Ocena Ostateczna |
|
Grupa: Trzecia |
Tytół ćwiczenia: Wyznaczanie współczynnika lepkości dynamicznej cieczy |
Nr. Cwiczenia 7 |
Data Wykonania: 30.11.2001 |
Wprowadzenie
Lepkość - tarcie wewnętrzne, to właściwość ciał stałych, cieczy, ciekłych kryształów, gazów lub plazmy. Wynika z oddziaływań występujących przy wzajemnym przesuwaniu się elementów tego samego ciała. Oddziaływania te charakteryzujemy wprowadzając wielkości nazywane współczynnikami lepkości. Miarą tych oddziaływań są siły lepkości. W naszym ćwiczeniu zajmiemy się wyznaczeniem współczynnika lepkości dynamicznej cieczy.
Rozważmy warstwę cieczy o grubości Δl. Doświadczenie wskazuje, że przesunięcie ze stałą prędkością, równoległą do powierzchni cieczy, cienkiej płytki, doskonale zwilżanej, o polu powierzchni S (rozmiary liniowe płytki są większe od grubości warstwy), wymaga przyłożenia stycznej do płytki stałej siły F, która równoważy siłę lepkości FR. Siła lepkości istnieje między warstewką przylegającą do płytki i warstewką następną oraz między każdą sąsiednią parą warstewek. Poszczególne warstewki cieczy przesuwają się (ślizgają się) równolegle względem siebie, przy czym rozkład prędkości w kierunku osi x.
Doświadczalnie stwierdzono, że dla większości cieczy (nazywanych cieczami niutonowskimi) wartość siły oporu lepkiego jest proporcjonalna do pola powierzchni S i wartości gradiętu prędkości dv/dt
![]()
Współczynnikiem lepkości dynamicznej nazywamy współczynnik proporcjonalności η. Jego wymiarem jest: N-s/m2 = Pa∙s.
Siła ta uwarunkowana jest dwoma czynnikami: istnieniem sił spójności (w gazie nie występują) oraz ruchem termicznym cząsteczek, który występuje również między warstewkami cieczy o różnych prędkościach. Przechodzenie cząsteczek między warstewkami nie zmienia charakteru ruchu. Cząsteczki z warstwy o prędkości większej przechodzą do warstwy o prędkości mniejszej, przyspieszając ją. Średnio taka sama liczba cząsteczek przechodzi z warstwy o prędkości mniejszej do warstwy o prędkości większej, spowalniając ją. W miarę wzrostu temperatury siły spójności maleją. Wzrasta liczba przemieszczających się cząsteczek. Rezultatem tego jest zmniejszanie się siły oporu - przy ustalonym gradiencie prędkości i ustalonym S, siła lepkości maleje. Stąd w cieczach ze wzrostem temperatury współczynnik lepkości maleje, w przeciwieństwie do gazów, dla których obserwujemy wzrost współczynnika lepkości wraz z temperaturą.
Podsumowując, możemy stwierdzić, że współczynnik lepkości cieczy zależy od:
rodzaju cieczy, ponieważ od rodzaju cieczy zależą siły międzycząsteczkowe,
temperatury - maleje ze wzrostem ruchu termicznego cząsteczek.
Rozważania ograniczamy do przepływów laminarnych. W przepływach laminarnych ciecz płynie równoległymi warstwami z różnymi prędkościami, w odróżnieniu od przepływu burzliwego, w którym wektor prędkości elementów cieczy zmienia się chaotycznie.
Charakter przepływu (laminaray czy turbulentny) zależy od wartości bezwymiarowej wielkości Re zwanej liczbą Reynoldsa:
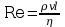
Metoda pomiaru
Wyznaczanie współczynnika lepkości dynamicznej η na podstawie prawa Stokesa
P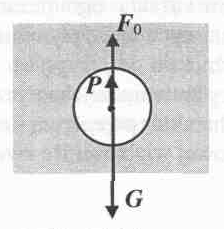 rzyjmijmy,
że w cieczy lepkiej, dla której Re «1, spada z niewielką
prędkością
v
kulka.
Spadająca kulka pociąga za sobą, z powodu istnienia sił
międzycząsteczkowych,
sąsiadujące z kulką warstwy cieczy. Układ warstw cieczy
ślizgających
się po sobie posiada różne prędkości. Kulka razem z warstewką
cieczy
do niej przylegającą doznaje działania siły oporu lepkiego F0.
Oprócz
siły
oporu F0
na
spadającą kulkę działają: siła ciężkości G oraz siła wyporu
P,
dana
prawem Archimedesa.
rzyjmijmy,
że w cieczy lepkiej, dla której Re «1, spada z niewielką
prędkością
v
kulka.
Spadająca kulka pociąga za sobą, z powodu istnienia sił
międzycząsteczkowych,
sąsiadujące z kulką warstwy cieczy. Układ warstw cieczy
ślizgających
się po sobie posiada różne prędkości. Kulka razem z warstewką
cieczy
do niej przylegającą doznaje działania siły oporu lepkiego F0.
Oprócz
siły
oporu F0
na
spadającą kulkę działają: siła ciężkości G oraz siła wyporu
P,
dana
prawem Archimedesa.
Wartość siły oporu F0 zależy od wielkości i kształtu poruszającego się ciała, od prędkości v ciała oraz od rodzaju cieczy, w której ciało porusza się. Dla kulki o promieniu r, jest ona określona prawem Stokesa:
F0 = 6πηfv
Można wykazać, że po pewnym czasie ustali się ruch jednostajny kulki. Zgodnie z I zasadą dynamiki Newtona mamy:
G + P + F0 = 0
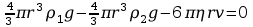
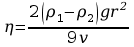
Liczba Reynoldsa Re dla kulki o promieniu r poruszającej się w cieczy określona jest wzorem:
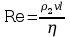
Wyznaczanie współczynnika lepkości dynamicznej η na podstawie prawa Hagena-Poiseuille'a
S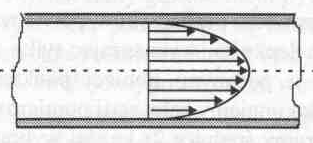 iły
oporu lepkiego występują również przy przepływie cieczy przez
rury czy kapilary. W rurkach przy przepływie laminarnym, do
wystąpienia którego
potrzebna jest stała różnica ciśnień Δp,
ustala się gradient prędkości. Największą
prędkość posiada warstewka cieczy poruszająca się wzdłuż osi
rurki przy czym
w miarę oddalania się
od osi w kierunku
ścianek rurki prędkość warstewek
maleje do zera.
iły
oporu lepkiego występują również przy przepływie cieczy przez
rury czy kapilary. W rurkach przy przepływie laminarnym, do
wystąpienia którego
potrzebna jest stała różnica ciśnień Δp,
ustala się gradient prędkości. Największą
prędkość posiada warstewka cieczy poruszająca się wzdłuż osi
rurki przy czym
w miarę oddalania się
od osi w kierunku
ścianek rurki prędkość warstewek
maleje do zera.
Tego typu przepływ opisuje ilościowo prawo Hagena-Poiseuille'a Podaje ono wzór na objętość V cieczy (lub gazu) o lepkości dynamicznej η, przepływającej w czasie τ przez kapilarę o promieniu R i długości l, na której końcach panuje stała różnica ciśnień p2–p1.
![]()
Na podstawie prawa Hagena-Poiseuille'a wyznaczamy zwykle względny współczynnik lepkości, tzn. stosunek współczynnika lepkości η danej cieczy do współczynnika lepkości ηw wody destylowanej pozostających w tej samej temperaturze. W tym celu stosuje się wiskozymetry z kapilarą pionową (Arrheniu-sa, Ostwalda, Englera itp.). Do wymienionych wiskozymetrów należy również wiskozymetr Ubbelohde.
Tabele pomiarowe i obliczenia.
|
Lp |
h1 |
h2 |
h3 |
h2 – h1 |
h3 – h1 |
ρw |
t |
ρ2 |
|
1 |
38,0 |
42,7 |
12,0 |
4,7 |
–26 |
0,999·103 |
22 |
0,846·103 |
|
Kulka 1 |
|||||||||
|
Lp |
2r [mm] |
s1 [cm] |
s2 [cm] |
l [cm] |
τ [s] |
2R [cm] |
ρ1 [kg·m-3] |
η [Nsm-2] |
η [Nsm-2] |
|
1 |
2,48 |
25,4 |
9 |
16,4 |
40,2 |
8,5 |
1,060 |
0,1796 |
0,1670 |
|
2 |
2,48 |
25,4 |
9 |
16,4 |
41,2 |
8,5 |
1,060 |
0,1796 |
0,1670 |
|
3 |
2,48 |
25,4 |
9 |
16,4 |
41,4 |
8,5 |
1,060 |
0,1796 |
0,1670 |
|
4 |
2,48 |
25,4 |
9 |
16,4 |
40,8 |
8,5 |
1,060 |
0,1796 |
0,1670 |
|
5 |
2,48 |
25,4 |
9 |
16,4 |
41,0 |
8,5 |
1,060 |
0,1796 |
0,1670 |
|
6 |
2,48 |
25,4 |
9 |
16,4 |
40,4 |
8,5 |
1,060 |
0,1796 |
0,1670 |
|
7 |
2,48 |
25,4 |
9 |
16,4 |
41,2 |
8,5 |
1,060 |
0,1796 |
0,1670 |
|
8 |
2,48 |
25,4 |
9 |
16,4 |
40,8 |
8,5 |
1,060 |
0,1796 |
0,1670 |
|
9 |
2,48 |
25,4 |
9 |
16,4 |
40,6 |
8,5 |
1,060 |
0,1796 |
0,1670 |
|
10 |
2,48 |
25,4 |
9 |
16,4 |
41,2 |
8,5 |
1,060 |
0,1796 |
0,1670 |
|
Kulka 2 |
|||||||||
|
Lp |
2r [mm] |
s1 [cm] |
s2 [cm] |
l [cm] |
τ [s] |
2R [cm] |
ρ1 [kg·m-3] |
η [Nsm-2] |
η [Nsm-2] |
|
1 |
2,27 |
25,4 |
9 |
16,4 |
48,8 |
8,5 |
1,060 |
0,1731 |
0,1637 |
|
2 |
2,27 |
25,4 |
9 |
16,4 |
48,6 |
8,5 |
1,060 |
0,1731 |
0,1637 |
|
3 |
2,27 |
25,4 |
9 |
16,4 |
47,2 |
8,5 |
1,060 |
0,1731 |
0,1637 |
|
4 |
2,27 |
25,4 |
9 |
16,4 |
47,8 |
8,5 |
1,060 |
0,1731 |
0,1637 |
|
5 |
2,27 |
25,4 |
9 |
16,4 |
48,2 |
8,5 |
1,060 |
0,1731 |
0,1637 |
|
6 |
2,27 |
25,4 |
9 |
16,4 |
48,6 |
8,5 |
1,060 |
0,1731 |
0,1637 |
|
7 |
2,27 |
25,4 |
9 |
16,4 |
48,4 |
8,5 |
1,060 |
0,1731 |
0,1637 |
|
8 |
2,27 |
25,4 |
9 |
16,4 |
47,8 |
8,5 |
1,060 |
0,1731 |
0,1637 |
|
9 |
2,27 |
25,4 |
9 |
16,4 |
48,2 |
8,5 |
1,060 |
0,1731 |
0,1637 |
|
10 |
2,27 |
25,4 |
9 |
16,4 |
48,8 |
8,5 |
1,060 |
0,1731 |
0,1637 |
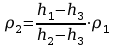
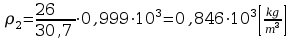
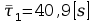
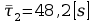
Obliczam teraz prędkość kulek uwzględniając poprawkę według Ladenburga.
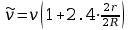
![]()
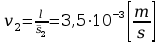
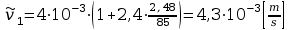
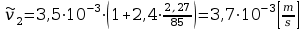
Wyznaczam teraz współczynnik lepkości dynamicznej:
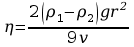
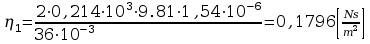
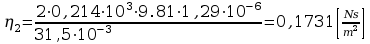
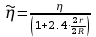
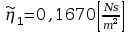
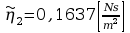
Błędy pomiarowe
Liczę błąd pomiaru pośredniego
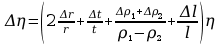
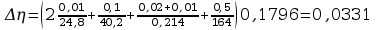
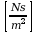
Ostatecznie:
η1
= (0,1796 ± 0,0331)
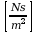
η1
= (0,1731 ± 0,0331)
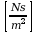
Wyszukiwarka
Podobne podstrony:
ćw, gik, semestr 4, Wyższa, Geodezja Wyższa, odstep geoidy cw7
cw7 cw 6 c d fir
ćw 4 Profil podłużny cieku
biofiza cw 31
Kinezyterapia ćw synergistyczne
Cw 1 ! komorki
Pedagogika ćw Dydaktyka
Cw 3 patologie wybrane aspekty
Cw 7 IMMUNOLOGIA TRANSPLANTACYJNA
Cw Ancyl strong
Cw 1 Zdrowie i choroba 2009
Rehabilitacja medyczna prezentacja ćw I
ćw 2b
Ćw 3 Elektorforeza Bzducha