Tomasz Pajączkowski

14.03.2001

Ćwiczenie nr 16.

Temat: Wyznaczanie lepkości cieczy za pomocą wiskozymetru Höpplera.

Celem ćwiczenia jest wyznaczenie dynamicznego współczynnika lepkości metodą Höpplera.

	τ [ s ]	ε² [ s² ]
1	10,08	0,0064
2	10,14	0,0004
3	10,20	0,0016
4	10,00	0,0256
5	10,17	0,0001
6	10,26	0,0100
7	10,11	0,0025
8	10,12	0,0016
9	10,26	0,0100
10	9,97	0,0361
11	10,21	0,0025
12	10,18	0,0004
13	10,24	0,0064
14	10,22	0,0036
15	10,11	0,0025
16	10,30	0,0196
17	10,12	0,0016
18	10,15	0,0001
19	10,22	0,0036
20	10,17	0,0001
	Σ 203,23	Σ 0,1347

Teoria zjawiska:

Ciecz zwilżająca pokrywa cienką warstwą ciała w niej zanurzone np. kulkę metalową. W przypadku, gdy kulka jest w ruchu, tarcie występuje wewnątrz samego płynu pomiędzy jego warstwami między kulką i płynem. Kulka unosi ze sobą warstwę przylegającego płynu, a ten na skutek tarcia wewnętrznego wprawia w ruch następne warstwy.

Jeżeli w dwóch stykających się ze sobą warstwach rzeczywistych płynów prędkości przepływającego płynu są różne, to obserwujemy stan przejściowy, podczas którego zachodzą procesy dążące do wyrównania prędkości w obu warstwach. Procesy te noszą nazwę tarcia wewnętrznego lub lepkości.

Spadek kulki w płynie ulega jednak znacznemu zwolnieniu w rurce o średnicy nieznacznie przekraczającej średnicę kulki ( z takim przypadkiem mamy do czynienia w przypadku wiskozymetru Höpplera ) . Wtedy rurę musimy ustawić nieco ukośnie, gdyż przy ustawieniu pionowym ruch kulki nie jest jednostajny. Przy ustawieniu skośnym kulka toczy się po ściance rurki. Do omówionego przypadku stosuje się równanie w postaci: η = K (ρK -ρP)t, ( 1 ) gdzie: K- stała przyrządu.

Kulka tocząc się porusza ze sobą warstewki cieczy w wąskiej szczelinie, jaka istnieje między kulką i ścianką rurki, występuje poślizg warstewki i pojawia się opór lepkości FL hamujący ruch kulki. Siła ta skierowana jest przeciwnie do prędkości V toczenia się kulki i zarówno FL jaki V są nachylone do pionu pod kątem α. Na kulkę działają, podobnie jak w wiskozymetrze Stokesa, trzy siły: składowa siły ciężkości, składowa siły wyporu oraz siła oporu lepkości.

Ruch kulki następuje zatem na skutek działania siły FG* =mg·cosα = =VρKg·cosα = 3/4·πr³ρKg cosα .

Ponieważ kulka spada w ośrodku płynnym, działa na nią siła wyporu ( zgodnie z prawem Archimedesa) FW *=-VρPg cosα =- 4/3·πr³ρPg cosα.

Sumując wszystkie siły działające na kulkę, otrzymujemy:

F* = 3/4·πr³ρKg cosα - 4/3·πr³ρPg cosα - kηrl/τ

Kulka porusza się ruchem jednostajnym, gdy F jest równe zeru ( I zasada dynamiki).

0 = 3/4·πr³ρKg cosα - 4/3·πr³ρPg cosα - kηrl/τ

3/4·πr³g( ρK - ρP) cosα = kηrl/τ

η =4r²gτ(ρK - ρP)·cosα/3kl

Przyjmując za 4πr²gcosα/3kl = K powyższy wzór przyjmuje postać:

η =K(ρK - ρP)τ ( 1 )

Opis metody:

Aparatura ( w sposób schematyczny pokazana na rysunku poniżej) składa się z rurki szklanej o promieniu R ustawionej pod kontem i umieszczonej w płaszczu wodnym ( umożliwia to utrzymanie stałej temperatury pomiaru ). Rurkę wiskozymetru napełniamy badaną cieczą, usuwając pęcherzyki powietrza powstałe na ściankach. Wkładamy kulkę i zamykamy rurkę korkami. Nastawiamy odpowiednią temperaturę na termometrze kontaktowym termostatu podłączonego do płaszcza wodnego, po czym, gdy temperatura się ustali przystępujemy do dokonania pomiaru.

Pomiaru dokonujemy mierząc czas w jakim kulka stoczy się po ściance rurki na drodze l, przy czym czas mierzymy od momentu przekroczenia przez kulkę górnej linii (A) zaznaczonej na rurce poziomym nacięciem do momentu przekroczenia przez kulkę dolnej linii (B). Następnie rurkę obracamy o kąt 180º i powtarzamy doświadczenie w sposób analogiczny.

Pomiar współczynnika lepkości można przeprowadzić w zależności od temperatury. Jest to możliwe dzięki użyciu termostatu utrzymującego stałą temperaturę badanej cieczy. Dla cieczy zależnością tą rządzi prawo: η(T) =A exp(B/T), gdzie: T -temperatura w skali Kelvina, A i B - stałe charakteryzujące ciecz.

Wzory robocze:

η = K (ρK -ρP)t, w przypadku wykonywania pomiaru zależności η(T) : η(T) =A exp(B/T).

Wykreślamy wówczas na papierze milimetrowym zależność log η (1/T). Korzystając z powyższego wykresu obliczamy stałe A i B z równania η(T) =A exp(B/T). W tym celu równanie to należy zapisać w postaci log η =B loge·1/T +logA ( y = ax +b ). Zatem nachylenie prostej ( a =B loge ) pozwoli wyznaczyć stałą B, a jej przecięcie z osią log η ( b= =logA ) pozwoli obliczyć stałą A. Zadanie sprowadza się do wyznaczenia nachylenia prostej i punktu przecięcia z osią log η.

Opis przeprowadzonego eksperymentu.

Przed przystąpieniem do wykonywania pomiaru należy starannie przemyć przyrząd benzenem, alkoholem lub eterem. Ciecz przeznaczoną do pomiaru należy wygotować, ochłodzić do temperatury pokojowej, a następnie napełnić nią rurkę usuwając pęcherzyki powstałe na ściance. Wkładamy kulki zamykamy rurkę wiskozymetru. Czynności tych nie

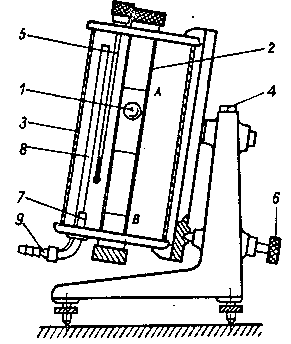
wiskozymetr Höpplera

wykonywałem ze względu na fakt, że użądzenie było już przygotowane do wykonywania pomiaru. Zatem pierwszą czynnością jaką wykonałem było wypoziomowanie aparatu. Następnie przystąpiłem do przeprowadzenia właściwego pomiaru.

Eksperyment wykonałem w sposób analogiczny jak zostało to przedstawione powyżej w opisie metody. Eksperyment został wykonany przez dwa zespoły, każdy z zespołów dokonał pomiaru czasu opadania kulki dla 10 prób. Po wykonaniu powyższego wyniki zostały zebrane w tabele i opracowane w sposób przedstawiony w tym sprawozdaniu.

Wykonując powyższe ćwiczenie nie wyznaczyliśmy zależności η(T) - nie było to bowiem celem ćwiczenia, dlatego w czasie wykonywanych obliczeń nie korzystałem z ostatnich zależności umieszczonych w poprzednim punkcie.

Obliczenia wykonane na podstawie zebranych wyników eksperymentalnych.

τ =1/n Σ τi =1/20·203,23 =10,16 s

Korzystając ze wzoru ( 1 )

η =0,00000007214·( 2395-988)·10,16 = 0,00102 Pa·s

Szacowanie niepewności pomiaru.

UB(τ) =0,01/3^1/2 =0,00577 s (ðη/ðK)² = (ρK -ρP)τ =2,0146·10⁸

^{UA(τ) =0,1347/20·(20-1) =0,000354 s (ðη/ðρK )² = K τ =5,37·10-13 UC(τ) = [ UA(τ)² + UB(τ)² ] 1/2 =0,00581 s (ðη/ ðρP)² = -Kτ =5,37·10-13}

UB(K) = 10^-11/3^1/2 =5,77·10^-12 m²/s² (ðη/ðτ)² = K (ρK -ρP) =1,007·10^-4

UB(ρ) =1/3^1/2 =0,577 kg/m³

UC(η) = [(ðη/ðK)²U²(K)+(ðη/ðρK )²U²(ρK)+(ðη/ðρP)²U²(ρP)+(ðη/ðτ)²U²(τ)] ^1/2 = 8,565·10^-7

U =2· 8,565·10^-7= 1,713·10^-6 dla α =0,95

η =(0,00102 ± 1,713·10^-6) Pa·s

Wnioski:

Wartość współczynnika lepkości wynosi ( 0,00102 ± 0,0023 ) Pa·s dla α =0,95. Świadczy to o dużej dokładności wykonanego ćwiczenia. Do takich wniosków można dojść, porównując otrzymaną ( średnią ) wartość współczynnika η z wartością odczytaną z tablic. Dla temperatury 25°C przyjmuje ona wartość 0,0008905 Pa·s .

Zatem wartość otrzymana przeze mnie w temperaturze 24,25°C winna być nieznacznie większa, wynika to z faktu, że współczynnik lepkości dla cieczy maleje ze wzrostem temperatury. Co jest zgodne z otrzymanym końcowym wynikiem eksperymentu. Potwierdza zatem to dużą dokładność wykonanego ćwiczenia.

Ewentualne błędy wynikają różnicy temperatury jaka w czasie wykonywania ćwiczenia; temperatura na początku eksperymentu wynosiła 23,5°C, po zakończeniu zaś 25°C. Fakt ten wynikał na skutek promieniowania cieplnego z otoczenia. Duży wpływ odgrywa tu również fakt, że ćwiczenie wykonywane było przez dwa zespoły (każdy zespół dokonał po 10 pomiarów ), co skutkuje różną dokładnością otrzymanych zestawów wyników.

Wiskozymetr Höpplera dzięki rozwiązaniom technicznym takim jak zamknięcie rurki z cieczą, możliwość utrzymywania stałej temperatury przy podłączeniu termostatu oraz fakt, że przy wyznaczaniu współczynnika η używa się cały czas tej samej kulki, pozwala na otrzymywanie bardzo dokładnych ( powtarzających się ) wyników co stanowi zaletą tego przyrządu.

wg "Tablic chemicznych" Wydanie II, zmienione i rozszerzone Warszawa 1997

Stałe:

ρK = 0,998·10³ kg/m³

ρP =2,395·10³ kg/m³

K= 7,214·10^-8 m²/s²

Średnia temperatura w czasie wykonywania ćwiczenia wynosiła: T = 0,5 ( T1+T2 ) =24,25°C

T1= 23,5°C

T2= 25°C

1- kulka szklana

2- rurka szklana

3- obudowa

4- poziomica służąca do kontroli ustawienia przyrządu

5- termometr

6- śruba służąca do unieruchomienia rurki

7- króciec doprowadzający czynnik grzewczy do płaszcza grzejnego

8- króciec odprowadzający czynnik grzewczy

9- króciec wyprowadzenia do termostatu

---