Ćwiczenie 5

ZASADY REGULACJI

5.1 Typy regulatorów

Poprawne działanie układu regulacji zależy od doboru odpowiedniego typu regulatora do obiektu regulacji. Przyjęty typ regulatora określa zasadę regulacji, tzn. zależność wiążącą sygnał odchyłki e z sygnałem sterującym u. W regulatorach ciągłych ta zależność opiera się na proporcjonalności, całkowaniu i różniczkowaniu odchyłki e.

Najczęściej wykorzystywane w praktyce typy regulatorów to:

1. regulator proporcjonalny P

(5.1)

(5.2)

2. regulator całkujący I

(5.3)

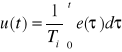
(5.4)

3. regulator proporcjonalno - całkujący PI

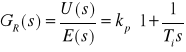
(5.5)

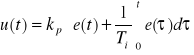
(5.6)

4. regulator proporcjonalno - różniczkujący PD

(5.7)

(5.8)

5. regulator proporcjonalno - całkująco - różniczkujący PID

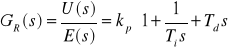
(5.9)

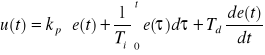
. (5.10)

Współczynniki występujące w równaniach definiujących poszczególne typy regulatorów nazywa się nastawami. Nastawy posiadają standardowe nazwy: k_p współczynnik wzmocnienia, T_i - czas zdwojenia, T_d - czas wyprzedzenia.

Oznaczenia poszczególnych typów regulatorów pochodzą od pierwszych liter angielskich nazw poszczególnych operacji (P - proportional, I - integration, D - differentiation). Możliwe są również inne kombinacje powyższych działań, ale nie są one stosowane w praktyce.

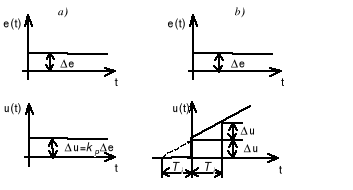
Rys. 5.1 Charakterystyki skokowe regulatorów: a) regulator P, b) regulator PI

Na podstawie zarejestrowanych charakterystyk skokowych można wyznaczyć rzeczywisty współczynnik wzmocnienia regulatora

(5.11)

Z charakterystyki skokowej regulatora PI można ponadto wyznaczyć T_i. Czas zdwojenia T_i jest to czas od momentu zaistnienia skokowej zmiany odchyłki do chwili, gdy sygnał wyjściowy z regulatora PI osiągnie dwukrotną wartość sygnału, którą otrzymano by w regulatorze bez działania całkującego (regulator P).

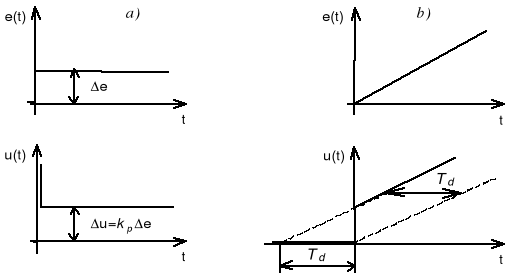
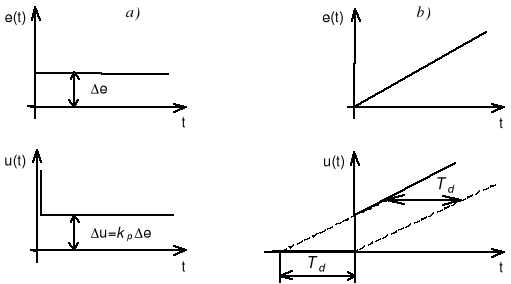
Rys. 5.2 a) charakterystyka skokowa regulatora PD, b) odpowiedź regulatora PD na sygnał liniowo narastający

Czas wyprzedzenia regulatora PD można wyznaczyć z odpowiedzi na sygnał liniowo narastający. Czas wyprzedzenia T_d jest to czas o jaki sygnał wyjściowy z regulatora PD wyprzedza sygnał wyjściowy z regulatora P przy liniowo narastającej zmianie odchyłki.

W praktyce bardzo trudno jest zrealizować idealnie operację różniczkowania. Stąd też operację różniczkowania realizuje się jako różniczkowanie z inercją. Otrzymuje się wtedy tzw. rzeczywiste regulatory PD (5.12) i PID (5.13). Regulatory określone wzorami (5.7) i (5.9) nazywa się regulatorami idealnymi.

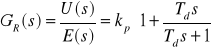
(5.12)

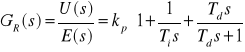
(5.13)

Zmieniając odpowiednio nastawy regulatora PID można uzyskać regulatory o mniej złożonej strukturze. Np. przyjmując T_d = 0 oraz
, otrzymuje się regulator typu P.

Tabela 5.1

Charakterystyki regulatorów przy wymuszeniu skokowym i liniowym

5.2 Własności układów regulacji

Regulator G_R(s) jest dołączany do obiektu G_O(s) w pętli ujemnego sprzężenia zwrotnego. Zmienia to dynamikę oddziaływań (równanie różniczkowe) w torze zakłócenie Z(s) - wielkość regulowana Y(s). Można to sformułować w ten sposób, że dołączenie regulatora powoduje transformację układu G_O(s) w układ G_W(s) (rys. 5.3).

Z(s) Y(s) Z(s) Y(s)

Z(s) Y(s)

Rys. 5.3. Transformacja układu przez dołączenie sprzężenia zwrotnego

(5.14)

Własności dynamiczne układu regulacji będą ilustrowane m. in. za pomocą przebiegów przejściowych. Przebieg przejściowy jest to odpowiedź układu regulacji wywołana skokiem jednostkowym zakłócenia.

W przedstawionych poniżej przykładach zostanie przeanalizowany sposób oddziaływania poszczególnych regulatorów na obiekt pierwszego rzędu o transmitancji:

,
. (5.15)

Jeżeli a=0, to jest to obiekt całkujący. Dla a>0 jest to obiekt inercyjny o stałej czasowej
i współczynniku wzmocnienia
.

Układ z regulatorem P.

Transmitancja wypadkowa układu z rys. 5.3 dla obiektu (5.15) i regulatora (5.1) wynosi :

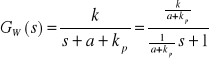
. (5.16)

Dołączenie regulatora proporcjonalnego nie zmieniło rzędu obiektu. Ponad to dla dowolnej dodatniej wartość k_p, układ (5.16) jest inercją pierwszego rzędu, której współczynnik wzmocnienia i stałą czasową można dowolnie zmniejszać poprzez zwiększanie k_p. Nie mniej jednak nie można znaleźć takiej wartości k_p, żeby ten współczynnik wzmocnienia był równy zero. W wyniku tego stałe zakłócenie wywołuje trwałą zmianę wielkości wyjściowej w stanie ustalonym.

Przebieg przejściowy wywołany skokową zmianą zakłócenia z(t)=1(t) jest następujący :

(5.17)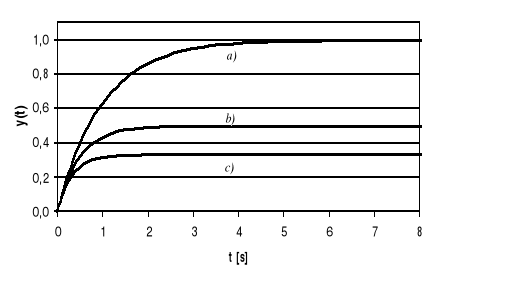

Rys. 5.4. Przebiegi przejściowe obiektu inercyjnego z regulatorem proporcjonalnym

dla a= 1 , k= 1; a) k_p= 0, b) k_p= 1, c) k_p= 2

Układ z regulatorem I.

Transmitancja układu regulacji dla obiektu (5.15) i regulatora całkującego wynosi :

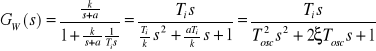
(5.18)

gdzie

.

Dołączenie regulatora całkującego spowodowało, że rząd układu wzrósł o jeden. Otrzymany układ ma własności dynamiczne członu oscylacyjnego z różniczkowaniem. Zmniejszając stałą czasową całkowania T_i można skracać stałą czasową oscylacji T_osc. Jednak powoduje to jednocześnie zmniejszanie współczynnika tłumienia ξ, co prowadzi do wzrostu amplitudy oscylacji. Ponad to jeżeli współczynnik obiektu a = 0, to powyższy układ regulacji jest niestabilny strukturalnie. Nie można wówczas dobrać stałej T_i, tak aby oscylacje układu były tłumione. Z tych względów regulatora I nie stosuje się w praktyce. Jednak zaletą działania całkującego jest to, że współczynnik wzmocnienia układu (5.18) jest równy zero. Oznacza to, że jeżeli zakłócenie jest stałe, to niezależnie od jego wartości wielkość regulowana będzie równa zero w stanie ustalonym. Aby zapewnić szybkie i pewne osiąganie stanu ustalonego działanie całkujące łączy się z działaniem proporcjonalnym.

Przebieg przejściowy układu (5.18)

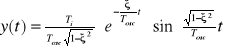
(5.19)

Przebieg przejściowy (5.19) dla a=0.

(5.20)

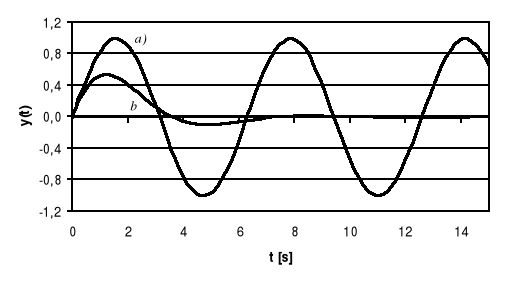
Rys. 5.5. Przebiegi przejściowe z regulatorem całkującym dla T_i=1, k=1;

a) a=0, b) a=1

Układ z regulatorem PI

Transmitancja wypadkowa układu regulacji dla obiektu (5.15) i regulatora PI wynosi:

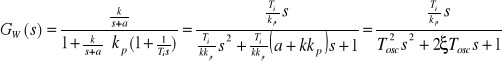
(5.21)

gdzie

.

Podobnie jak przy dołączeniu regulatora I, również i w tym przypadku rząd układu wzrósł o jeden. Otrzymany układ ma własności dynamiczne członu oscylacyjnego z różniczkowaniem. Współczynnik wzmocnienia jest równy zero. Jednakże w tym przypadku do dyspozycji są dwie nastawy, co pozwala niezależnie zmieniać stałą czasową T_osc i współczynnik tłumienia ξ. Można tak dobrać nastawy regulatora PI, że ξ>1. Wtedy układ ma własności członu inercyjnego drugiego rzędu z różniczkowaniem. Po skokowej zmianie zakłócenia układ osiągnie ten sam punkt równowagi, w którym był przed zakłóceniem, lecz bez oscylacji.

Przebieg przejściowy dla układu (5.21) przy ξ>1.

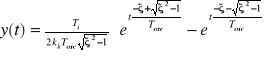
(5.22)

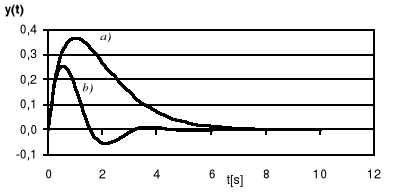
Rys. 5.6. Przebiegi przejściowe z regulatorem PI dla k=1, a=1, k_p=1

a) T_i = 1, ξ>1 b) T_i = 0.2, ξ<1

5.3 Zadania do wykonania

1. Zamodelować w Simulinku regulator o zadanej strukturze

1. korzystając z gotowych operacji całkowania i różniczkowania

2. korzystając z modułu Transfer Function

2. Wydrukować charakterystyki skokowe zadanego regulatora i na ich podstawie sprawdzić wartości nastaw.

3. Zbadać symulacyjnie wpływ nastaw k_p i T_i regulatora P, I, PI na przebieg przejściowy układu regulacji z obiektem inercyjnym lub całkującym.

Rys. 5.7. Zestaw bloków używanych podczas ćwiczenia

5.4 Pytania kontrolne

1. Podać transmitancje i charakterystyki skokowe poszczególnych typów regulatorów

2. Co to są nastawy? Podać ich nazwy.

3. Co można uzyskać przez zastosowanie działania całkującego w prawie regulacji.

4. Obliczyć transmitancję wypadkową układu regulacji dla obiektu I-go rzędu.

5. Co to jest niestabilność strukturalna układu regulacji.

5.5 Literatura

[1] Chorowski B., Werszko M., Automatyzacja procesów przemysłowych, Podstawy. Wyd. PWr. Wrocław 1980

G_W(s)

G_O(s)

G_R(s)

G_O(s)

---