4.DYNAMIKA PŁYNU DOSKONAŁEGO

Dynamika płynu doskonałego zajmuje się opisem ruchu wyidealizowanego, nielepkiego (
) płynu, w którym naprężenia styczne nie występują.

Głównym zadaniem dynamiki płynu doskonałego jest wyznaczenie sił powierzchniowych, z jakimi płyn oddziaływa na ciało znajdujące się w polu przepływu lub na ścianki przewodu, przy zadanym polu jednostkowych sił masowych. Zadaniem pośrednim, pozwalającym zrealizować cel główny jest określenie skalarnego pola ciśnień dynamicznych (hydrodynamicznych) p=p(x,y,z,t)

4.1. Równania różniczkowe ruchu płynu doskonałego - Eulera.

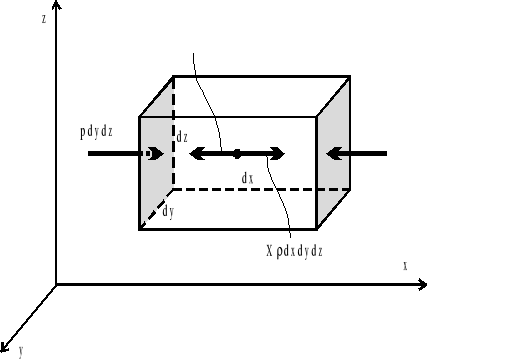
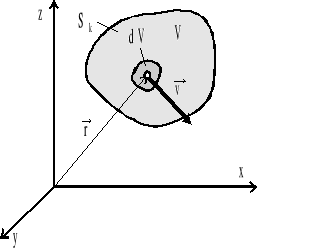
Wyodrębnijmy element płynu w kształcie prostopadłościanu o wymiarach dx,dy,dz (rys.4.1), poruszającego się w polu jednostkowych sił masowych
z przyspieszeniem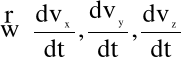
.

Rys.4.1. Wyodrębniony element płynu doskonałego.

Oznacza to zastąpienie „odrzuconej” części płynu siłami powierzchniowym(ciśnieniami) działającymi na każdą ze ścianek elementu płynu. Z bilansu sił (ciśnień) działających na element płynu w kierunku osi x wynika równanie:

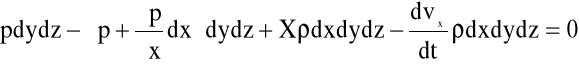
(4.1)

a zatem

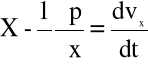
(4.2)

Postępując analogicznie, tzn. dokonując bilansu sił w kierunkach osi y i z oraz rozwijając pochodne substancjalne występujące po prawej stronie uzyskanych w ten sposób równań otrzymujemy równania różniczkowe ruchu płynu doskonałego - Eulera:

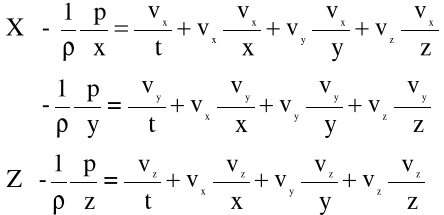
(4.3)

W zapisie skróconym równania (4.3) przyjmują postać:

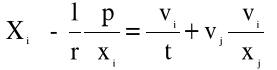
(4.3a)

wobec tego należy uzupełnić je czwartym równaniem - równaniem ciągłości:

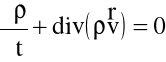
(4.4)

4.2. Równania różniczkowe ruchu płynu doskonałego w postaci Gromeki-Lamba.

Przekształćmy pierwsze z równań Eulera w sposób następujący:

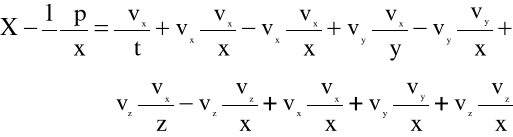
Stąd

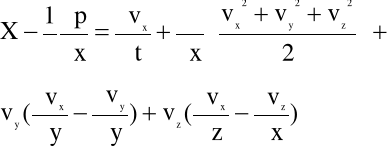
(4.5)

Pamiętając, że:

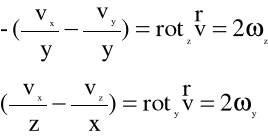
(4.6)

mamy:

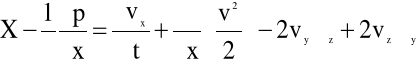
(4.7)

Załóżmy, że:

1/ jednostkowe siły masowe mają potencjał, tj.

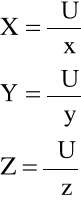
(4.8)

2/ płyn jest barotropowy, tzn.
.

Wprowadźmy tzw. funkcję ciśnienia Gromeki P=P(x,y,z,t), taką, że:

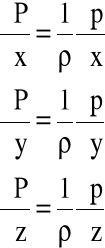
(4.9)

wtedy

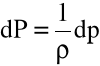
(4.10)

Podstawiając powyższe związki do równań ruchu mamy:

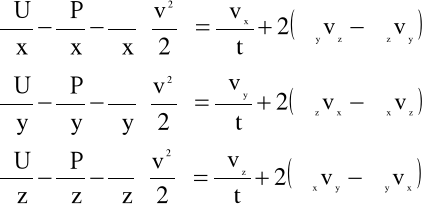
(4.11)

Mnożąc pierwsze z równań (4.9) przez dx, drugie - przez dy i trzecie - przez dz, a następnie sumując stronami te równania otrzymujemy:

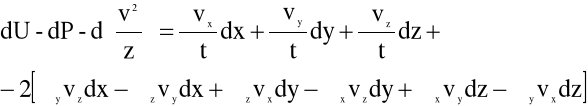
(4.12)

lub

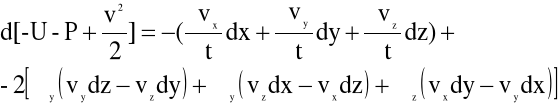
lub

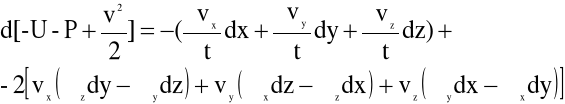
(4.12)

Otrzymaliśmy w ten sposób tzw. równanie Gromeki - Lamba

4.3. Całki różniczkowych równań ruchu płynu doskonałego

4.3.1 Całka Lagrange'a - Cauchy'ego

W przypadku nieustalonego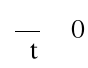
ruchu potencjalnego
mamy:

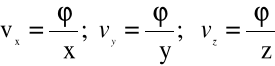
(4.13)

Zatem

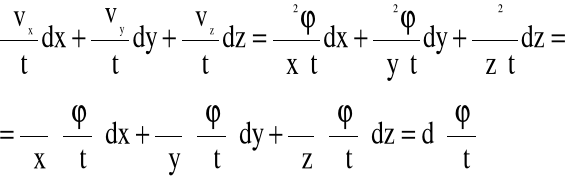
W świetle powyższego równanie Gromeki - Lamba przyjmuje postać;

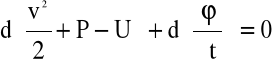
(4.14)

lub po scałkowaniu,

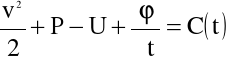
(4.15)

Równanie (4.15) nosi nazwę całki Lagrange'a-Cauchy'ego.

4.3.2. Całka Bernoulli'ego

Po scałkowaniu równania Gromeki-Lamba, przy założeniu, że jego prawa strona jest równa zeru, otrzymujemy tzw. całkę Bernoulli'ego:

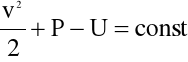
(4.16)

Całka Bernulli'ego obowiązuje w przypadku ruchu ustalonego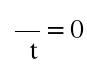

oraz ruchu:

1. - potencjalnego
   lub

2. - wirowego, dla punktów leżących na jednej linii prądu lub na jednej linii wiru.

Załóżmy, że

1/ Ruch odbywa się w potencjalnym polu grawitacyjnym sił masowych, tzn.

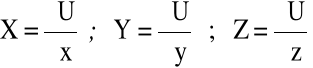
(4.17)

2/ Ruch odbywa się wzdłuż określonej linii prądu, tzn.

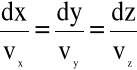
(4.18)

3/ Ruch jest ustalony, tzn.

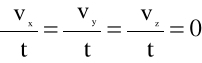
(4.18)

4/ Płyn jest barotropowy, tzn. istnieje taka funkcja P=P(x,y,z), że

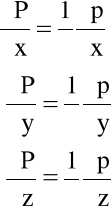
(4.19)

wtedy

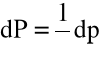
(4.20)

Przekształćmy pierwsze z równań Eulera (4.3), tj:

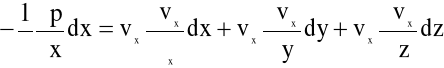
Mamy:

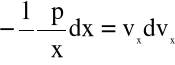
Wracając do równań (4.3) i postępując analogicznie otrzymujemy układ równań:

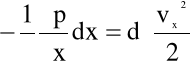
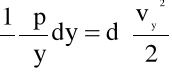
(4.21)

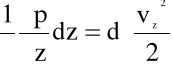
Po dodaniu stronami równań (4.21) otrzymujemy równanie różniczkowe:

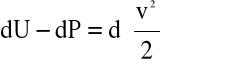
(4.22)

lub

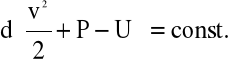
(4.23)

Po scałkowaniu równania (4.23) otrzymujemy tzw. całkę Bernoulli'ego:

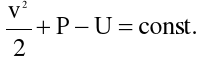
(4.24)

4.4. Równanie Bernoulli'ego

Szczególnym przypadkiem całki Bernoulli'ego, gdy ruch płynu odbywa się w polu grawitacyjnym ziemskim ( X=Y=0 ; Z= -g ), (por. 2.17), tzn.

dU=-gdz+C (2.17)

jest równanie Bernoulli'ego:

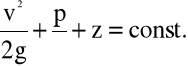
(4.25)

lub

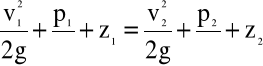
(4.26)

przy czym, w przypadku strugi cieczy o przekroju skończonym obowiązuje równanie ciągłości (3.49), tj.

(3.49)

4.4.1. Interpretacja fizykalna równania Bernoulli'ego

Równanie Bernoulli'ego przedstawia zasadę zachowania energii w odniesieniu do elementarnej strugi cieczy.

Faktycznie:

- jest właściwą (odniesioną do jednostki masy) energią kinetyczną strugi,

+gz - jest właściwą energią potencjalną

Suma energii kinetycznej i potencjalnej (odniesionych do jednostki masy) jest stała w każdym przekroju strugi płynu doskonałego.

4.4.2.Interpretacja geometryczna równania Bernoulli'ego

Oznaczmy:

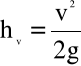
, (4.50)

którą dalej nazywać będziemy wysokością prędkości,

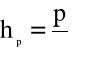
(4.51)

nazywaną wysokością ciśnienia

i

z, (4.52)

którą nazywać będziemy dalej wysokością niwelacyjną lub wysokością położenia.

Równanie Bernoulli'ego (4.26) możemy przepisać w postaci:

(4.53)

Interpretację geometryczna równania Bernoulli'ego przedstawiono na rys.4.2.

Rys.4.2. Interpretacja geometryczna równania Bernoulli'ego dla płynu doskonałego.

Stwierdzamy zatem, że:

Suma wysokości: prędkości, ciśnienia i położenia jest stała w dowolnym przekroju strugi (elementarnej) cieczy.

Z uwagi jednak na fakt, że w przypadku przepływu płynu doskonałego nie występuje tarcie wewnętrzne, prędkość w dowolnym punkcie przekroju skończonego przekroju przewodu (np. rury) jest stała (jednorodna) i równa średniej prędkości przepływu, dlatego równanie Bernoulli'ego dla przepływu cieczy doskonałej w przewodach o zmiennym przekroju poprzecznym można przedstawić w postaci:

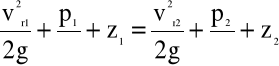
(4.54)

przy czym obowiązuje równanie ciągłości (3.49) w postaci

(4.55)

4.5. Przykłady zastosowań równania Bernoulli'ego

4.5.1. Pomiar prędkości lokalnej za pomocą rurki Prandtla

Rozważmy opływ ciała stałego płynem (rys. 4.3.). W szczególnym przypadku (rozdz. 3.3) w punktach natarcia „N” i spływu „S” centralna linia prądu przecina się z konturem opływanego ciała, który traktować można jako linię prądu, na której prędkość v=0.

Rys. 4 3. Opływ ciała stałego płynem.

Równanie Bernoulli'ego dla punktu „1” oddalonego nieskończenie daleko od punktu natarcia „2” i punktu natarcia 2 ma postać:

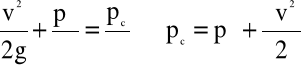
(4.56)

gdzie:

(4.57)

jest ciśnieniem statycznym,

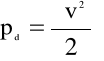
(4.58)

jest ciśnieniem dynamicznym, natomiast

jest prędkością lokalną.

Zatem

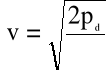
(4.59)

Na rys.4.4. przedstawiono schemat rurki Prandtla.

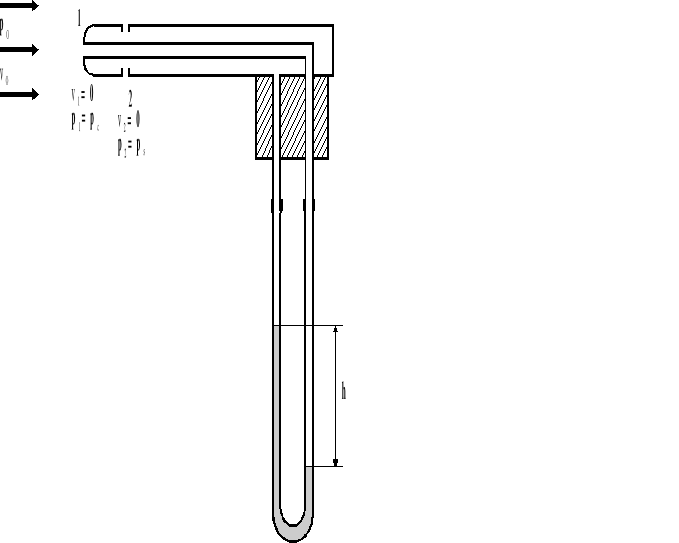
Rys.4.4. Rurka Prandtla.

Rurka piętrząca Prandtla służy pośrednio do pomiaru prędkości lokalnej gazu.

Przy zastosowaniu manometru cieczowego dokonuje się pomiaru ciśnienia dynamicznego

(4.60)

i na tej podstawie oblicza się prędkość lokalną

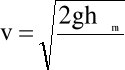
(4.61)

gdzie γ_m jest ciężarem właściwym cieczy manometrycznej, natomiast γ - ciężarem właściwym przepływającego płynu.

4.5.2. Pomiar natężenia przepływu za pomocą zwężki Ventouri'ego

Zwężka Ventouri'ego składa się z konfuzora, krótkiego odcinka o stałej średnicy d i dyfuzora. Zwężka instalowana jest w przewodzie o średnicy D>d, w którym ma miejsce przepływ płynu (rys.4.5). i służy do pośredniego pomiaru objętościowego strumienia przepływu (objętościowego wydatku przepływu).

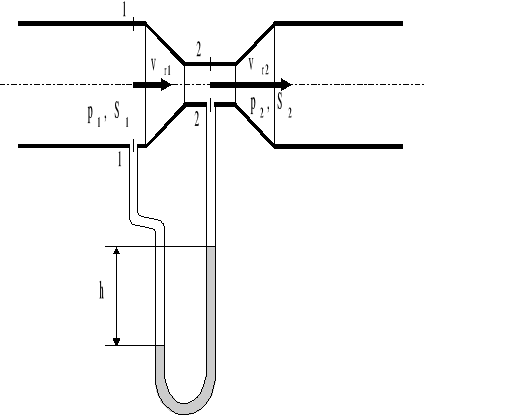
Rys.4.5. Schemat zwężki Ventouri'ego

Zgodnie z równaniem Bernoulli'ego (4.54), zapisanym dla przekrojów „1” i „2” mamy

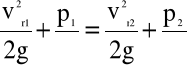
(4.62)

oraz po uwzględnieniu równania ciągłości (4.55), z którego wynika, że

(4.63)

gdzie stała zwężki

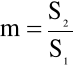
(4.64)

Po uwzględnieniu (4.43) w (4.62) otrzymujemy wzór określający średnią prędkość przepływu w przewodzie głównym

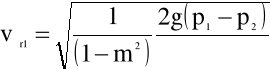
(4.65)

lub objętościowy strumień przepływu

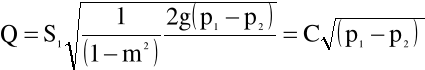
(4.66)

4.5.3. Lewar - zjawisko kawitacji

Na rys.4.6. przedstawiono przepływ cieczy w rurce ze zbiornika górnego do zbiornika dolnego po uprzednim zassaniu cieczy. Zakrzywioną rurkę wprowadzoną jednym końcem do naczynia (górnego), w celu umożliwienia wypływu cieczy nazywamy lewarem.

Napiszmy równanie Bernoulli'ego dla przekrojów „0” i „2”strugi cieczy.

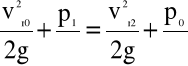
(4.67)

Założymy, że pole powierzchni swobodnej w zbiorniku górnym S₀ jest dużo większe od przekroju rurki lewara f. Wykorzystując równanie ciągłości (4.55) mamy:

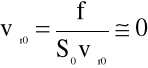
Wtedy średnia prędkość przepływu w lewarze:

(4.68)

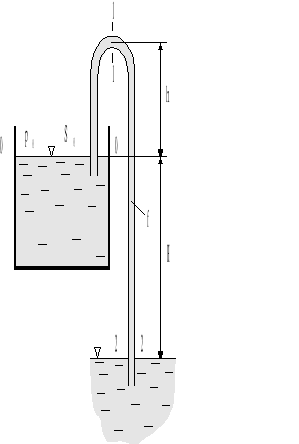
Rys.4.6. Lewar.

Z kolei, z równania Bernoulli'ego zapisanego dla przekrojów „1” i „2”

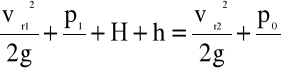
(4.69)

wynika, że ciśnienie w przekroju „1” lewara wynosi:

(4.70)

Wyciągamy zatem wniosek, że p₁<p₀

Przy pewnej, dostatecznie dużej wysokości h ciśnienie p₁ może obniżyć się do ciśnienia wrzenia p_v w temperaturze otoczenia i zaczną wytwarzać się pęcherzyki pary w kolanie lewara (przekroju „1”).

Po wytworzeniu się pary ciśnienie wzrasta i następuje jej skroplenie. Zjawisko takie, mające charakter okresowo zmienny nazywamy kawitacją. Towarzysząca kawitacji korozja i drgania akustyczne są zjawiskami niepożądanymi i niebezpiecznymi, których należy unikać.

4.5.4. Wypływ ustalony cieczy ze zbiornika przez mały otwór

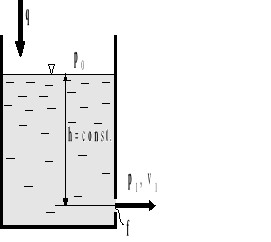
Rys.4.7. Ustalony wypływ cieczy ze zbiornika przez mały otwór.

Zbadajmy ustalony (rys.4.7) wypływ cieczy ze zbiornika przy założeniu, że przekrój otworu wypływowego jest mały.

Warunkiem gwarantującym stacjonarność wypływu jest stałość poziomu cieczy w zbiorniku, tj. h= const. Warunek ten spełniony jest wtedy, gdy strumienie objętościowe cieczy: wpływającej i wypływającej ze zbiornika są takie same. Oznacza to, że
.

Z równania Bernoulli'ego zapisanego dla przekrojów „0” i „1” (rys.4.7)

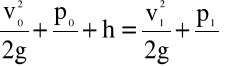
(4.71)

wynika, że

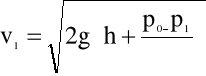
(4.72)

W przypadku gdy
mamy:

(4.73)

Jest to, tzw. wzór Toricellego, określający teoretyczną prędkość wypływu cieczy doskonałej.

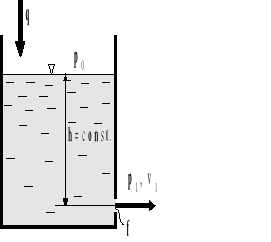
Rys.4.7. Ustalony wypływ cieczy ze zbiornika przez mały otwór.

Prędkość wypływu cieczy rzeczywistej obliczyć można za pomocą wzoru

(4.74)

gdzie ϕ - współczynnik poprawkowy prędkości uwzględniający lepkość płynu i charakter wypływu.

Rzeczywisty wydatek wypływu (rys.4.7) wynosi

(4.75)

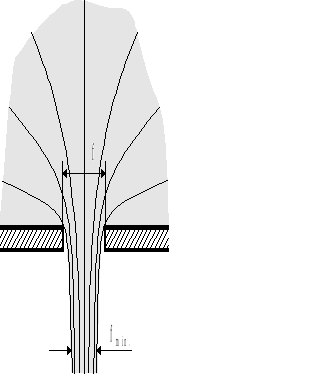
Rys.4.8. Zjawisko kontrakcji.

Wprowadzając tzw. współczynnik poprawkowy kontrakcji

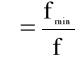
(4.76)

otrzymujemy wzór określający objętościowy strumień wypływu cieczy rzeczywistej:

(4.77)

gdzie

(4.78)

jest tzw. współczynnikiem poprawkowym wydatku wypływu.

4.5.5. Czas wypływu nieustalonego cieczy ze zbiornika przez mały otwór

Wypływ nieustalony cieczy ze zbiornika (rys.4.9.) ma miejsce wtedy, gdy:

1/
- poziom cieczy w zbiorniku opada,

2/
- poziom cieczy w zbiorniku podnosi się.

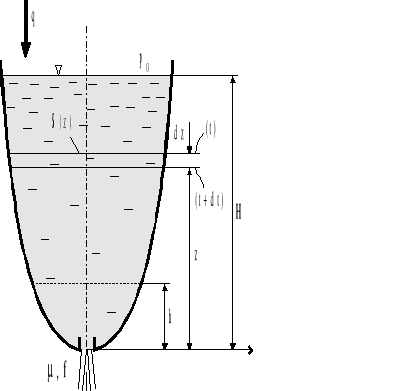
Rys.4.9. Nieustalony przepływ cieczy ze zbiornika przez mały otwór.

Bilans masy cieczy wypływającej i dopływającej do zbiornika w czasie dt jest następujący:

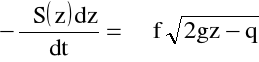
Stąd

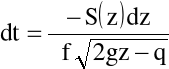
Czas częściowego opróżniania zbiornika obliczyć, zatem, można za pomocą wzoru:

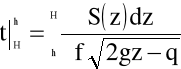
(4.79)

Czas całkowitego opróżniania zbiornika określa z kolei wzór:

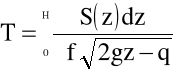
(4.80)

4.6. Zasada pędu w mechanice płynów

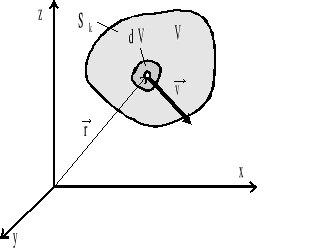
Rozważmy ustalony ruch płynu nieściśliwego (rys.4.10).

Rys.4.10. Obszar płynny płynu

Pęd elementu płynu o objętości dV:

(4.81)

Pęd bryły cieczy o objętości płynnej V wynosi:

(4.82)

Zgodnie z zasadą pędu mamy:

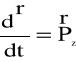
(4.83)

lub, po kolejnych przekształceniach:

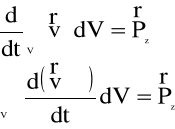
Ponieważ jednak założyliśmy wcześniej, że ruch cieczy jest ustalony, zatem:

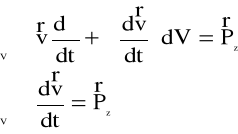
Zrzutujemy to równanie w kierunku osi x. Mamy:

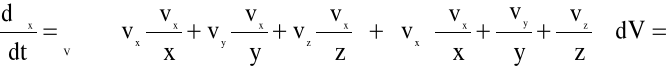
(4.84)

Pochodną

obliczyć zatem można w sposób następujący:

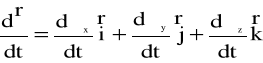
(4.85)

Wracając do równania (4.83) otrzymujemy wzór:

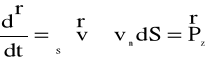
(4.86)

lub

(4.87)

Wzór (4.87) opisuje tzw. reakcję hydrodynamiczną, (napór hydrodynamiczny), tj. sięłę poruszająca się ciecz oddziaływa na ściankę ciała stałego.

4.7. Napór hydrodynamiczny cieczy na ściankę krzywaka

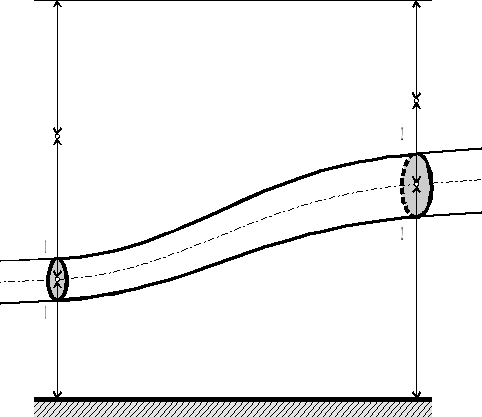
Zakrzywiony przewód o zmiennym przekroju poprzecznym (rys.4.10) nazywać będziemy krzywakiem.

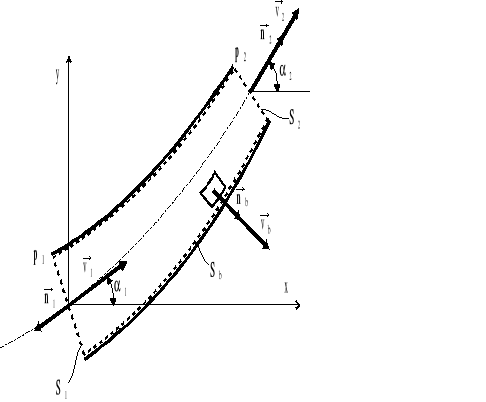
Rys.4.11. Ruch jednowymiarowy cieczy w krzywaku.

Zgodnie z zasadą pędu:

(4.88)

Zatem w rozważanym przypadku

(4.89)

Ponieważ powierzchnia ograniczająca rozważany obszar

(4.90)

otrzymujemy:

(4.91)

Ale

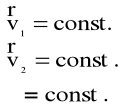
Stąd

Zatem

(4.92)

Oznaczmy
; jest to reakcja hydrodynamiczna (napór hydrodynamiczny cieczy na ściankę krzywaka). W świetle powyższego, po przekształceniu równania (4.92) otrzymujemy wzór opisujący wypadkowy wektor reakcji hydrodynamicznej na ścianki krzywaka.

(4.92a)

Zakładając, że krzywak usytuowany jest w płaszczyźnie xy, możemy obliczyć składowe reakcji hydrodynamicznej:

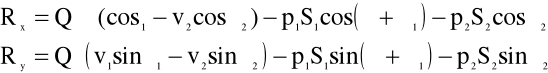
(4.93)

4.8. Zasada, krętu w mechanice płynów

Podobnie jak w p.4.6. rozważymy ustalony ruch płynu nieściśliwego o objętości V.

Rys.4.10. Obszar płynny płynu

Kręt elementu o objętości dV (rys.4.10).

(4.95)

lub

(4.96)

Zgodnie z zasadą krętu:

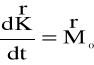
(4.97)

Zatem

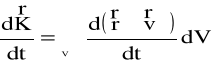
(4.98)

Ale

(4.99)

Po zrzutowaniu równania (4.98) w kierunku osi x ,mamy:

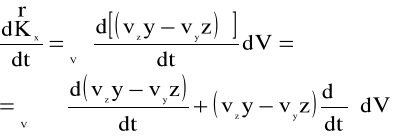
(4.100)

Z kolei, zgodnie z założeniem nieściśliwości płynu ρ=const, otrzymujemy:

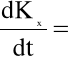
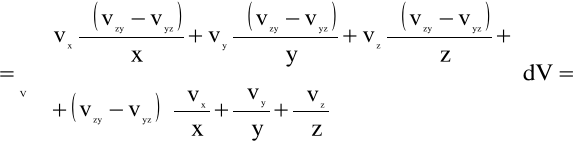
(4.101)

i następnie

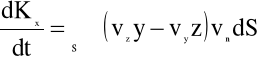
(4.102)

Zasadę krętu w mechanice płynów sformułować można w postaci równania:

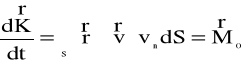
(4.103)

gdzie
jest momentem głównym sił zewnętrznych działających na rozważany obszar płynu. Moment reakcyjny:

. (4.104)

z₁

z₂

---