Politechnika Śląska

Wydział AEiI

Kierunek AiR

Ćwiczenia laboratoryjne z fizyki

Wyznaczanie prędkości dźwięku w powietrzu metodami :

-rezonansową

-przesunięcia fazowego

-Quinckego

Grupa 3

Sekcja 10

Rafał Papiernik

Tomasz Nowak

Tomasz Sobański

Gliwice 26-03-1999

1)Wstęp.

W powietrzu jak w każdym innym gzie drgania dźwiękowe rozchodzą się pod postacią fal podłużnych , są to rozchodzące się rozrzedzenia i zagęszczenia ośrodka. Ze względu na durzą prędkość rozchodzenia są to przemiany adiabatyczne. Jest to zaburzenie które może rozchodzić się tylko w ośrodku sprężystym. Polega ono na przenoszeniu energii przez drgające cząsteczki ośrodka bez zmiany ich średniego położenia. Prędkość rozchodzenia się fal dźwiękowych zależy od rodzaju ośrodka , temperatury oraz wilgotności.

Prędkość dźwięku w powietrzu wynosi 331 [m/s].

Pomiar prędkości dźwięku stosowanymi przez nas metodami opiera się na zjawisku fali stojącej. Jest to zjawisko polegające na interferencji dwóch biegnących naprzeciw siebie fal o jednakowych amplitudach. W określonych punktach amplituda fali stojącej równa się sumie amplitud obydwu drgań składowych ,nazywają się one strzałkami. W innych punktach amplituda wypadkowa wynosi zero , są to węzły.

2)Przebieg ćwiczenia .

a)Metoda rezonansowa

- ustawiamy odległość mikrofonu od głośnika kolejno na 20 cm , 30 cm , 40 cm.

Zwiększając częstotliwość dla każdej odległości szukamy na ekranie oscyloskopu trzech kolejnych maksymalnych wartości sygnału i zapisujemy odpowiadającą im częstotliwość.

b)Metoda przesunięcia fazowego

Ustawiamy częstotliwość kolejno na 1503 Hz , 1800 Hz , 2101 Hz. Dla każdej częstotliwości zmieniamy odległość mikrofonu od głośnika aż do momentu kiedy elipsa przejdzie w linie prostą - zapisujemy tą odległość i szukamy następnej .

c)Metoda Quinckego

Ustawiamy częstotliwość na 1001 Hz. Napełniamy rurę wodą a następnie odkręcając zawór powoli obniżamy jej poziom . Notujemy kolejne położenia poziomu wody odpowiadające maksymalnemu natężeniu dźwięku. Czynność tę

wykonujemy trzykrotnie.

3) Opracowanie wyników.

a) Metoda rezonansowa.

Ze względu na duże zakłócenia utrudniające odczyt kolejnych maksimów z oscyloskopu i wynikające z tego absurdalne wyniki odrzuciliśmy pomiary wykonane dla odległości 20 cm.

Prędkość dźwięku odliczyliśmy ze wzoru:

c = 2 l ( f1 -f0 ) i c = 2 l ( f2 -f1 )

Błędy obliczyliśmy z różniczki zupełnej , otrzymaliśmy wzór:

c = | 2 ( f1-f0 ) | | l | + | 2 l | |f | i c = | 2 ( f2-f1 ) | | l | + | 2 l | |f |

Δl= ± 0,5 cm. Δf= ±0,5%

Po wstawieniu danych otrzymaliśmy:

Lp.	Prędkość dźwięku c [m/s]	błąd Δc [m/s]
1	56,4	4,4
2	213,6	8,1
3	350,4	11,3
4	316,8	12,4

Pierwszy wynik odrzucamy gdyż daleko odbiega od rzeczywistości. Pozostałe wyniki uśredniamy stosując metodę średniej warzonej i w wyniku otrzymujemy:

c=272,5 ± 5,8[m/s]

Następnie obliczamy wykładnik adiabaty χ z wzoru

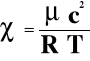
gdzie:

R = 8.31 [J/ (mol K)],

μ = 28.87*10-3 [kg/mol]

T = 24[C] = 297 ± 0,5[ K]

c= wyliczona przez nas prędkość dźwięku

Błąd obliczyliśmy z wzoru

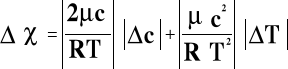
χ=0,87±0,04

b)Metoda przesunięcia fazowego.

Do obliczenia prędkości oraz błędu jego wyznaczenia zastosowano następujące wzory :

c= 2 f  l  l 

c =2 | ( l  l ) |f | + | 2f | | l |

Δl= ±0,5[m]

Częstotliwość [Hz]	1503		1800				2101
nr	c	c	C	c	c	c
1	342,7	16,7	342,0	19,7	344,6	22,7
2	345,7	16,8	345,6	19,7	344,6	22,7
3	345,7	16,8	349,2	19,7	348,8	22,7
4	-	-	345,6	19,7	344,6	22,7
5	-	-	-	-	348,8	22,8

Wyniki te uśredniliśmy stosując średnią ważoną

c=345,5 ± 5,7[m/s]

Stosując poprzednie wzory liczymy ponownie wykładnik adiabaty.

χ= 1,39±0,05

c)Metoda Quinckego

Prędkość dźwięku obliczymy z wzoru

c= 2 f  h  h 

c =2 | ( h  h )| |f | + | 2f | | h |

f=1001[Hz]

Δh= ±0,5[cm]

Δf = ±5[Hz]

Lp.	c	Δc
1	350,3	11,8
2	340,3	11,7
3	350,3	11,8
4	344,3	11,7
5	346,3	11,7
6	346,3	11,7
7	340,3	11,7
8	344,3	11,7
9	342,3	11,7
10	346,3	11,7
11	344,3	11,7
12	346,3	11,7

Wyniki te uśredniliśmy stosując średnią ważoną

c=345,2 ± 3,4[m/s]

Stosując poprzednie wzory liczymy ponownie wykładnik adiabaty.

χ= 1,39± 0,03

4)Wnioski.

Obliczyliśmy prędkość dźwięku i wykładnik adiabaty trzema metodami i otrzymaliśmy następujące wyniki:

• metoda rezonansowa c=272.5±5,8[m/s] χ=0,87±0,04

• metoda przesunięcia fazowego c=345.5±5,7[m/s] χ= 1,39±0,05

• metoda Quinckego c=345,2±3,4[m/s] χ= 1,39± 0,03

Najbliższe prawdy wyniki otrzymaliśmy metodami przesunięcia fazowego i Quinckego. Niedokładność metody rezonansowej wynika z trudności w znalezieniu kolejnych maksimów ,jest to spowodowane licznymi zakłóceniami.

---