Proste drgania harmoniczne: wahadło matematyczne i fizyczne. Wyznaczanie przyspieszenia ziemskiego i momentu bezwładności.

1. Wiadomości wstępne:

Ruchem harmonicznym prostym nazywamy drgania odbywające się pod wpływem siły F proporcjonalnej do wychylenia x i przeciwnej do niego skierowanej:

F=-kx

Według drugiej zasady dynamiki Newtona: F=ma

ma=-kx

a=d2x/dt2 d2x/dt2+k/m.*x=0

k/m.=2

-częstość kołowa drgań d2x/dt2+2x=0

rozwiązanie ogólne tego równania ma postać

x=Acos( t+)

gdzie A-amplituda drgań , -przesunięcie fazowe, (t+)-faza ruchu

Podstawową cechą ruchu harmonicznego jest jego okresowość. Gdy =0 to x=Acost. Funkcja cosinus jest periodyczna, powtarza się co 2 czyli możemy wyznaczyć okres drgań T

T=2 /

ponieważ k/m.=2

to T=2m/k .

Najprostszymi przykładami ruch harmonicznego prostego są: wahadło matematyczne proste i stożkowe, a także wahadło fizyczne. Ruch wahadła fizycznego można opisać równaniem bryły sztywnej.

2.Wahadło matematyczne proste i stożkowe:

Wahadłem matematycznym prostym nazywamy punkt materialny zawieszony na cienkiej, długiej i nierozciągliwej nici, wykonujący wahania dookoła najniżej położonego punktu zwanego środkiem wahań. Wahadło wprawione w ruch waha się w płaszczyźnie pionowej. Na kulę wahadła działają siły:

G=mg -siła ciężkości skierowana w dół

Fn -siła napięcia nici

Fz=-mgsin -wypadkowa dwóch powyższych sił decydująca o ruchu kulki wahadła

Dla małych wychyleń od pionu(rzędu kilku stopni)można przyjąć, że sin= a w mierze łukowej =x/l. Otrzymujemy wtedy

Fz=-mgx/l

a=-gx/l.

Wzory te mówią, że siła i przyspieszenie w ruchu wahadłowym są proporcjonalne do wychylenia x od środka wahań i stale skierowane ku temu środkowi. Zatem ruch wahadła przy małych kątach wychyleń można traktować jako ruch harmoniczny. Stosujemy zatem wzory:

Fz=md2x/d2

d2x/dt2+gx/l=0 stąd

=g/l stąd

T=2/=l/g

Z tego wynika, że okres drgań nie zależy od amplitudy wahań, nie zależy także od masy wahadła. Oprócz tego wystarczy zmierzyć okres drgań wahadła oraz jego długość aby obliczyć w prosty sposób przyspieszenie Ziemskie ze wzoru:

g=42l/T2 .

Tę samą kulkę możemy wprawić w ruch jednostajny po okręgu w płaszczyźnie poziomej, takie wahadło nazywamy stożkowym. Dokonując rozkładu sił otrzymujemy:

Fr=Gtg

Fr-siła kierująca ruchem wahadła . Skoro dla niewielkich kątów

tgsin to

tg=r/l

Fr=Gr/l=mgr/l

gdzie r promień koła zataczanego przez wahadło. Ponieważ na ciało poruszające się po okręgu działa siła dośrodkowa:

Fz=mV2/r

ponieważ V=2r/T

więc Fr=42mr/T2 .

Porównując dwa wzory na Fr otrzymujemy

mgr/l=42mr/T2

g/l=42/T2

T=2l/g

g=42l/T2

Z tego wynika, że okresy drgań wahadła matematycznego i stożkowego o jednakowych długościach są jednakowe.

3.Wahadło fizyczne:

Wahadło fizyczne jest to bryła sztywna obracająca się dookoła osi nie przechodzącej przez środek ciężkości bryły. Ruch wahadła fizycznego można opisać równaniem bryły sztywnej.

M.=I

gdzie I-moment bezwładności , -przyspieszenie kątowe bryły, M.- moment sił działających bryłę

=d2/dt2

M.=I d2/dt2

Aby ruch bryły był harmoniczny

M.=-D

gdzie D-moment kierujący.

d2/dy2.+D/I*=0

=D/I

=0cos(t+)

=2/T

stąd T=2I/D

jeżeli

D=mgd

to T=2I/mgd.

Z tego wzoru można obliczyć moment bezwładności bryły sztywnej jeśli znamy masę ciała i odległość osi obrotu od środka ciężkości :

I=T2mgd/42 .

Wykonanie ćwiczenia:

Część 1.

Wahadło matematyczne proste i stożkowe.

Numer pomiaru	L [m]	L1 [m]	l [m]	t20 [s]	T [s]	g [m/s2]
1	5,970,01	0,660,01	5,310,01	92,560,01	4,6280,01	9,7870,061
2	5,970,01	0,660,01	5,310,01	92,460,01	4,6230,01	9,8080,061
3	5,970,01	0,660,01	5,310,01	92,340,01	4,6170,01	9,8340,061
4	5,970,01	0,660,01	5,310,01	92,690,01	4,6350,01	9,7570,060

Maksymalny błąd systematyczny pomiaru wyznaczyliśmy za pomocą metody różniczki zupełnej:

, uznając f jako funkcję g.

Otrzymaliśmy następujący wynik:

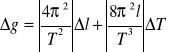
0,06.

Błędów przypadkowych nie bierzemy pod uwagę ze względu na ich stosunkowo niewielką wartość.

Wahadło matematyczne stożkowe.

Nr	Promień okręgu r [m]	Siła dośrodkowa obliczona Fr	Ciężar szalki G1[N]	Ciężar odważników G2[g]	Siła dośrodkowa doświadczalna Frd= G1+ G2	Ciężar kuli G[kg]	t20 [s]	T [s]
1	0,30,001	0,7270,026	0,130,002	0,630,002	0,760,004	1,3040,001	92,280,01	4,610,01
2	0,250,001	0,6050,027	0,130,002	0,53002	0,660,004	1,3040,001	92,280,01	4,610,01
3	0,20,001	0,4840,026	0,130,002	0,380,002	0,510,004	1,3040,001	92,560,01	4,630,01

Maksymalny błąd systematyczny dla siły dośrodkowej doświadczalnej wynosi:

DF
= DG+DG=0,4 [N].

Maksymalny błąd systematyczny siły dośrodkowej obliczonej wynosi:

,

:

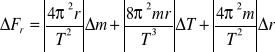
dla: r=0,3 DF=0,000557+0,003152+0,00242=0,026

r=0,25 DF=0,00046+0,00261+0,0242=0,02727.

r=0,20 DF=0,000368+0,00209+0,0242=0,0266

Część II.

Wahadło fizyczne

Rodzaj ciała	m [kg]	rw [cm]	rz [cm]	dw [cm]	dz [cm]	T [s]	DI	Is mierz. kg m2	DIs	Is obliczony kg m2
Pierścień	1,602 0,01	10,4 1	11 1	20,8 1	22,1 1	0,93 0,01	0,00399	0.0184	3,366*10-10	0,0183

Nr pomiaru	1	2	3	4
T50	46,16	46,88	46,34	46,56

I obliczamy za pomocą wzoru:

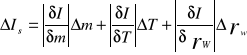
Wnioski

Ponieważ doświadczalna wartość siły dośrodkowej jest równa w granicach błędu obliczonej wartości siły dośrodkowej wnioskujemy, że metoda pomiaru tej siły jak i obliczeń jest dobra. Również przy obliczaniu momentu bezwładności pierścienia wartość wyliczona ma podstawie pomiarów oraz wartość wyliczona ze wzoru są równe w granicach błędu.

Wartość g różni się od wartości tablicowych powodem tego są błędy spowodowane zbyt wielkimi przybliżeniami. Długość nici wahadła była za krótka i za mało było pomiarów aby można było uznać tę metodę pomiaru siły przyciągania Ziemskiego za reprezentacyjną.

Sprawozdanie z ćwiczenia a-4

Justyna Frydrychewicz

3

---