SPIS TREŚCI:
1: 1. Omówić metody interpolacji lokalnej pól skalarnych.
2. Przedstawić ideę kolokacji metodą najmniejszych kwadratów.
2: 3. Metoda M-estymatorów i jej związek z metodą najmniejszych kwadratów.
4. eliminowanie wpływu błędów grubych w metodzie M-estymatorów wg Hubera? Co to są obserwacje dźwigniowe oraz punkt załamania metody?
3: 5. Metody radialnych funkcji bazowych.
6. Twierdzenie o próbkowaniu i jego znaczenie praktyczne.
4: 7. Sieć Swobodna, Wyrównanie wyników pomiarów, Etapy wyrównania sieci swobodnej.
5: 8. Defekt sieci, Metoda pośrednicząca, Klasyfikacja metod odpornych.
6: 9. Całkowanie numeryczne
7: 10. Na czym polega wyrównanie sieci swobodnej metodą najmniejszych kwadratów.1. Omówić metody interpolacji lokalnej pól skalarnych. Wybraną metodę pokazać na przykładzie.
Metody interpolacji lokalnej polegają na tym, że do wyznaczenia wartości w danym punkcie wybieramy punkty z najbliższego otoczenia tego punktu.
Do metod lokalnych zaliczamy:
metodę średniej ważonej- obliczamy wartość prognozowana w danym punkcie na podstawie wzoru:
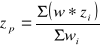
gdzie waga jest odwrotnością odległości (lub kwadratu odległości) między punktem ze znana wartością a punktem interpolowanym ![]()
, k=-1 lub k=-2
metodę najbliższego sąsiada- wartość pomierzona w jednym punkcie przypisywana jest obszarowi wokół tego punktu (metoda najczęściej stosowana w kartografii). Polega na tworzeniu pomiędzy punktami sieci trójkątów (boki łączące 2 punkty dzielimy symetralną; ich przecięcia tworzą mozaikę voronoi). Obszarowi przypisujemy wartość pola skalarnego w tym punkcie.
metodę wielomianu ruchomego- wybieramy punkty z najbliższego otoczenia interpolowanego punktu; następnie obliczamy odległości miedzy tym punktem a pktami o znanej wartości. Aby wykorzystać tę metodę musza być min 4 punkty.
Tworzymy wielomian taki, aby płaszczyzna przechodziła przez interpolowany punkt, np.: z(x,y) = ao + a1x + a2y + a3xy…
Wyznaczamy wartości a:
a = (ATPA)-1 * ATP * w , gdzie w- wartość w punktach powierzonych, P- waga - odwrotność odległości od punktu interpolowanego
Wartości x wyznaczamy na podstawie:
x = ATPA-1 * ATPL
Macierz L- wektor znanych wartości z
metodę elementów skończonych
2. Przedstawić ideę kolokacji metodą najmniejszych kwadratów.
W materiale obserwacyjnym można wyróżnić:
-część regularną (deterministyczną) - trend (x)
-część regularną (stochastyczną) - sygnał (s)
-część nieregularną (stochastyczną) - szum pomiarowy (n)
KOLOKACJA (łac. kolokale = połączenie, kombinacja) - uogólnienie metody najmniejszych kwadratów, w którym uwzględnia się dwa składniki błędu, tzw. szum oraz skorelowany sygnał, który charakteryzuje się przyjętą funkcją korelacji.
Kolokacja łączy w sobie:
-estymację trendu,
-filtrację - oddzielenie szumu pomiarowego,
-predykcję (interpolację) - określenie wartości w punktach, w których nie wykonano pomiaru.
Model kolokacji: L = Ax + (s + n) = Ax + ε, gdzie: Rys…
L - wektor obserwacji
A - prostokątna macierz zawierająca współczynniki
przy niewiadomych
x - wektor niewiadomych (trend)
s - część regularna wektora losowego (sygnał)
n - część nieregularna (szum).
ε = s + n
założenie: s i n są niezależne
Metoda najmniejszych kwadratów polega na minimalizacji sumy kwadratów błędów, dlatego εTP ε -> min, czyli nTCnn-1n + sTCss-1s ->min. Taki warunek trzeba założyć, aby rozwiązać model kolokacji.
W przypadku szczególnym, gdy s = 0 (czyli sygnał jest równy 0), wtedy Css = 0 i Csps = 0.
Mamy wówczas do czynienia z metodą najmniejszych kwadratów: X = (ATCnn-1A)-1ATCnn-1L.
Kolokacja jest więc uogólnieniem metody najmniejszych kwadratów
3. Metoda M-estymatorów i jej związek z metodą najmniejszych kwadratów.
Budowanie modelu odbywa się poprzez wyznaczenie parametrów modelu na podstawie obserwacji. Niektóre z tych obserwacji mogą być obarczone błędami grubymi i wpływać na nieprawidłowe oszacowanie tych parametrów.
Metody odporne są wykorzystywane do eliminowania wpływu obserwacji obarczonych błędami grubymi na szacowane parametry modelu. Jedną z tych metod jest metoda M-estymatorów.
Wyznaczenie parametrów modelu i wyrównanie obserwacji odbywa się tu podobnie jak w metodzie najmniejszych kwadratów, z ta różnicą, że w metodzie najmniejszych kwadratów nie eliminuje się wpływu obserwacji obarczonych błędami grubymi na wyznaczane parametry. W metodzie M-estymatorów odbywa się to poprzez odpowiednie wagowanie tych obserwacji (wprowadza się funkcję wagową). W metodzie najmniejszych kwadratów można ewentualnie wykryć za pomocą testów statystycznych takie obserwacje, a następnie usunąć je ze zbioru danych.
Tok postępowania w metodzie M-estymatorów przebiega podobnie jak w metodzie najmniejszych kwadratów, ale w przeciwieństwie do tej drugiej przebiega iteracyjnie. Kolejne iteracje przebiegają jak wyznaczanie parametrów modelu i wyrównanie obserwacji w metodzie pośredniczącej ,ale w każdej kolejnej iteracji tworzy się nową macierz wag, w której wagi obserwacji obarczonych błędami grubymi są coraz mniejsze.
Przebieg obliczeń w metodzie M-estymatorów jest następujący:
1.Pierwsze wyznaczenie parametrów modelu : ![]()
2.Wyznaczenie poprawek v obserwacji: ![]()
k- nr iteracji
3.Obliczenie funkcji wagowej w: w(k)=diag (w1(k) w2(k) ... wn(k) )
4.Kolejne wyznaczenie parametrów x: ![]()
5.Wyznaczenie różnicy między wektorami parametrów wyznaczonymi w 2-ch kolejnych iteracjach:
ε=x(k+1)-x(k)
Proces iteracyjny kończy się ,gdy ε osiągnie dopuszczalną wartość.
4. W jaki sposób eliminowany jest praktycznie wpływ błędów grubych w metodzie M-estymatorów wg Hubera? Co to są obserwacje dźwigniowe oraz punkt załamania metody?
Praktyczny sposób eliminowania błędów grubych według Hubera.
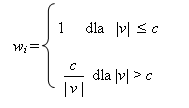
Należy przeprowadzić test Hubera dla funkcji wagowej:
gdzie:
wi - waga obserwacji
v - poprawki obserwacji
k - dobrany współczynnik k > 0
mv - błąd poprawki,
c = k mv
Oznacza to, że dla wartości poprawek, które się mieszczą w przedziale poprawek wagi mają wartości 1, poprawki, które nie leżą w tym przedziale, traktowane są jako błędy grube. Modyfikacja układu nadaje mniejsze wagi. Im mniejsza waga, tym mniejszy wpływ obserwacji na wynik końcowy.
Obserwacje dźwigniowe
Są to obserwacje, które leżą daleko od środka ciężkości pozostałych obserwacji (od geometrycznie uporządkowanych stałych punktów). Występujące w tych obserwacjach błędy grube są szczególnie niebezpieczne. Punkty dźwigniowe można określić na podstawie analizy geometrii. Można zaplanować obserwacje tak, żeby obserwacje dźwigniowe wykonać z większą dokładnością lub zwiększyć ich ilość.
Obserwacja jest obserwacją dźwigniową, jeśli wartość hii w macierzy projekcji jest duża, tzn. większa od wartości średniej hśr = ![]()
, gdzie m - liczba wyznaczanych parametrów, n - liczba obserwacji. Oznacza to, że duże obserwacje mają większą wartość od wartości średniej hii> hśr
Macierz projekcji H = A(ATA)-1AT opisuje geometrie macierzy
Punkt załamania metody
Jest to procentowy udział obserwacji obarczonych błędem grubym, przy których metoda oporna daje poprawne wyniki. Może wystąpić w przypadku występowania ukrytych obserwacji dźwigniowych, wówczas błędy grube nie są wykrywalne i dochodzi do załamania metody.
5. Metody radialnych funkcji bazowych.
Metoda radialnych funkcji bazowych należy do globalnych metod interpolacyjnych (funkcję interpolacyjną buduje się tu w oparciu o cały obszar danych).
Wartość w punkcie interpolowanym (mając jego współrzędne x i y) w tej metodzie wyznacza się wg następującego wzoru:
![]()
.
αi,βi-nieznane parametry
R( ri ( x, y))-radialne funkcje wagowe (zależą od odległości poziomej -w płaszczyźnie x ,y -r).
ri2=(x-xi)2+(y-yi)2
xi,yi -współrzędne punktu i pomiarowego, w którym zmierzono wartość zi
Pj (x,y)- wielomian rzędu k
Jednym z przykładów radialnych funkcji bazowych jest spline minimalnej krzywizny, dla którego radialna funkcja bazowa ma postać:
R=ri2ln( ri2),
a wielomian Pj: ν00 +ν10x +ν01y.
Wzór na wartość interpolowaną w punkcie o współrzędnych x,y ma postać:
* ![]()
,
gdzie λi ,νij -nieznane parametry( n+3 niewiadome),
n- liczba punktów pomiarowych
Równania powyższej postaci układamy dla każdego i-tego punktu pomiarowego .
Do tak utworzonego układu równań dodajemy 3 równania:
![]()
![]()
![]()
W oparciu o n równań * i 3 powyższe równania wyznaczamy parametry λi ,νij.
Po ich wyznaczaniu możliwe będzie wyznaczenie w dowolnym punkcie o współrzędnych x, y wartości z, w oparciu o wzór *.
6. Twierdzenie o próbkowaniu i jego znaczenie praktyczne.
Twierdzenie o próbkowaniu daje odpowiedź, w których miejscach profilu terenu należy pomierzyć punkty, przy założeniu, że profil terenu odpowiada sygnałowi i że pomiar odbywa się z określonym interwałem ΔX. Jest to dyskretyzowanie z interwału ΔX, mierzone w postaci dyskretnych punktów. Musimy dobrać taki interwał, aby był mniejszy od połowy długości fali w sygnale:
ΔX≤![]()
= ![]()
= ![]()
;
gdzie:
ΔX - próbkowanie
fmax - max częstotliwość,
ωg -częstotliwość graficzna,
ω = 2пf -częstotliwość kołowa
lmin -minimalna długość fali
Oznacza to, że na jedną próbkę (ΔX) pomierzone są dwie wartości.
Jeśli konkretna wartość jest zawarta w próbkowaniu, to możemy odtworzyć zawarte informacje uwidocznione po analizie spektralnej. Czyli analiza spektralna to przeniesienie problemu do innych dziedzin, np. pomiar w współrzędnych xy (dziedzina w przestrzeni euklidesowej) w sygnał rejestrowany w czasie (przejście w dziedzinę częstotliwości).
Jest to fundamentalne twierdzenie o przetwarzaniu sygnału, zawarta jest kompletna informacja o danym sygnale (analiza spektralna)
7. Sieć Swobodna, Wyrównanie wyników pomiarów, Etapy wyrównania sieci swobodnej.
Sieć swobodna to sieć geodezyjna, która nie posiada zdefiniowanego układu odniesienia. Inaczej jest to sieć o niezerowym defekcie zewnętrznym (defekt układu odniesienia).
Sieć swobodna - sieć posiadająca defekt sieci wynikający z układu nawiązania (brak dostatecznego nawiązania do układu zewnętrznego) d= m - R(A) > 0.
Sieć swobodna jest to sieć niezależna, która ma ustalone powiązanie z układem odniesienia poprzez powstanie ogólnego warunku VTPV+XTX= min. Sieć ta wyróżnia się dodatkowym spośród wszystkich możliwych warunków sieci niezależnych ma najmniejszą sumę kwadratów błędów średnich wyznaczanych parametrów. Suma poszczególnych parametrów powinna być równa 0. Sieć swobodna występuje wtedy, gdy nie jest zdefiniowany układ odniesienia.
Wyrównanie wyników pomiarów polega na wyznaczeniu estymatorów wartości prawdziwej mierzonej wielkości. W przypadku, gdy odchylenie standardowe nie jest znane, należy również wyznaczyć estymator tego parametru. Aby móc wyrównać sieć i uzyskać współrzędne w określonym układzie należy usunąć defekt sieci tzn. doprowadzić do takiego stanu, aby r=k, rząd macierzy A był równy liczbie niewiadomych pośredniczących.
Sieć swobodna niedowiązywana do układu odniesienia nie ma punktów stałych.
Wyrównanie sieci swobodnej:
Podejście pragmatyczne - dopisanie równań pseudoobserwacji B do macierzy A i nadanie im dużych wag;
Podejście ścisłe:
gdy macierz N jest nieosobliwa det(N)<>0
gdy macierz N jest osobliwa det(N)=0
odwrócenie całej macierzy blokowej i wyciągnięcie interesującego nas elementu
=
korzystanie z odwrotności uogólnionej macierzy (a w naszym szczególnym przypadku z pseudoodwrotności)
- odwrotność uogólniona
- pseudoodwrotność
Sieć swobodną wyrównuje się poprzez nałożenie na wyrównywane parametry odpowiednich warunków:
dla sieci niwelacyjnej (występuje maksymalnie jeden defekt, więc warunek tylko jeden)
nakłada się warunek na przesunięcie w kierunku H
dla sieci poziomej (maksymalnie 4 defekty, więc mogą być 4 warunki)
warunek na przesunięcie w kierunku X, Y
warunek na obrót w płaszczyźnie XY
warunek na skalę
dla sieci przestrzennej (maksymalnie 7 defektów, więc może być 7 warunków)
warunek na przesunięcie w kierunku X, Y, Z
warunek na obrót wokół osi X, Y, Z
warunek na skalę
Etapy wyrównania sieci swobodnej:
Mając dane współrzędne pkt, odległości, błędy odległości, kąty:
Obliczamy współrzędne przybliżone, obserwacje przybliżone
Układamy równania poprawek dla długości i kątów
Ogólny układ obserwacyjny V=Ax-L
Macierz kowariancji pierwotnych obserwacji „C”
Układamy ostateczną macierz wag P=C(-1), ATPA
Nakładamy warunki (na wysokość)
Układamy macierz Kofaktorów „Q”
Rozwiązujemy układ z charakterystyką dokładności dx=QATPL, V=Adx-L
Obliczamy defekt sieci
Błędy niewiadomych
Wyrównujemy współrzędne, odległości, kąty
Błędy poprawek
Ocena dokładności wyrównania - test lokalny
8. Defekt sieci, Metoda pośrednicząca, Klasyfikacja metod odpornych.
Defekt zewnętrzny występuje w sieciach jedno dwu i trójwymiarowych. W sieci jednowymiarowej (sieci niwelacyjnej) maksymalnie możliwy defekt to 1 spowodowany możliwym przesunięciem sieci w kierunku Z lub H. W sieci dwuwymiarowej max defekt to 4 a są to: przesunięcie w kierunku X lub Y, obrót w płaszczyźnie XY oraz defekt skali. W sieci trójwymiarowej max defekt to 7: przesunięcie w kierunku X po Y i po Z rotacja czyli obrót wokół osi X, Y, Z oraz defekt skali. Może także występować defekt wewnętrzny czyli tzw konfiguracja spowodowana brakiem obserwacji niezbędnych do uzyskania wyznaczalności wzajemniego położenia punktów sieci.
d=M-R(A); gdzie M- liczba niewiadomych
dx, dy - poprawki do współrzędnych wyrównanych
Warunek dot. przesunięcia w kierunku X i Y:
![]()
m- liczba obserwacji
Warunek dla obrotu w płaszczyźnie XY:
![]()
![]()
Warunek skali:
![]()
Warunek dla sieci poziomej:
![]()
Metoda pośrednicząca z warunkami na niewiadome - polega na bezpośrednim wykorzystaniu związków zachodzących w tej sieci między wielkościami podlegającymi pomiarowi. Formułuje się układ wzajemnie niezależnych równań. Równań tych (warunkowych) tworzy się tyle ile jest obserwacji nadliczbowych ɣ= n-v+d gdzie n- liczba obserwacji, v-liczba wspólnych punktów niewiadomych. Układamy warunki: Ax= L+v VTPV= min BT*x= w gdzie B- macierz współczynników przy poprawkach, w- wektor wyrazów wolnych, w sieci swobodnej w=0. Wprowadzając przyporządkowanie każdemu z równań warunkowych mnożników Legangrea uzyskujemy Ω= VTPV+2kT(Bx-w) = min. Niewiadome to wektor x i k gdzie k- mnożnik Legangrea.
Klasyfikacja metod odpornych:
1) Estymacja parametrów:
a) pasywne
- met najmniejszych kwadratów
- met statystyczne
b) aktywne
- LMS - estymatory
- M - estymatory
2) Inne
- odporne, aktywne, f.sklejane
- odporne, predukcja liniowa
9. CAŁKOWANIE NUMERYCZNE
Całkowanie numeryczne - polegająca na przybliżonym obliczaniu całek oznaczonych.
Proste metody całkowania numerycznego polegają na przybliżeniu całki za pomocą odpowiedniej sumy ważonej wartości całkowanej funkcji w kilku punktach. Aby uzyskać dokładniejsze przybliżenie dzieli się przedział całkowania na niewielkie fragmenty. Ostateczny wynik jest sumą oszacowań całek w poszczególnych podprzedziałach. Najczęściej przedział dzieli się na równe podprzedziały.
Do całkowania numerycznego najważniejsze jest gdy mamy wynik funkcji dążymy do rozwiązania równania, lub możemy zastosować dowolnie inna funkcję.
Metoda prostokątów
Wzór na metode punktu środkowego
Jeśli funkcja f(x) zmienia się w niewielkim stopniu na przedziale (x * ,x * + h), reguła taka da dobre przybliżenie całki.
Metoda trapezów jeśli chodzi o trapezy to połowa odcinka podstawy dzielimy na połowę
Metoda trapezów polega na tym, że figurę ABCD zastępujemy figurą złożoną z trapezów wpisanych, tzn. krzywą aproksymujemy linią łamaną w nią wpisaną. Przedział całkowania (a,b) dzielimy przy tym na n równych części o długościach:
.
Wzór przybliżony w metodzie trapezów:
Metoda daje zazwyczaj lepsze przybliżenie niż metoda prostokątów, ale wymaga obliczenia wartości funkcji w 2 punktach.
Metoda parabol (Simpsona)
Wymaga podzielenia przedziału całkowania na parzystą liczbę podprzedziałów, tzn.
dla uproszczenia oznaczamy:
xi = a + ih oraz fi = f(xi)
wykonując całkowanie wielomianu interpolacyjnego Lagrange'a z 3 kolejnych punktów otrzymujemy wzór Simpsona:
10. Na czym polega wyrównanie sieci swobodnej metodą najmniejszych kwadratów.
Zasada stosowania metody najmniejszych kwadratów opiera się na następujących założeniach:
wynik pomiaru Li = xi można uważać za sumę wartości prawdziwej Lp = a oraz błędu εi
![]()
należy dobrać takie wielkości
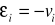
, aby suma kwadratów błędów była najmniejsza
![]()
Sieć swobodną wyrównuje się poprzez nałożenie na wyrównywane parametry odpowiednich warunków:
dla sieci niwelacyjnej (występuje maksymalnie jeden defekt, więc warunek tylko jeden)
nakłada się warunek na przesunięcie w kierunku H
dla sieci poziomej (maksymalnie 4 defekty, więc mogą być 4 warunki)
warunek na przesunięcie w kierunku X, Y
warunek na obrót w płaszczyźnie XY
warunek na skalę
dla sieci przestrzennej (maksymalnie 7 defektów, więc może być 7 warunków)
warunek na przesunięcie w kierunku X, Y, Z
![]()
warunek na obrót wokół osi X, Y, Z
warunek na skalę
Warunki te wprowadza się w macierzy B
BT - macierz współczynników przy wyznaczanych parametrach
x - wektor wyznaczanych parametrów
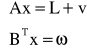
Równania warunkowe dopisuje się do równań obserwacji
A - macierz współczynników przy niewiadomych
L - macierz wyrazów wolnych
v - poprawki
W ten sposób otrzymujemy rozszerzony układ równań normalnych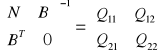
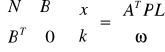
N = ATPA,
k - korelaty
det(N) ≠ 0
![]()
- wyrównane parametry
Jeżeli det(N) = 0, wówczas należy wykonać rozkład spektralny macierzy N na wektory i wartości własne
G - macierz zawierająca wektory własne (tworzy się ją korzystając z przybliżonych współrzędnych)
Po utworzeniu macierzy G możemy obliczyć wartość Q11
![]()
Jeśli mamy macierz Q11 możemy obliczyć wyrównane parametry z powyższego wzoru na ![]()
Po obliczeniu wyrównanych parametrów przeprowadza się analizę dokładności i oblicza się:
poprawki (v)
![]()
, ![]()
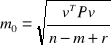
błąd typowego spostrzeżenia (m0)
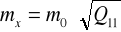
błędy współrzędnych
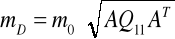
błędy obserwacji
![]()
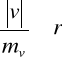
błędy poprawek
Na koniec przeprowadza się test lokalny: ,r = 2 lub r = 3
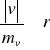
![]()
![]()
![]()
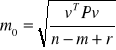
![]()
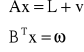
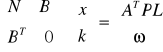
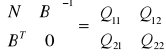
Wyszukiwarka
Podobne podstrony:
zagadnienia zmoo, Pytanka na Borkowskiego, Metody opracowania geodanych
instytucje UE, zagadnienia, skrypt, INSTYTUCJE OPRACOWANE ZAGADNIENIA, INTEGRACJA EUROPEJSKA - PYTAN
Kilka zagadnień omówionych w krótkim opracowaniu, Prawo, Prawo2
zagadniena na botanike z opracowaniem
Zagadnienia do samodzielnego opracowania
Zagadnienia do koła opracowane finanse
Zagadnienia na kolokwium opracowanie
Ch F Hockett Zagadnienie uniwersaliów w języku [opracowanie]
ETYKA zagadnienia do samodzielnego opracowania
Zagadnienia egzamin pedagogika opracowane
zagadnienia do egzaminu opracowane ostateczne
Zagadnienia kultury współczesnej - opracowanie, zagadnienia kultury współczesnej
ZAGADNIENIA DO EGZAMINU opracowanie, Pedagogika
Zagadnienia do kolokwium opracowanie psychologia ogólna, Pedagogika 1 rok !
opracowanie zagadnień na egzamin, opracowanie pytań egzaminacyjnych
Zagadnienia z socjologii organizacji opracowanie, sum administracja, I rok, Socjologia organizacji
Zagadnienia do egz. -opracowane, UCZELNIA
Zagadnienia na filozofię i opracowanie, Filozofia
więcej podobnych podstron