CIĄGI FUNKCYJNE
DEF 1.Ciąg, którego wyrazami są funkcje f1, f2, f3,f4,.....określone w pewnym zbiorze E, nazywamy ciągiem funkcyjnym i oznaczamy symbolem (fn),lub zapisujemy wzorem fn(x) , n∈N i x ∈E.
Przykład 1.
Niech ![]()
,![]()
, wtedy początkowe elementy tego ciągu są następujące:
![]()
,
![]()
,
![]()
, .... (rysunek 10.2.1).
UWAGA 1. Jeśli w ciągu funkcyjnym ustalimy x, to otrzymamy ciąg liczbowy. Ciąg ten może być dla pewnej wartości x zbieżny a dla innych rozbieżny.
DEF 2. Funkcję f określona w zbiorze E wzorem ![]()
nazywamy funkcją graniczną lub granicą ciągu funkcyjnego (fn ),jeżeli tylko ciąg ten jest zbieżny dla każdego x∈E i mówimy, że ciąg funkcyjny (fn ) jest zbieżny w zbiorze E do funkcji f.
Przykład 2.Wyznacz funkcję graniczną ciągu funkcyjnego ![]()
Początkowe elementy tego ciągu są następujące:
![]()
,![]()
,![]()
,![]()
,..............
Ciągu funkcyjnego fn możemy przedstawić jako fn (x)=a nbn, gdzie a n=![]()
b n=![]()
. Zauważmy, że a n jest ciągiem malejącym do zera zaś b n jest ograniczony wobec tego ![]()
.Czyli funkcja graniczna f(x)=0.
DEF 3. Mówimy, że ciąg funkcyjny ![]()
jest ciągiem punktowo zbieżnym do funkcji f, co zapisujemy symbolicznie ![]()
, jeżeli spełniony jest poniższy warunek:
![]()
.
UWAGA 2. Zbieżność punktowa ciągu funkcyjnego wystarcza do tego aby istniała funkcja graniczna ale jest za słaba aby na to aby na podstawie własności wyrazów ciągu funkcyjnego można było określić własności funkcji granicznej.
DEF 4. Mówimy, że ciąg funkcyjny ![]()
jest ciągiem jednostajnie zbieżnym do funkcji f, co zapisujemy symbolicznie ![]()
, jeżeli spełniony jest poniższy warunek:
![]()
.
UWAGA 3. Proszę zwrócić uwagę, że różnica pomiędzy DEF 3 i DEF 4 jest pozornie niewielka, ponieważ zamieniono miejscami kwantyfikatory ( w DEF 3 kwantyfikator ![]()
jest na początku, a w DEF 4 na końcu wszystkich kwantyfikatorów).
Tak naprawdę pokażemy na podstawie przykładów, że jest to różnica istotna.
Przykład 3.Punktową zbieżność ciągu funkcyjnego można zinterpretować tak:
dla każdej liczby ![]()
ciąg funkcyjny ![]()
staje się ciągiem liczbowym, który może mieć jakąś granicę np.: ![]()
. Wtedy funkcja dana wzorem ![]()
jest granicą punktową ciągu ![]()
. Weźmy na przykład ciąg funkcyjny ![]()
dany wzorem ![]()
.Początkowe elementy tego ciągu są takie: ![]()
.Dla każdej ustalonej liczby ![]()
ciąg liczbowy ![]()
jest zbieżny do zera, więc ciąg liczbowy ![]()
, bo funkcja sinus jest funkcją ciągłą i ![]()
, więc zgodnie z naszą interpretacją funkcja zerowa ![]()
jest granicą punktową powyższego ciągu (rysunek 10.2.2). Na poniższym rysunku kolejne elementy ciągu „wydłużają się” ( zwiększają swój okres), ale zawsze „dotykają” prostych równoległych do osi OX przechodzących przez liczby -1 i 1.
Jednostajna zbieżność oznacza, że w każdym otoczeniu wykresu funkcji granicznej f leży nieskończenie wiele wykresów elementów ciągu funkcyjnego poza pewną skończoną ich ilością. Zgodnie z tą interpretacją zbieżności jednostajnej powyższy ciąg funkcyjny ![]()
jest zbieżny punktowo do funkcji ![]()
, ale nie jest do niej zbieżny jednostajnie, ponieważ w pasie np.: dla ![]()
nie leży żaden wykres jakiegokolwiek elementu ciągu. (rysunek 10.2.3).
Przykład 4 Rozpatrzmy ciąg funkcyjny ![]()
![]()
. Początkowe wyrazy tego ciągu są następujące: ![]()
, ![]()
, ![]()
,....
Pokażemy, że jest to ciąg funkcyjny zbieżny jednostajnie do funkcji danej wzorem ![]()
.
Mamy ![]()
, ponieważ funkcja sinus jest ograniczona z góry przez 1 i z dołu przez -1. Proszę zwrócić uwagę, że bez względu na wybór liczby x ciąg ![]()
ma zawsze tą samą liczbę ![]()
, taką jak ciąg liczbowy![]()
.
Jak widać na rysunku 10.2.4 kolejne elementy ciągu zbliżają się do funkcji granicznej oznaczonej kolorem czerwonym.
Twierdzenie 1.Jeśli ciąg funkcyjny ![]()
jest w przedziale E jednostajnie zbieżnym do funkcji granicznej f i wszystkie funkcje ![]()
są ciągłe w pewnym punkcie x0 przedziału E, to funkcja graniczna f jest ciągła w tym punkcie.
Przykład 5.Weźmy ciąg funkcyjny ![]()
![]()
. Dla każdej liczby ![]()
ciąg liczbowy ![]()
, natomiast dla ![]()
![]()
, więc jedynym kandydatem na funkcję graniczną jest funkcja ![]()
dana wzorem 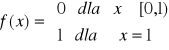
(rysunek 10.2.5).
Jak widać na rysunku funkcja graniczna nie jest ciągła w punkcie x=1, więc zbieżność rozpatrywana w tym przykładzie zgodnie z Twierdzeniem 1 nie może być jednostajna ( wszystkie elementy tego ciągu są oczywiście funkcjami ciągłymi).
Twierdzenie 2.Jeżeli w przedziale E
10 funkcje ![]()
mają ciągłe pochodne (są klasy C1)
20 ciąg (![]()
) jest jednostajnie zbieżnym do pewnej funkcji f
30 ciąg (![]()
) jest jednostajnie zbieżnym do pewnej funkcji p
to funkcja f jest w przedziale E klasy C1 i zachodzi równość
![]()
Twierdzenie 3. Jeśli ciąg funkcyjny (![]()
) jest w przedziale <a, b> jednostajnie zbieżnym do funkcji f i wszystkie funkcje ![]()
są całkowalne w tym przedziale, to funkcja f jest całkowalna w tym przedziale i zachodzi równość
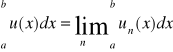
ZADANIA
1.Wyznacz funkcje graniczne ciągów funkcyjnych
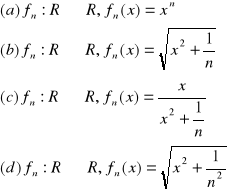
Wyszukiwarka
Podobne podstrony:
ciagi funkcyjne
ściąga Ciągi funkcyjne
ciagi geometryczne, Matematyka, Matematyka(3)
Ciągi funkcyjne
Zadania Ciągi liczbowe Politechnika Poznańska PP, Automatyka i Robotyka, Analiza matematyczna
matematyka ciągi
matematyka 2 podrecznik dla liceum i technikum zakres rozszerzony rozdzial 5 ciagi pdf
Analiza matematyczna Wykłady, CIAGI LICZBOWE
Wardach I - Matematyka podstawowa 07, ciagi
24 ciagi i szeregi funkcyjne 6 3 szeregi fouriera
3 Indukcja matematyczna, ciągi granice
22 ciagi i szeregi funkcyjne 6 1 ogolne wlasnosci ciagow i szeregow funkcyjnych
Ciągi liczbowe - ćwiczenia, Analiza matematyczna
zagadnienia, punkt 12, XII Ciągi i szeregi funkcyjne - zbieżność punktowa i jednostajna
matematyka ciagi
Ciągi- wzory warunki, Do Matury, Matematyka
więcej podobnych podstron