XI. Równowaga chemiczna
XI.1. Reakcje nieodwracalne
W chemii i technologii chemicznej znamy przykłady reakcji, które zachodzą praktycznie ilościowo, lub innymi słowy zachodzą ze stuprocentową wydajnością. Dzieje się tak, gdy jeden z produktów opuszcza środowisko reakcji, w którym ona zachodzi. Mówiąc dokładniej reakcje chemiczne zachodzą
w różnych układach reakcyjnych, które
w praktyce mogą mieć charakter otwarty lub zamknięty. Układy otwarte wymieniają masę
i energię z otoczeniem. Układy zamknięte nie wymieniają masy z otoczeniem, natomiast są zdolne do wymiany energii, głównie energii cieplnej.
Przykładem układu otwartego może być silnik spalinowy, chłodzony powietrzem lub wodą, pobierający z atmosfery powietrze i wydalający do niej spaliny (CO2, para wodna), w którym reakcje spalania benzyny lub oleju napędowego mają charakter nieodwracalny. Kolejny przykład, to roztwarzanie nieszlachetnego metalu, np. granulki cynku, w otwartej probówce lub zlewce z roztworem kwasu.
Zn + 2H+ = Zn2+ + H2↑
Reakcja ta jest egzotermiczna, dlatego jej ciepło jest oddawane do otoczenia, a wypierany wodór ulatnia się do atmosfery.
Charakter nieodwracalny mają reakcje samorzutnego rozkładu nietrwałych substancji chemicznych, np. nadtlenku wodoru w otwartym naczyniu. Nieodwracalny charakter mogą mieć endotermiczne reakcje rozkładu termicznego substancji trwałych, w wyniku czego powstają trwałe, lecz aktywne chemicznie produkty. W praktyce przemysłowej, metodą prażenia wapienia (naturalny CaCO3) uzyskuje się na dużą skalę wapno palone (CaO), jako produkt o dużym znaczeniu gospodarczym:
CaCO3 → CaO + CO2↑
Reakcjami nieodwracalnymi są reakcje spalania węgla i węglowodorów, reakcje zobojętniania mocnych kwasów mocnymi zasadami, reakcje utleniania pierwiastków o dużym powinowactwie chemicznym do tlenu.
XI.2. Reakcje odwracalne. Równowaga dynamiczna
W wielu przypadkach stwierdzamy, że reakcje chemiczne w układzie zamkniętym nie przebiegają do końca, ponieważ mają charakter odwracalny. Odwracalność reakcji chemicznej polega na tym, że w początkowym okresie zmieszane substraty reagują ze sobą z dużą szybkością, ale jednocześnie powstające produkty wchodzą w reakcję odwrotną
i odtwarzają substraty. W miarę upływu czasu, spadek stężeń substratów powoduje zmniejszenie szybkości reakcji tworzenia produktów, których stężenia wzrastają i tym samym zwiększają szybkość reakcji odwrotnej.
Gdy szybkości obydwu reakcji zrównają się, to
w danym układzie reakcyjnym ustala się między substratami i produktami stan równowagi. Makroskopowo w tym układzie nic się nie zmienia, ponieważ w stałej temperaturze i pod stałym ciśnieniem stężenia wszystkich reagentów są ustalone i mimo upływu czasu nie zmieniają się. Formalnie, przez analogię do sytuacji przedstawionej na rys. 1, stan równowagi między substratami i produktami
w układzie reakcyjnym moglibyśmy uznać za statyczny.
Rys.1. Przykład równowagi statycznej
Huśtawka jest podparta w środku ciężkości, a dziewczęta, obydwie o takiej samej masie, siedzą w tej samej odległości od punktu podparcia. Równomiernie obciążona huśtawka pozostaje w bezruchu.
Jednak w skali mikro cząsteczki reagentów
w układzie reakcyjnym nie pozostają w bezruchu, dochodzi do wzajemnych zderzeń cząsteczek, które mogą być zderzeniami efektywnymi. Oznacza to, że
w stanie równowagi w układzie zachodzą równocześnie reakcje tworzenia produktów i odtwarzania substratów. Ponieważ szybkości tych reakcji są takie same, to masa powstałych w danym momencie produktów jest równa masie odtworzonych w tym samym momencie substratów.
Stan równowagi w zamkniętym układzie reakcyjnym, przez analogię do sytuacji przedstawionej na rys. 2, ma charakter dynamiczny.
Rys. 2. Przykład równowagi dynamicznej
Do naczynia wpływa tyle samo wody ile z niego równocześnie wypływa.
Mimo dynamicznego przepływu wysokość słupa wody w naczyniu utrzymuje się na stałym poziomie.
Uwaga: Fakt, że reakcja chemiczna jest odwracalna odnotowujemy w równaniu stechiometrycznym
i zamiast znaku równości między jego lewą i prawą stroną wstawiamy dwie przeciwnie skierowane strzałki.![]()
W tekstach edytowanych komputerowo stosuje się znak ↔ .
W dalszych rozważaniach rozpatrzymy endotermiczną reakcję w fazie gazowej
CO2(g) + H2(g) ↔ CO(g) + H2O(g), ΔH = 40,3 kJ/mol,
która zachodzi w stałej temperaturze w reaktorze
o objętości V.
Warunki: V = const, T = const.
Szybkość reakcji tworzenia produktów:
v→ = k1 ⋅ cCO2 ⋅ cH2 v→ maleje
Szybkość odtwarzania substratów:
v← = k2 ⋅ cCO ⋅ cH2O v← rośnie
Czas
W stanie równowagi: v→ = v← ,
stąd
k1 ⋅ cCO2 ⋅ cH2 = k2 ⋅ cCO ⋅ cH2O
Iloraz stałych szybkości k2/k1 ma wartość stałą, równą Kc:, określaną mianem stężeniowej stałej równowagi reakcji chemicznej. W rozpatrywanym przykładzie stała równowagi Kc jest dana wzorem:
![]()
w którym stężenia molowe cX reagentów w stanie równowagi są podzielone przez jednostkowe stężenie standardowe, co = 1 mol/m3 lub 1 kmol/m3.
Zatem cx/co = [X] są bezwymiarowymi wartościami stężeń reagentów w stanie równowagi.
Stężeniowa stała równowagi reakcji chemicznej
w fazie gazowej jest wielkością bezwymiarową, zależną tylko od temperatury w zamkniętym układzie reakcyjnym.
XI.3. Prawo działania mas
Przedstawione wyżej rozważania doprowadziły nas do prawa działania mas, sformułowanego
w latach 1864-1867 przez norweskich chemików Cato Guldgerga i Petera Waagego.
Cato Maximilian Guldberg (1836-1902) i Peter Waage (1833-1900)
na zdjęciu z ich autografami
Prawo działania mas W reakcji odwracalnej substancje reagują tak długo, dopóki stosunek iloczynu równowagowych stężeń produktów do iloczynu równowagowych stężeń substratów nie osiągnie pewnej stałej wartości, charakterystycznej dla danej reakcji i dla danej temperatury. |
W ogólnym przypadku równanie stechiometryczne reakcji odwracalnej ma postać
aA + bB + … ↔ qQ + rR + …,
a stężeniowa stała równowagi tej reakcji dana jest wzorem:
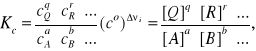
gdzie wykładniki potęg równowagowych stężeń reagentów są równe odpowiednim współczynnikom stechiometrycznym νi, zaś Δνi = (Σνi,substraty - Σνi,produkty)
Stan równowagi w reakcjach w fazie gazowej można ilościowo określić za pomocą równowagowych ciśnień parcjalnych pi (cząstkowych) reagentów
i ciśnieniowej stałej równowagi Kp lub równowagowych ułamków molowych reagentów i słałej równowagi Kx. Podobnie jak stężeniowa równowagi, stała Kp jest wielkością bezwymiarową, dlatego ciśnienia parcjalne poszczególnych reagentów są podzielone przez ciśnienie standardowe: po = 1,01325·105 Pa = 101,325 kPa.
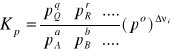
Stała równowagi Kx wyrażona przez ułamki molowe reagentów jest z definicji wielkością bezwymiarową.
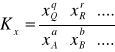
Wszystkie te stałe są sobie równe tylko wtedy, gdy dla danej reakcji Δνi ≡ 0, tzn. wówczas, gdy suma współczynników stechiometrycznych substratów jest równa sumie współczynników stechiometrycznych produktów. Jako typowe przykłady można wymienić następujące reakcje w fazie gazowej:
H2 + I2 ↔ 2HI
CO + H2O ↔ CO2 + H2
CH4 + Br2 ↔ CH3Br + HBr
Dla wielu celów praktycznych konieczna jest znajomość wzajemnej zależności między stałymi Kc i Kp. Aby tę zależność wyznaczyć skorzystamy z prawa Daltona, które mówi, że całkowite ciśnienie (pc)
w układzie zamkniętym jest sumą ciśnień parcjalnych składników w mieszaninie gazów:
pc = p1 + p2 + p3 + … + pk = Σpi
Ułamek molowy i-tego składnika mieszaniny gazowej jest równy:
xi = pi/pc
pi = xi·pc
Na podstawie równania stanu gazu doskonałego możemy dla i-tego składnika napisać:
piV = niRT
pi = (ni/V)RT = ciRT
ci = pi/RT
gdzie ni jest licznością, a ci stężeniem i-tego składnika
w mieszaninie gazów o objętości V w temperaturze T,
zaś R jest uniwersalną stałą gazową.
Po podstawieniu stosunku ci = pi/RT do wyrażenia na Kc otrzymujemy ogólny wzór:
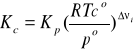
XI.4. Zastosowania prawa działania mas
Stała równowagi reakcji odwrotnej
Reakcja syntezy pentachlorku fosforu w fazie gazowej jest egzotermiczną reakcją odwracalną:
PCl3(g) + Cl2(g) ↔ PCl5(g), ΔH = - 125,5 kJ/mol,
![]()
Reakcja jest odwracalna, więc można ją zapisać
w odwrotnym kierunku.
PCl5(g) ↔ PCl3(g) + Cl2(g), ΔH = 125,5 kJ/mol,
![]()
Wniosek: Stała równowagi reakcji odwrotnej jest odwrotnością stałej równowagi reakcji wyjściowej.
Związek stałej Kp z ciśnieniem całkowitym mieszaniny reakcyjnej
Obecnie spróbujemy wyznaczyć ciśnieniową stałą równowagi dla reakcji syntezy pentachlorku fosforu znając równowagowe ułamki molowe PCl3, Cl2 i PCl5
i całkowite ciśnienie mieszaniny reakcyjnej w układzie. Na podstawie wcześniejszych rozważań mamy:
pPCl3 = xPCl3·pc
pCl2 = xCl2· pc
pPC5 = xPCl5·pc
Δνi = 1-2 = -1
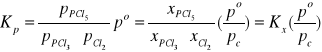
Reakcje z udziałem fazy stałej i fazy gazowej
w układzie zamkniętym
Jako pierwszy przykład rozpatrzymy reakcję redukcji węglem ditlenku węgla do tlenku węgla (reakcja Boudouarda):
CO2(g) + C(s) ↔ 2CO(g)
Korzystając z wyrażenia na Kx możemy napisać:
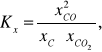
ale węgiel nie jest składnikiem fazy gazowej, a jego ułamek molowy, jako chemicznie czystej fazy stałej jest z definicji równy 1. Ostatecznie, stała równowagi Kx reakcji Boudouarda dana jest wzorem:
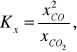
w którym występują ułamki molowe CO i CO2, przy czym ich suma jest równa 1. Z samych względów, węgiel, jako faza stała nie występuje w wyrażeniach na stężeniową i ciśnieniową stałą równowagi tej reakcji.
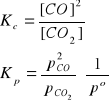
Kolejnym przykładem jest reakcja termicznego rozkładu (dysocjacji termicznej) stałego węglanu amonu.
(NH4)2CO3(s) ↔ NH3(g) + CO2(g) + H2O(g)
Stałe równowagi tej reakcji dane są wzorami:
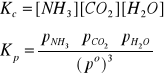
Stopień przereagowania substratów a stała równowagi![]()
Stopień przereagowania substratu (α) jest miarą zaawansowania reakcji chemicznej. Wielkość tę definiujemy wzorem:
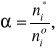
gdzie ni* jest licznością i-tego substratu, który przereagował w danej reakcji, a nio jest jego licznością początkową.
Liczność (ni) nieprzereagowanego i-substratu obliczamy z bilansu materiałowego:
![]()
W układzie zamkniętym o stałej objętości V, stopień przereagowania można obliczyć stosując wzór:
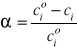
Stopień przereagowania zmienia się granicach 0 < α ≤ 1 lub 0 < α ≤ 100%.
Znając skład wyjściowej mieszaniny substratów
i stopień przereagowania jednego z nich, można na podstawie równania stechiometrycznego danej reakcji oraz znanej objętości układu reakcyjnego obliczyć stężenia substratów i produktów w stanie równowagi
i wyznaczyć wartość stężeniowej stałej równowagi.
Przykłady:
W temperaturze 520 K do naczynia o objętości 1 dm3 wprowadzono 1,00 mol PCl5. W stanie równowagi stopień przereagowania PCl5 jest równy 14,0%. Obliczyć stałą Kc reakcji PCl5 ↔ PCl3 + Cl2.
|
PCl5 |
PCl3 |
Cl2 |
Na początku |
1,00 |
- |
- |
Przereagowało |
-0,14 |
0,14 |
0,14 |
Stan równowagi |
0,86 |
0,14 |
0,14 |
Obliczamy stężenia równowagowe:
[PCl5] = 0,86, [PCl3] = 0,14, [Cl2] = 0,14
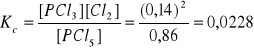
Do naczynia o objętości 0,5 dm3 wprowadzono 1,00 mol wodoru i 1,00 mol jodu. W temperaturze 476 K stała Kc reakcji H2 + I2 ↔ 2HI jest równa 45,2. Obliczyć stężenia reagentów w stanie równowagi.
|
H2 |
I2 |
HI |
Na początku |
1,00 |
1,00 |
- |
Przereagowało |
-x |
-x |
2x |
Stan równowagi |
1,00 - x |
1,00 - x |
2x |
[H2] = (1,00 - x)/0,5, [I2] = (1,00 - x)/0,5, [HI] = 2x/0,5
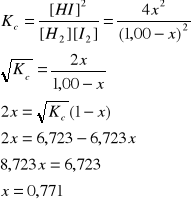
[H2] = [I2] = 0,458 mol/dm3, [HI] = 3,08 mol/dm3
XI.V. Wpływ temperatury, ciśnienia i stężeń reagentów
na stan równowagi. Reguła przekory
Na stan równowagi w układzie reakcyjnym wpływają zmiany temperatury, ciśnienia i stężeń reagentów. Zmiany te powodują przesunięcie stanu równowagi reakcji odwracalnej w kierunku substratów lub w kierunku produktów, ponieważ układ przeciwdziała tym zmianom zgodnie z regułą przekory.
Reguła przekory Przy zmianie jednego z parametrów zewnętrznych, temperatury lub ciśnienia, lub zmianie stężenia substratu lub produktu, układ przeciwdziała tym zmianom dążąc do nowego stanu równowagi. |
Rozpatrzymy to na przykładzie reakcji syntezy amoniaku:
N2 + 3H2 ↔ 2 NH3, ΔH < 0.
W zależności od czynnika zakłócającego stan równowagi, możliwe są następujące przeciwdziałania układu:
Zaburzenie stanu równowagi przez: |
Przeciwdziałanie układu w kierunku: |
dodanie substratów |
produktów |
usunięcie produktów |
produktów |
obniżenie ciśnienia |
większej liczby cząstek |
podwyższenie ciśnienia |
mniejszej liczby cząstek |
obniżenie temperatury |
przebiegu egzotermicznego |
podwyższenie temperatury |
przebiegu endotermicznego |
Szybkość reakcji chemicznej
CO2 + H2 → CO + H2O
stan równowagi
CO + H2O → CO2 + H2
Wyszukiwarka
Podobne podstrony:
Wyklad VI, chemia ogólna
Wykład IV, chemia ogólna
Wyklad VIII, chemia ogólna
Wyklad IX, chemia ogólna
Cząsteczka (VB), CHEMIA, semestr 1, chemia ogólna, wykłady
Chemia ogolna wyklady 5 6 2012 Nieznany
Wykład 3. Reakcje chemiczne, chemia, CHEMIA OGÓLNA -Walkowiak- (WPC 1002w) DOC
Chemia ogólna wykład 2 2012
Zakres materiału obowiązujący na II kolokwium wykładowe, Chemia ogólna i nieorganiczna, giełdy
Wyklad 6. Uklad okresowy pierwiastkow, pwr biotechnologia(I stopień), I semestr, Chemia ogólna
Wyklad 11a. Elektrolity, pwr biotechnologia(I stopień), I semestr, Chemia ogólna
Wyklad 11b. Elektrolity - cd., pwr biotechnologia(I stopień), I semestr, Chemia ogólna
Wyklad 12. Reakcje jadrowe, pwr biotechnologia(I stopień), I semestr, Chemia ogólna
Wykład 5. Elektronowa struktura atomu, chemia, CHEMIA OGÓLNA -Walkowiak- (WPC 1002w) DOC
Chemia ogólna wykład 4 2012
Chemia ogólna wykład 7 2012
Slownik ChemLab, Studia, Chemia ogólna wykład
więcej podobnych podstron