EKONOMETRIA - WYKŁADY.
Wykład z dnia 28.04.2012 r.
W przypadku rozważanych przez nas modeli z jedną zmienną objaśniającą, współczynnik determinacji r2 równy jest kwadratowi współczynnika korelacji między zmienną objaśnianą a objaśniającą.
Ten ostatni ma wzór:
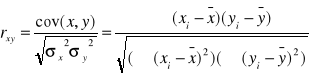
gdzie:
![]()
- współczynnik korelacji Pearsona pomiędzy zmienną objaśnianą Y a zmienną objaśniającą X
![]()
- kowariancja zmiennych X i Y
![]()
- wariancja odpowiednich zmiennych X i Y
![]()
gdzie:
![]()
- odchylenia standardowe odpowiednio zmiennych X i zmiennych Y
Podnosząc ostatni wzór do kwadratu mamy że 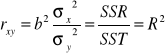
Nie można jednoznacznie określić co to jest wysoki współczynnik determinacji.
Dla modeli których parametry estymowane są na podstawie szeregów czasowych często R2 są rzędu 0,9 ≤ R2 ≤95 .
W przypadku danych przekrojowych czasowych i przekrojowych estymowane w praktyce R2 są znacznie niższe współczynniki determinacji.
R2 może być obliczony zawsze bez względu na postać modelu i zastosowaną metodę estymacji jednakże interpretacje w kategoriach wariancji objaśnianej i nieobjaśnianej oraz własności są zachowane tylko przy spełnieniu trzech warunków:
Prawdziwa relacja między zmienną X a zmienną Y populacji generalnej musi być liniowa wówczas bowiem R2 daje informację ile procent zmienności zmiennej Y zostało objaśnione przez liniową funkcję zmiennej objaśniającej.
Parametry muszą być estymowane metodą najmniejszych kwadratów. Wykorzystanie innej metody powoduje iż R2 może przybrać dowolną wartość rzeczywistą co znacznie komplikuje interpretacje wyniku.
Model musi zawierać wyraz wolny w przeciwnym przypadku 1 ≤ R2 <

Przykłady funkcji nieliniowej sprowadzonych do postaci liniowej względem parametrów.
Funkcja potęgowa.
![]()
![]()
Postać liniowa względem parametrów daje:
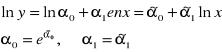
Funkcja wykładnicza.
![]()
Postać liniowa względem parametrów daje:
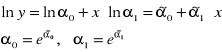
Funkcja wykładnicza z odwrotnością.
![]()
Postać liniowa względem parametrów daje:
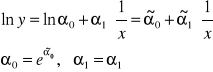
Funkcja potęgowo - wykładnicza.
![]()
Postać liniowa względem parametrów daje:
![]()
![]()
Funkcja potęgowo - wykładnicza z odwrotnością.
![]()
Postać liniowa względem parametrów daje:
![]()
![]()
Parabola logarytmiczna.
![]()
Postać liniowa względem parametrów daje:
![]()
![]()
Hiperbola.
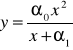
Postać liniowa względem parametrów daje:
![]()
![]()
Warto wyznaczyć również standardowy błąd szacunku modelu a także średnie błędy parametry szacunku b0, b1.
Standardowy błąd szacunku modelu wyznaczany według modelu:
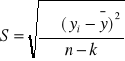
gdzie:
n - liczba obserwacji
k - liczba szacowanych parametrów , w naszym przypadku k = 2
Średnie błędy szacunku parametru wyznaczamy według wzoru:
![]()
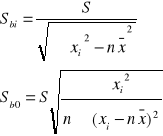
Po oszacowaniu parametrów modelu należy sprawdzić czy opisana przez równanie zależność jest istotna.
Można się w tym celu posłużyć testem istotności t studenta korzystając ze wzoru:
![]()
Dla zbadania istotności zależności należy sprawdzić hipotezę zerową .
H0 ; b1 = 0
Wskazuje to że jest brak zależności między badanymi zmiennymi Y oraz X wobec hipotezy alternatywnej
H1 ; b1 ≠ 0
Jeżeli zachodzi zależność ![]()
Gdzie:
![]()
- spełnia warunek ![]()
![]()
- poziom istotności przyjmowanej zazwyczaj ![]()
![]()
- wartość graniczna odczytywana z odpowiednich tablic jeżeli ![]()
to odrzucamy hipotezę zerową na rzecz hipotezy alternatywnej.
Interpretacja ekonomiczna parametrów modelu liniowego zależy od jednostki w których są wyrażone badane zmienne.
W naszym przypadku parametry strukturalne b1 - mówi o tym o ile zwiększy się wartość zmiennej objaśnianej Y jeżeli X wzrośnie o jednostkę .
Obliczony błąd szacunku informuje że wzrost zmiennej Y mieści się w granicach b1 - Sb1 ≤ Y ≤ b1 + Sb1
Korelacja i regresja wielu zmiennych.
Uwzględniając wzajemny związek wielu zmiennych Y, X1 , X2 , … , Xk
Gdzie:
Y - zmienna zależna
X1 , X2 , Xk - zmiennymi niezależnymi
Problem korelacji i regresji można badać dwojako:
Wielorako - jeśli uwzględnimy oddziaływanie na zmienną zależną Y wszystkich zmiennych niezależnych X1 , X2 , Xk
W pierwszym przypadku oblicza się współczynnik korelacji wielorakiej i szacuje się model korelacji wielorakiej.
Cząstkowo, jeśli badamy współzależność tylko dla niektórych zmiennych eliminując wpływ pozostałych.
W drugim przypadku oblicza się współczynniki regresji cząstkowej , współczynniki korelacji cząstkowej.
Korelacja cząstkowa i wieloraka.
Jeżeli na pewną zmienną objaśnianą Y oddziałuje więcej niż jedna zmienna objaśniająca X , a interesuje nas ścisłość związków korelacyjnych jedynie między dwiema zmiennymi przy wyłączeniu wpływu innych zmiennych to wykorzystujemy miary ścisłości związku zwanym współczynnikiem korelacji cząstkowej oznaczamy je:
![]()
Pierwsze subskrypty oznaczają cechy między którymi poszukujemy korelacji , natomiast subskrypty po kropce oznaczają cechy które chcemy wyeliminować.
Do obliczenia współczynnika korelacji cząstkowej wygodnie jest posłużyć się rachunkiem macierzystym.
Współczynnik korelacji cząstkowej dowolnego rzędu obliczamy z ogólnego wzoru:
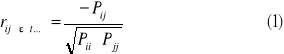
Gdzie:
Pij - jest dopełnieniem algebraicznym macierzy P współczynnikiem korelacji po wszystkich łączonych do analizy zmiennych powstałym przez skreślenie i -tego wiersza i j - kolumny,
Pii oraz Pjj - są odpowiednimi dopełnieniami algebraicznymi macierzy P powstałymi przez określenie jej i - tego wiersza i i - tej kolumny oraz jej j- tego wiersza i j - tej kolumny.
Jak wynika ze wzoru 1 do obliczania współczynnika korelacji cząstkowej niezbędna jest znajomość współczynnika korelacji całkowitej wszystkich rozpatrywanych zmiennych.
Współczynniki korelacji całkowitej są elementem:
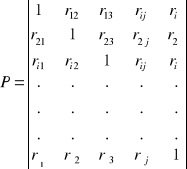
Macierz P jest macierzą symetryczną tzn, że rij = rji .
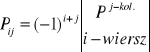
Jeśli weźmiemy pod uwagę trzy zmienne to podstawą do obliczania współczynnika korelacji cząstkowej jest wówczas macierz P o wymiarach 3 x 3 .
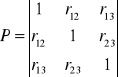
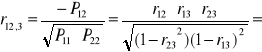
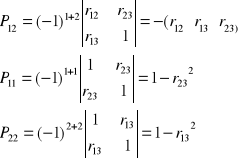
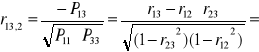
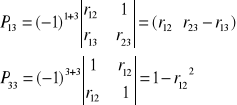
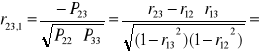
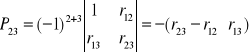
Wyszukiwarka
Podobne podstrony:
PRAWO FINANSOWE 29.04.2012, II rok, Wykłady, Prawo finansowe
PRAWO FINANSOWE 27.04.2012, II rok, Wykłady, Prawo finansowe
PRAWO FINANSOWE 13.04.2012, II rok, Wykłady, Prawo finansowe
PRAWO FINANSOWE 29.04.2012, II rok, Wykłady, Prawo finansowe
EKONOMETRIA 29.04.2012, II rok, Ćwiczenia, Ekonometria
EKONOMETRIA 09.03.2012, II rok, Wykłady, Ekonometria
EKONOMETRIA 15.04.2012, II rok, Ćwiczenia, Ekonometria
EKONOMETRIA 11.05.2012, II rok, Wykłady, Ekonometria
POLITYKA SPOŁECZNA 12.02.2012, II rok, Wykłady, Polityka społeczna
PRAWO FINANSOWE 25.03.2012, II rok, Wykłady, Prawo finansowe
POLITYKA SPOŁECZNA 11.05.2012, II rok, Wykłady, Polityka społeczna
PODSTAWY MAKROEKONOMII 03.06.2012, II rok, Wykłady, Podstawy makroekonomii
PRAWO FINANSOWE 11.03.2012, II rok, Wykłady, Prawo finansowe
PRAWO FINANSOWE 26.02.2012, II rok, Wykłady, Prawo finansowe
PRAWO FINANSOWE 12.05.2012, II rok, Wykłady, Prawo finansowe
PODSTAWY MAKROEKONOMII 23.03.2012, II rok, Wykłady, Podstawy makroekonomii
PODSTAWY MAKROEKONOMII 11.02.2012, II rok, Wykłady, Podstawy makroekonomii
EKONOMETRIA 25.03.2012, II rok, Ćwiczenia, Ekonometria
EKONOMETRIA 26.02.2012, II rok, Ćwiczenia, Ekonometria
więcej podobnych podstron