Laboratorium Hydromechaniki |
||
Grupa/gr. lab.
II/4 |
Temat ćwiczenia: Pomiar natężenia przepływu z wykorzystaniem rurki P-P, zwężki Venturiego, kryzy ISA.
|
Lab wykonano 01.03.2004 |
|
|
Data oddania: 15.03.2004 |
WNiG rok II
|
Imię i nazwisko: Tomasz Łakomy, Bartłomiej Kumala, Jakub Zieliński
|
Ocena: |
Celem ćwiczenia jest wyznaczenie zależności liczby przepływu α od liczby Reynoldsa Re dla zwężek. Wykres α = α (Re) umożliwia wyznaczenie strumienia objętości (objętościowego natężenia przepływu) płynu na podstawie pomiaru różnicy ciśnień na kryzie lub dyszy.
1. Część teoretyczna:
Zwężka zabudowana w rurociągu powoduje zmniejszenie przekroju poprzecznego, a tym samym wzrost średniej prędkości przepływu i energii kinetycznej oraz spadek ciśnienia statycznego. W tym ćwiczeniu wykorzystano kryzę ISA, dyszę Venturiego i rurkę P-P. otwory impulsowe do odbioru ciśnienia statycznego przed i za kryzą zostały wykonane w pewnych podanych przez normę odległościach od jej tarczy. Dysza Venturiego jest dyszą z długim dyfuzorem czyli taką, w której większa średnica dyfuzora jest równa średnicy przewodu. Otwory impulsowe znajdują się na stronie dopływowej w obudowie dyszy, zaś po stronie odpływowej - w jej cylindrycznym przewężeniu.
Rurka P- P jest ....
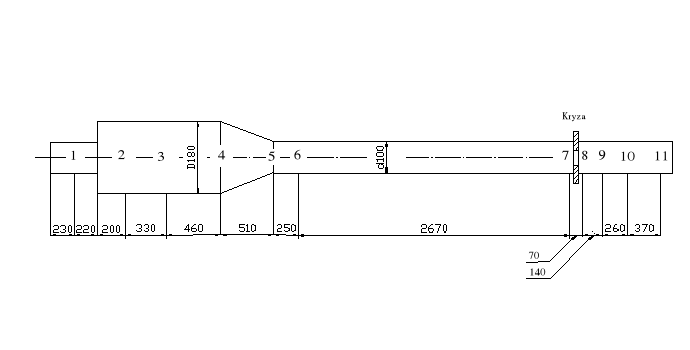
2. Przebieg ćwiczenia:
Strumień objętości mierzy się rotametrem lub gazomierzem. Różnicę ciśnień należy zmierzyć manometrem dzwonowym. Połączenie zwężek z ciśnieniomierzem następuje przez odpowiednie ustawienie przełącznika. Należy obliczyć gęstość powietrza - zmierzyć temperaturę termometru suchego i mokrego. Zmierzyć prędkość przepływu dla zwężki, kryzy i rurki P-P.
W ćwiczeniu wykorzystaliśmy następujące dane:
Promień przewodu R = 75mm
Promień łuku kolana R1 = 570 mm
Średnica kryzy Dk = 106 mm
Średnica zwężki Dz = 95 mm
Liczba przepływu dla kryzy αk = 0,723
Liczba przepływu dla zwężki αz = 1,12
Liczba przepływu dla rurki P-P = 0,80
ρcm = 800 kg/m3
ρpowietrza = 1,16 kg/m3
Wzory wykorzystane do obliczeń:
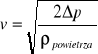
![]()
- do wykresu
![]()
![]()
3. Uzyskane obliczenia:
Pomiar |
Dl |
d |
V |
Przełożenie |
Dh |
Dp |
V |
|
Q |
Re |
1P-P |
1 |
570 |
2 |
0,5 |
0,5 |
3920000 |
98,99494937 |
0,8 |
1,399508 |
619 565 217 |
2P-P |
10 |
570 |
6 |
0,5 |
5 |
39200000 |
313,0495168 |
0,8 |
4,425633 |
1 858 695 652 |
3P-P |
5 |
570 |
4,5 |
0,5 |
2,5 |
19600000 |
221,3594362 |
0,8 |
3,129395 |
1 394 021 739 |
4P-P |
1 |
570 |
1,8 |
0,5 |
0,5 |
3920000 |
98,99494937 |
0,8 |
1,399508 |
557 608 696 |
5P-P |
4 |
570 |
3,5 |
0,5 |
2 |
15680000 |
197,9898987 |
0,8 |
2,799016 |
1 084 239 130 |
6P-P |
8 |
570 |
5,5 |
0,5 |
4 |
31360000 |
280 |
0,8 |
3,958407 |
1 703 804 348 |
7P-P |
1,5 |
570 |
0,5 |
0,5 |
0,75 |
5880000 |
121,2435565 |
0,8 |
1,71404 |
154 891 304 |
1Z |
14,5 |
95 |
2 |
0,2 |
2,9 |
22736000 |
238,4114091 |
1,12 |
4,718647 |
103 260 870 |
2Z |
53,5 |
95 |
6 |
0,2 |
10,7 |
83888000 |
457,9519625 |
1,12 |
9,063801 |
309 782 609 |
3Z |
34,5 |
95 |
4,5 |
0,2 |
6,9 |
54096000 |
367,749915 |
1,12 |
7,278519 |
232 336 957 |
4Z |
13,5 |
95 |
1,8 |
0,2 |
2,7 |
21168000 |
230,0434742 |
1,12 |
4,553028 |
92 934 783 |
5Z |
23,5 |
95 |
3,5 |
0,2 |
4,7 |
36848000 |
303,5127674 |
1,12 |
6,007135 |
180 706 522 |
6Z |
46,5 |
95 |
5,5 |
0,2 |
9,3 |
72912000 |
426,9426191 |
1,12 |
8,450063 |
283 967 391 |
7Z |
11,5 |
95 |
0,5 |
0,2 |
2,3 |
18032000 |
212,3205124 |
1,12 |
4,202255 |
25 815 217 |
1K |
9 |
106 |
2 |
0,5 |
4,5 |
35280000 |
296,9848481 |
0,723 |
3,794416 |
115 217 391 |
2K |
32 |
106 |
6 |
0,5 |
16 |
125440000 |
560 |
0,723 |
7,15482 |
345 652 174 |
3K |
20 |
106 |
4,5 |
0,5 |
10 |
78400000 |
442,7188724 |
0,723 |
5,656382 |
259 239 130 |
4K |
8 |
106 |
1,8 |
0,5 |
4 |
31360000 |
280 |
0,723 |
3,57741 |
103 695 652 |
5K |
13 |
106 |
3,5 |
0,5 |
6,5 |
50960000 |
356,931366 |
0,723 |
4,560321 |
201 630 435 |
6K |
27 |
106 |
5,5 |
0,5 |
13,5 |
105840000 |
514,392846 |
0,723 |
6,572122 |
316 847 826 |
7K |
7 |
106 |
0,5 |
0,5 |
3,5 |
27440000 |
261,9160171 |
0,723 |
3,346361 |
28 804 348 |
4. Wykres otrzymany na podstawie wyników w tabeli:
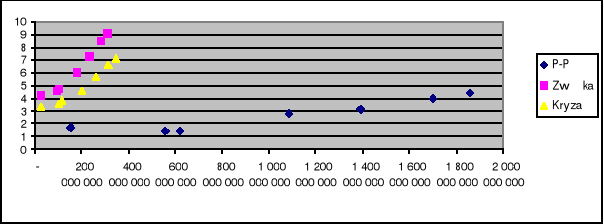
Wyszukiwarka
Podobne podstrony:
Laboratorium Hydromechaniki - †w.4, mechanika plynów
Hydromechanika ćwicz.1, mechanika plynów
LAB MECHANIKA PLYNOW 2, ATH, Mechanika płynów, moje
Laboratorium Hydromechaniki - ćw.4, mechanika plynów
Mechanika Plynow Lab, Sitka Pro Nieznany
Lab. mech. płynów-Wizualizacja opływu walca w kanaliku, Mechanika Płynów pollub(Sprawozdania)
Mechanika Płynów Lab, Sitka N19
Mechanika Płynów Lab, Sitka N4
Mechanika Płynów Lab, Sitka N12
Mechanika Płynów Lab, Sitka N14
sprawozdanie z mechaniki płynów Lab 3
sprawko 2, PWR, Inżynieria Środowiska, semestr 3, mechanika płynów, mechanika płynów lab
Mechanika Płynów Lab, Sitka N13
Mechanika Płynów Lab, Sitka N9
mechanika płynów lab 1 sprawko
sprawozdanie z mechaniki płynów Lab 3krzys
więcej podobnych podstron