6A Całka ogólna równania różniczkowego

(1)

Lewą stronę równania traktujemy jak zwykłe równanie kwadratowe i obliczamy deltę

y” - 5y'+ 6y = 0
r” - 5r' + 6r = 0 w miejsca y wstawiamy r

Delta =1

Miejsca zerowe:

r₁₌2 lub r₂=3

Jeżeli r₁ i r₂ są liczbami rzeczywistymi to funkcja ma postać (jeśli mam 2 różne miejsca zerowe):

(2)

Gdy ma 1 miejsce zerowe r₁ = r₂ = r₀ wówczas ma funkcja taką postać:

Rozwiązaniem tego równania są liczby 2 i 3 ( w miejsce r₁ i r₂ wstawiamy rozwiązania do równania 2) wobec tego całka ogólna równania jednorodnego CORJ ma postać:

Po prawej stronie równania (1) jest równanie kwadratowe -2+x²

y=Ax²+Bx + C jest to ogólne równanie kwadratowe

(1)

Skoro y” = 0 i y'=A to

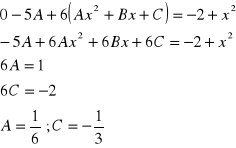
Rowziąznie równaia

6B Całka ogólna równania różniczkowego

(1)

Lewą stronę równania traktujemy jak zwykłe równanie kwadratowe i obliczamy deltę

y” - 4y'+ 13y = 0
r” - 4r' +13r = 0 w miejsca y wstawiamy r

Delta <0

Miejsca zerowe:

r₁₌2+3i lub r₂=2-3i a = 2 b=3

Prawa stronę równania :

Rozwiązujemy przez przewidywanie, że całka ogólna ma postać:

oraz pochodna 1

z tego robimy jeszcze raz pochodną 2

Wstawiamy do (1) w miejsca y , y', y'' i mamy

teraz przyrównujemy współczynniki przy sinx i cos x;

8m+9n = 1

-8n+9m = 0 otrzymujemy
w stawiamy do y₂

Wiemy też ,że

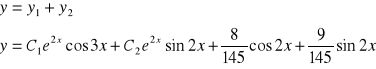
CORR

6C

6D

y''-7y'+ 6y= 2x-1 (1)

zamieniamy lewą stronę na

r”-7r'+6r= 0 i przyrównujemy do zera

obliczamy delte
i
oraz miejsca zerowe
>0

r₁= 1

r₂ = 6

Jeżeli r₁ i r₂ są liczbami rzeczywistymi to funkcja ma postać (jeśli mam 2 różne miejsca zerowe):

wiemy ,że y”=0 i y'=A i y=Ax+B ( y' i y''czyli pochodne z y pierwsza i druga) wyznaczamy A i B wstawiając do (1)

0-7A+6(Ax+B)=2x-1

6Ax-7A+6B=2x-1

6A=2 => A=

-7A+6B = -1 B=

Ostatecznie

CORR

6E

y''+4y'+ 3y= x-1 (1)

zamieniamy lewą stronę na

r”+4r'+3r= 0 i przyrównujemy do zera

obliczamy delte
i
oraz miejsca zerowe
>0

r₁= -3

r₂ = -1

Jeżeli r₁ i r₂ są liczbami rzeczywistymi to funkcja ma postać (jeśli mam 2 różne miejsca zerowe):

wiemy ,że y”=0 i y'=A i y=Ax+B ( y' i y''czyli pochodne z y pierwsza i druga) wyznaczamy A i B wstawiając do (1)

0+4A+3(Ax+B)=x-1

3Ax+4A+3B=x-1

3A=1 => A=

4A+3B = -1 B=

Ostatecznie

CORR

6F

y''+4y'+ 3y= 9x+9 (1)

zamieniamy lewą stronę na

r”+4r'+3r= 0 i przyrównujemy do zera

obliczamy delte
i
oraz miejsca zerowe
>0

r₁= -3

r₂ = -1

Jeżeli r₁ i r₂ są liczbami rzeczywistymi to funkcja ma postać (jeśli mam 2 różne miejsca zerowe):

wiemy ,że y”=0 i y'=A i y=Ax+B ( y' i y''czyli pochodne z y pierwsza i druga) wyznaczamy A i B wstawiając do (1)

0+4A+3(Ax+B)=9x+9

3Ax+4A+3B=9x+9

3A=9 => A=

4A+3B = 9 B=

Ostatecznie

CORR

6G

y''+5y'+ 4y= 12x+7 (1)

zamieniamy lewą stronę na

r”+5r'+4r= 0 i przyrównujemy do zera

obliczamy delte
i
oraz miejsca zerowe
>0

r₁= -4

r₂ = -1

Jeżeli r₁ i r₂ są liczbami rzeczywistymi to funkcja ma postać (jeśli mam 2 różne miejsca zerowe):

wiemy ,że y”=0 i y'=A i y=Ax+B ( y' i y''czyli pochodne z y pierwsza i druga) wyznaczamy A i B wstawiając do (1)

0+5A+4(Ax+B)=9x+9

4Ax+5A+4B=9x+9

4A=12 => A=

5A+4B = 7 B=

Ostatecznie

CORR

---