Rynek kapitałowy doskonale konkurencyjny

1. Dwuokresowy model podejmowania decyzji

2. Krzywa podaży oszczędności

3. Zdyskontowana wartość bieżąca

4. Wyznaczanie stopy procentowej w

równowadze

5. Kapitał ludzki i popyt na wykształcenie

6. Eksploatacja nieodnawialnych zasobów

naturalnych

7. Odnawialne zasoby naturalne - drzewa

8. Optymalne zarządzanie rybołówstwem

*

Dwuokresowy model podejmowania decyzji

Wykorzystujemy model z dwoma dobrami równowagi konsumenta, który ma preferencje dotyczące rozłożenia konsumpcji w czasie: C₁ - bieżącej i C₂ - przyszłej, zapisane w postaci funkcji użyteczności: U(C₁, C₂) (rys. 18.1). MRS to krańcowa stopa preferencji czasowych:

mierzona wzdłuż krzywych obojętności.

Międzyokresowe ograniczenie budżetowe

W każdym okresie konsument dostaje dochód: M₁ w okresie bieżącym i M₂ w okresie przyszłym. Konsumpcję w każdym okresie można zmieniać. Dzięki zaciąganiu pożyczek zgodnie z rynkową stopą procentową konsument może zwiększyć konsumpcję bieżącą, a dzięki oszczędzaniu przy tej stopie może zwiększyć konsumpcję okresu przyszłego. Każda pożyczka zaciągnięta w okresie bieżącym musi być zwrócona z dochodu okresu przyszłego oraz wszystkie oszczędności bieżące zwiększają przyszły dochód.

Oszczędności: część dochodu okresu bieżącego pozostała po opłaceniu bieżącej konsumpcji: S = M₁ - p₁C₁, gdzie p₁ to indeks cenowy konsumpcji bieżącej. Oszczędności mogą być ujemne jeśli konsument zaciąga pożyczki na sfinansowanie konsumpcji bieżącej.

Kwota dostępna na konsumpcję w okresie przyszłym to dochód w tym okresie powiększony o oszczędności i odsetki od nich. Jeżeli oszczędności są ujemne, to w okresie przyszłym konsument musi spłacić zaciągniętą pożyczkę i zapłacić odsetki od niej w okresie przyszłym. Oczywiście zmniejsza to wielkość konsumpcji w okresie przyszłym.

Konsumpcja w okresie przyszłym:

p₂C₂ = M₂ + S + iS = M₂ + (1 + i)S, gdzie i to rynkowa stopa procentowa. Po wstawieniu wzoru na oszczędności do równania konsumpcji w okresie następnym otrzymujemy:

p₂C₂ = M₂ + (1 + i)(M₁ - p₁C₁) = M₂ + (1 + i)M₁ - p₁(1 + i)C₁.

Po przekształceniu:

p₂C₂ + p₁(1 + i)C₁ = M₂ + (1 + i)M₁ .

Jest to równanie ograniczenia budżetowego w modelu dwuokresowym, w którym wydatki znajdujące się po lewej stronie równają się całkowitemu dochodowi w obu okresach po prawej stronie równania.

Stopa inflacji: d jest to procentowa zmiana cen następująca między okresem bieżącym i przyszłym: d = (p₂ - p₁)/p₁. Przekształcając: p₂ = (1 + d)p₁.

Po wstawieniu wzoru na poziom cen w okresie przyszłym,

p₂ = (1 + d)p₁, do równania ograniczenia budżetowego:

p₁(1 + d)C₂ + p₁(1 + i)C₁ = M₂ + (1 + i)M₁ .

Z tego równania wynika, że linia dwuokresowego ograniczenia budżetowego ma dwa punkty przecięcia z osiami:

jeżeli C₁ = 0

jeżeli C₂ = 0.

Przy konstruowaniu równania ograniczenia budżetowego przyjęliśmy, że konsument nie musi oszczędzać ani zaciągać pożyczek wydając w każdym okresie dochód, czyli: p₁C₁ = M₁ i p₂C₂ = M₂(1 + d)p₁C₂, co po przekształceniu daje:

C₁ = M₁/p₁ i C₂ = M₂/(1 + d)p₁.

Każde odejście od tego punktu oznacza, że konsument jest pożyczkobiorcą netto lub oszczędzającym netto. Jeżeli C₁ > M₁/p₁ , to konsument wydaje na konsumpcję w okresie bieżącym więcej niż zarabia, czyli jest pożyczkobiorcą netto. Jeżeli C₂ > M₂/[(1 +d)p₁], to konsument wydaje na konsumpcję w okresie przyszłym więcej niż zarabia, jest więc oszczędzającym netto.

Rys. 18.2: linia międzyokresowego ograniczenia budżetowego. Z punktów przecięcia można obliczyć jej nachylenie: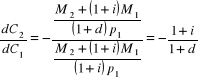
.

Można je interpretować na kilka sposobów:

1)jest to rzeczywisty koszt dodatkowej jednostki konsumpcji dzisiaj w przeliczeniu na konsumpcję jutro - międzyokresowy stosunek cen: Jeżeli kupujemy coś dzisiaj, to tracimy odsetki, które zarobilibyśmy, ale te odsetki muszą być zdyskontowane stopą zgodnie z którą ceny zmieniają się między okresem bieżącym i przyszłym.

2) jest to realna stopa określająca zwiększanie się siły nabywczej oszczędności: jeżeli stopa inflacji = stopie procentowej, to stopa ta = 1, z czego wynika, że siła nabywcza oszczędności nie zmienia się pomimo dodatniej stopy procentowej; jeżeli i > d, to stopa > 1, czyli siła nabywcza rośnie; przy stopie < 1 siła nabywcza oszczędności maleje.

Międzyokresowa maksymalizacja użyteczności

Po połączeniu rys. 18.1 i 18.2 widzimy, że konsument wybiera kombinację konsumpcji przyszłej i bieżącej aby maksymalizować użyteczność przy międzyokresowym ograniczeniu budżetowym. A więc musi być spełniony warunek równych nachyleń: MRS (wewnętrzny stosunek cen) równa się zewnętrznemu stosunkowi cen, czyli MRTP równa się międzyokresowemu stosunkowi cen:
.

Rys. 18.3: lewa część - pożyczkobiorca netto maxU na prawo od punktu S = 0; prawa - oszczędzający netto maxU na lewo od tego punktu.

Wzrost stopy procentowej

Zał.: i₂ > i₁. Punkt, w którym S = 0 nie reaguje na zmiany i. Dlatego nowa linia ograniczenia budżetowego musi przechodzić przez ten punkt, czyli:

C₁ = M₁/p₁ i C₂ = M₂/(1 + d)p₁.

Linia ograniczenia budżetowego obraca się w tym punkcie, a więc punkt przecięcia z osią pionową zwiększa się:

,

punkt przecięcia z osią poziomą maleje:

.

Rys. 18.4: obrót linii ograniczenia budżetowego w punkcie

S = 0.

Statyka porównawcza wzrostu stopy procentowej

Ponieważ linia ograniczenia budżetowego obraca się w punkcie S = 0 przy i↑ to inaczej oddziałuje na pożyczkodawcę netto i pożyczkobiorcę netto. Efekt substytucyjny działa tak samo na obydwu, gdyż linia przyjmuje ostrzejsze nachylenie. Oznacza to, że realna cena konsumpcji bieżącej rośnie:
. Działanie efektu substytucyjnego zarówno dla pożyczkobiorcy, jak i dla pożyczkodawcy polega na ograniczaniu konsumpcji bieżącej.

Oddziaływanie efektu dochodowego wzrostu stopy procentowej na konsumpcję bieżącą zależy od tego czy konsument jest pożyczkodawcą, czy też pożyczkobiorcą. Pożyczkodawca potencjalnie może zarobić większy dochód - zwiększają się odsetki od oszczędności. Pożyczkobiorca będzie miał mniejszy dochód ze względu na wzrost odsetek, jakie musi zapłacić za pożyczkę służącą zwiększeniu konsumpcji bieżącej. Jeżeli konsumpcja bieżąca jest dobrem normalnym, to pożyczkobiorca netto zawsze zmniejszy konsumpcje.

b

Dzieje się tak, gdyż ED (jak ES) działa w kierunku ograniczania konsumpcji przy obrocie linii ograniczenia budżetowego „do początku układu współrzędnych” - rys. 18.5. Dla pożyczkodawców ED działa w kierunku zwiększania konsumpcji bieżącej przy obrocie linii ograniczenia budżetowego „od początku układu współrzędnych”. Pożyczkodawca może konsumować mniej w okresie bieżącym, gdy ES jest silniejszy od ED lub więcej przy dominacji ED nad ES - rys. 18.6.

Krzywa podaży oszczędności

Z rys. 18.5 i 18.6 można wyprowadzić krzywą popytu na konsumpcję w okresie bieżącym. Konsumpcja bieżąca jest funkcją: stopy procentowej, przy stałych wartościach: dochodu bieżącego i przyszłego, indeksu cen konsumpcji bieżącej i stopy inflacji, czyli:
. Po wstawieniu wzoru na funkcję konsumpcji do definicji oszczędności,

S = M₁ -p₁C₁, możemy skonstruować funkcję oszczędności jako funkcję od stopy procentowej przy pozostałych wielkościach stałych:
.

Rys. 18.7: wyprowadzenie funkcji dla pożyczkobiorcy dla konsumpcji jako dobra normalnego. Ponieważ ES i ED działają w tym samym kierunku, to krzywa popytu na konsumpcję bieżącą ma nachylenie ujemne. Po odjęciu ceny pomnożonej przez krzywą popytu na konsumpcję bieżącą od M₁ otrzymujemy funkcję podaży oszczędności o wartościach ujemnych i dodatnim nachyleniu. Pożyczkobiorca pożycza mniej przy i↑. Analogiczną dodatnią funkcją byłaby opadająca funkcja popytu na kredyty: L_d = p₁C₁ - M₁.

Rys. 18.8: funkcja popytu na konsumpcję bieżącą i funkcja podaży oszczędności pożyczkodawcy przy konsumpcji bieżącej będącej dobrem normalnym. Przy pewnej nieujemnej stopie procentowej konsument staje się pożyczkodawcą z pożyczkobiorcy. Na początku S↑ przy i↑. ES dominuje nad ED. Przy odpowiednio wysokiej i ED zaczyna dominować nad ES i S↓ przy i↑, czyli konsument kupuje więcej w okresie bieżącym pomimo i↑.

Po połączeniu analizy pożyczkobiorcy i pożyczkodawcy: rys. 18.9:

Zdyskontowana wartość bieżąca

Po wyprowadzeniu funkcji oszczędności przechodzimy do inwestycji w nowy kapitał. Ponieważ urządzenia, budynki i inne formy kapitału fizycznego zatrudniane są przez firmy w ciągu wielu okresów, to wymuszają podejmowanie decyzji międzyokresowych. Nowy kapitał świadczy więc strumień usług w czasie. Ponieważ wielkości płatności są różnie rozłożone w czasie przy zakupie i przy leasingu, to firma potrzebuje pewnych standardowych wzorców do porównań dotyczących nabywania dóbr kapitałowych.

Wyprowadzenie wzoru na zdyskontowaną wartość bieżącą (DPV)

Aby wyprowadzić właściwą podstawę do porównań bieżącej płatności i strumienia płatności zaczynamy od wyprowadzenia bieżącego kosztu strumienia płatności.

Odsetki składane (kapitalizacja złożona):

i - rynkowa stopa procentowa (stała dla T lat)

D_T - depozyt początkowy (na T lat )

V_T - skapitalizowana wartość D_T po T latach

Obliczamy wartość D_T:

V₁ = D_T (1 + i)

V₂ = V₁(1 + i) = D_T (1 + i) (1 + i) = D_T (1 + i)²

V_T = D_T (1 + i)^T

Rozwiązujemy dla: D_T:
. Wyrażenie 1/(1 + i)^T określane jest mianem czynnika dyskontującego, a D_T to (zdyskontowana) wartość bieżąca V_T.

Przyjmijmy, że przychód, r_t, jest podejmowany w każdym roku t z depozytu bankowego. Aby podjąć r₁ w roku 1 trzeba złożyć w banku depozyt równy wartości bieżącej skapitalizowanej wartości r₁ zwany D₁:
. Aby podjąć r₂ w roku 2 trzeba złożyć w banku depozyt równy wartości bieżącej skapitalizowanej wartości r₂ zwany D₂:
. Całkowita kwota, jaką należy wpłacić do banku aby co roku podejmować r_t przez T lat jest sumą wszystkich odpowiednich depozytów początkowych (lub wartości bieżacej) nazywaną zdyskontowaną wartością bieżącą strumienia przychodów: DPV_T = D₁ + D₂ + ... +D_T, czyli:
. Dla stałego r:
.

Wartość bieżąca strumienia rent wieczystych (równych płatności przy nieskończonym horyzoncie czasowym): co stanie się z
przy czasie dążącym do nieskończoności:

.

Przekształcamy: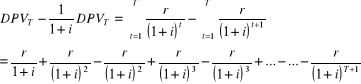
.

Po uporządkowaniu:
.

Rozwiązanie dla DPV_T:
.

Jeżeli T dąży do nieskończoności:
.

Po podstawieniu:

w granicy przy T dążącym do nieskończoności wartość bieżąca strumienia przychodów r rocznie równa się r podzielonemu przez stopę procentową, i.

Analogicznie:

r = i • DPV_T.

Wyznaczanie stopy procentowej w równowadze

Inwestycje jako funkcja stopy procentowej

Ponieważ DPV przy czasie nieograniczonym jest równa r/i, to firmie doskonale konkurencyjnej (w nieograniczonym czasie) będzie obojętne czy kupić kapitał, czy go wynająć przy stawce r za jednostkę rocznie. Cena doskonale konkurencyjna za jednostkę kapitału powinna równać się DPV na jednostkę:

DPV = r/i = p_K.

Jeżeli p_K > DPV, to firma wynajmowałaby cały swój kapitał. Jeżeli p_K < DPV, to firma kupowałaby cały swój kapitał. Przy p_K = DPV, firmie jest obojętne, czy kupuje, czy też wynajmuje.

Jeżeli nowy kapitał jest produkowany i sprzedawany na rynku doskonale konkurencyjnym, to możemy zapisać funkcję rynkowej podaży kapitału w postaci:

K_S = K_S(p_K),

gdzie: K_S to całkowita wielkość kapitału, jaką wszystkie firmy chcą sprzedać na rynku przy każdej DPV. Co więcej, w modelu równowagi ogólnej z tworzeniem nowego kapitału związane jest produkowanie mniejszej ilości dóbr konsumpcyjnych dzisiaj. Jeżeli wykresem funkcji możliwości produkcyjnych jest krzywa, to krzywa podaży kapitału w LR ma nachylenie dodatnie.

Całkowite wydatki na nowy kapitał są równe cenie pomnożonej przez funkcję podaży:

E_K = p_KK(p_K).

Aby określić zależność między wartością nowego kapitału i stopą procentową, spostrzegamy, że jeżeli K_S ma nachylenie dodatnie, to również E_K musi mieć nachylenie dodatnie. Jeżeli cena równowagi kapitału rośnie, to rośnie podaż kapitału i p_KK_S musi rosnąć.

Rys. 18.10: przekłada dodatnio nachyloną krzywą podaży kapitału na funkcję pokazującą zależność między stopą procentową i wydatkami na nowy kapitał. Górny lewy wykres: odwrotność wielkości podaży kapitału jako dodatnio nachyloną funkcję ceny kapitału. Górny, lewy wykres: przekłada tę cenę na, dla danego r, na stopę procentową w postaci wykresu - hiperboli równoosiowej: p_K = r/i. Dolny wykres: cena kapitału razy wielkość kapitału, E_K =p_KK, z górnego lewego rogu na stopę procentową z prawego górnego rogu. Na przykład porównujemy p_K² > p_K¹ wzdłuż krzywej podaży. Ponieważ ma ona nachylenie dodatnie, K₂ jest większe od K₁ oraz p_K²K₂ jest większe od p_K¹K₁. Jednakże wzdłuż hiperboli równoosiowej i₂ jest mniejsze od i₁ jeżeli p_K² > p_K¹. Tak więc E_K² musi być większe od E_K¹ jeżeli i₂ jest mniejsze od i₁ i jeżeli krzywa wydatków ma nachylenie ujemne.

Równowaga ogólna na rynku kapitałowym

Funkcja E_K(i) nie jest funkcją popytu w zwykłym znaczeniu. Oczywiście można argumentować, że jeżeli stopa procentowa obniża się, to pewne przedsięwzięcia inwestycyjne, które były nieopłacalne, stają się opłacalne i firmy zgłoszą większe zapotrzebowanie na fundusze inwestycyjne. Problem polega na tym, że równanie: r = i • DPV_T pokazuje jasno, że stopy procentowej nie można określić niezależnie od ceny kapitału w równowadze w LR. Lepsze podejście polega na spostrzeżeniu, że w równowadze w LR na rynku doskonale konkurencyjnym, cena kapitału = LRMC jego wyprodukowania. Ilość wytworzonego kapitału reprezentuje równowagę na obydwu rynkach: produkcyjnym (gdzie wielkość podaży kapitału = wielkości popytu przy LRMC: p_K^e wyprodukowania tej ilości) i na rynku funduszy pożyczkowych. (Wydatki na inwestycje, E_K(i_e) równają się wielkości oszczędności konsumentów, S(i_e) przy stopie procentowej w równowadze, i_e). W LR stawka wynajmu kapitału w równowadze wyznaczana jest więc przez cenę kapitału w równowadze w LR oraz przez stopę procentową w równowadze. Jest to rozwiązanie dla r równania:

DPV = r/i = p_K, czyli:

r_e = i_ep_K^e.

Kapitał ludzki i popyt na wykształcenie

Przedstawiony model rynku kapitałowego można wykorzystać do wyjaśnienia, w jaki sposób decyzje inwestycyjne są podejmowane. Zawsze, gdy trzeba dokonać płatności dzisiaj aby otrzymać strumień korzyści w przyszłym okresie mamy do czynienia z dobrem o cechach charakterystycznych podobnych do dobra kapitałowego. Przykładem takiego dobra jest wykształcenie umożliwiające jednostce akumulację kapitału ludzkiego. Zdobywanie wykształcenia wymaga ponoszenia dwóch rodzajów wydatków. Po pierwsze, oczywiste koszty nabycia książek i zapłacenia czesnego. Po drugie, zdobywanie wykształcenia właściwie zawsze wymaga pewnego ograniczenia czasu poświęconego na pracę. Niektórzy studenci rezygnują z pracy w ogóle w czasie studiów. A więc pojawia się pośredni koszt w postaci nie zarobionych pieniędzy. Są to tzw. koszty alternatywne wykształcenia.

Zdyskontowana wartość bieżąca wykształcenia

Jako korzyść z ponoszonych wydatków absolwenci oczekują, że zarobią wyższy dochód w ciągu swego życia. Ale te korzyści w postaci większych dochodów pojawią się w przyszłości, a koszty na kształcenie trzeba ponieść dzisiaj. Aby dodatkowe dochody co najmniej pokryły koszty edukacji, DPV dodatkowych dochodów musi być większa (lub równa) całkowitym kosztom kształcenia:

c_d - koszty bezpośrednie (odpowiednio obliczone)

c_o - koszty alternatywne (odpowiednio obliczone)

M₂ - roczny dochód z wykształceniem

M₁ roczny dochód bez wykształcenia.

Możemy teraz przedstawić DPV czteroletnich studiów jako różnicę między DPV rocznych dochodów z wykształceniem i bez niego. Dodatkowo DPV dochodu z wykształceniem musi być zdyskontowana z przesunięciem o 5 lat:

.

W równowadze w LR na rynku kapitałowym doskonale konkurencyjnym, gdy wszystkie jednostki mogą zaciągnąć pożyczki w wysokości pełnego kosztu edukacji, DPV edukacji musi równać się kosztowi:

DPV = c_d + c_o.

Rozszerzenie podstawowego modelu

W bardziej realistycznej wersji tego modelu możemy przyjąć, że dochody mogą zmieniać się z roku na rok w obu sytuacjach (z wykształceniem i bez niego) i stopa zmian może być różna. Np. bez wykształcenia dochody mogą rosnąć szybko osiągając swój szczyt szybko na względnie niskim poziomie. W takim przypadku obliczanie DPV musi być robione dla każdego roku osobno. Niech więc r_t będzie dodatkowym dochodem uzyskanym dzięki zdobyciu wykształcenia w roku t. DPV obliczana jest zgodnie z formułą:

,

gdzie T oznacza przejście na emeryturę. Dodatkowo należy uwzględnić, że bezpośrednie koszty wykształcenia ponoszone są przez kilka lat i dlatego również powinny być zdyskontowane.

Eksploatacja nieodnawialnych zasobów naturalnych

Model rynku kapitałowego może być również wykorzystywany do analizy optymalnego sposobu eksploatacji nieodnawialnych zasobów naturalnych, jak np. ropa naftowa. Nieodtwarzalne zasoby znajdujące się w ziemi mają ekonomiczną charakterystykę podobną do kapitału lub pieniędzy w banku. Wydobycie zasobów dzisiaj oznacza, ze nie będzie ich można wydobyć jutro. Pozostawienie ich w ziemi jest analogią do posiadania pieniędzy w banku. Dzisiaj mamy wybór. Jeżeli wszystkie wydobędziemy dzisiaj, to możemy „zdeponować je w banku po rynkowej stopie procentowej”. W równowadze jeżeli wszystkie nieodnawialne zasoby są własnością prywatną i zostają sprzedane na rynku doskonale konkurencyjnym, to kwota, jaką można zarobić pozostawiając zasoby w ziemi musi równać się przychodom, jakie można zarobić ze sprzedaży zasobów i złożenia pieniędzy w banku. Oznacza to, że przychody z wydobycia wszystkiego dzisiaj muszą równać się DPV przychodów z wydobycia jutro.

Jeżeli:

p₀ - cena rynkowa zasobów dzisiaj,

p₁ - cena rynkowa zasobów jutro

LRMC - LRMC wydobycia,

to zależność między wydobyciem dzisiaj i wydobyciem jutro można zapisać w postaci:

.

Renta z zasobów

Różnica między ceną dzisiaj i kosztem krańcowym wydobycia określana jest mianem kosztów alternatywnych wydobycia dzisiaj zamiast pozostawienia ich w ziemi. Można ją również interpretować jako rentę ekonomiczną zasobu pozostawionego w ziemi (wartość samego zasobu). W przeciwieństwie do wyprodukowanych dóbr (gdy cena równa się MC w równowadze w LR) w odniesieniu do obecnie eksploatowanego zasobu, cena przewyższa LRMC eksploatacji o wartość jednostkową zasobu pozostającego w ziemi.

Analogicznie do przychodów w następnym okresie, które muszą być dyskontowane aby sprowadzić ich wartość do okresu bieżącego, przychody okresu 2 (i każdego następnego) muszą być odpowiednio zdyskontowane:

.

Po przekształceniu wyrażeń otrzymujemy:

.

Z powyższego równania wynika, że w każdym momencie (oczekiwana ) cena musi równać się LRMC powiększonym o koszty alternatywne. Inaczej mówiąc, jednostkowa renta ekonomiczna rośnie zgodnie ze stopą procentową w miarę eksploatacji zasobu.

Substytucja zasobów

Jeżeli popyt na zasób ma nachylenie ujemne, to przy wzroście ceny wraz z upływem czasu wielkość popytu maleje. Jeżeli krzywa popytu ma punkt przecięcia „cenowy”, to wielkość popytu spada do zera. To mogłoby się zdarzyć, gdyby istniały bliskie substytuty zasobu i mogłyby być wykorzystane, gdy jego cena byłaby zbyt wysoka.

Rys. 18.11: lewa część pokazuje wielkość popytu w różnych momentach czasu przy wzroście ceny. Cena i wielkość (p₁, q₁) w czasie 1, (p₂, q₂) w czasie 2, (p₃, q₃) w czasie 3. Prawy wykres porównuje wielkości popytu wzięte z lewego wykresu q₁ w czasie 1, q₂ w czasie 2, q₃ w czasie 3. Wielkości wydobycia maleją wraz z upływem czasu w końcu osiągając 0, pomimo że w dalszym ciągu mogą istnieć złoża dostępne do eksploatacji. Jeżeli powstaną nowe źródła podaży, to krzywa pokazująca wielkości wydobycia ulegnie przesunięciu od początku układu współrzędnych.

Ważnym zastosowaniem tego modelu jest uświadomienie, że ludzkość nie wyeksploatuje wszystkich złóż. Jeżeli nowe zasoby nie zostaną odkryte, cena wzrośnie aż nowe substytuty stają się względnie niedrogie i zastępują pierwotny surowiec. Na przykład przed XVI wiekiem węgla prawie nie wykorzystywano. Uważano go za gorszy surowiec w porównaniu do węgla drzewnego. W XVI w. cena węgla drzewnego wzrosła w Anglii znacząco gdyż wyeksploatowano lasy i nie zadbano o nasadzenie nowych.

Odnawialne zasoby naturalne - drzewa

W przypadku nieodnawialnych zasobów istnieje pewna stała podaż, którą ewentualnie mogą zwiększyć odkrycia w przyszłości. Odnawialne zasoby zwiększają się w tempie określonym przez procesy biologiczne i mogą być eksploatowane w sposób dyskretny lub ciągły. W przypadku lasów mówimy o drzewach, które osiągają wiek do ścięcia, natomiast w przypadku rybołówstwa mówimy o zasobie, który ciągle rodzi się i umiera. Połowy dokonywane są w określonych wielkościach umożliwiając odnawianie się biologiczne ryb.

Stopa wzrostu drzew

Mamy funkcję x(t) opisującą zasób drewna osiągalny w każdej chwili. Typowy biologiczny wzrost przedstawia krzywa S (rys. 18.12). Początkowo wzrost jest gwałtowny, a potem maleje aż las „napełni się”. Górną granicą ilości drewna w lesie jest
. Pochodną względem czasu funkcji x(t) można zapisać w postaci:

,

która jest dodatnia i wklęsła. Z rysunku wynika, że stopa wzrostu początkowo rośnie, potem maleje aż w końcu osiąga zero w
(rys. 18.13)

Optymalny czas zbiorów

Aby określić optymalny czas dokonania wyrębu lasu należy problem rynku kapitałowego przekształcić w problem uwzględniający ciągły upływ czasu aby obliczyć pochodną względem t i wyznaczyć t*. W podejściu dyskretnym, dla danej nominalnej stopy procentowej, czynnikiem dyskontującym jest: 1/(1 + i)^t. Dla tej samej stopy procentowej czynnikiem dyskontującym w podejściu ciągłym jest: e^-it. Jeżeli więc pomijamy MC uprawy i cena sprzedaży wynosi p, to możemy wyrazić DPV zasobu drewna w czasie t jako cenę pomnożoną przez ilość dostępnego drewna odpowiednio zdyskontowaną:

V(t) = px(t)e^-it.

Aby określić optymalny czas wyrębu maksymalizujemy V(t) wybierając t:

.

Po wstawieniu
do powyższego równania:

.

Rozwiązanie dla f(x(t*)): f(x(t*)) = ix(t*).

Tę optymalną decyzję przedstawia rys. 18.14. Przy x na osi poziomej, ix jest funkcją liniową o nachyleniu i. Dzięki optymalnej decyzji drzewa rosną tak długo, aż stopa wzrostu jest większa od iloczynu zasobu drewna i stopy procentowej. Drzewa są wycinane, gdy zasób drewna wynosi x(t*) rosnąc w tempie f(x(t*)).

Statyka porównawcza wzrostu stopy procentowej

Wzrost stopy procentowej oznacza wzrost kosztu czekania na wyrąb i powinien prowadzić do szybszego wyrębu mniejszego zasobu drewna.

Rys. 18.15: i₁ ↑ i₂ ⇒ rośnie nachylenie funkcji ix, co prowadzi do wzrostu punktu przecięcia f(x) przy mniejszym zasobie drewna, x₂ < x₁.

Optymalne zarządzanie rybołówstwem

Zakładamy, ze zasoby ryb są własnością prywatną i ryby są sprzedawane na rynku doskonale konkurencyjnym. Zaczynamy od krzywej biologicznego wzrostu przyjmując, że zasoby same odtwarzają się. Porównujemy ilość ryb dostępnych do połowu z ilością zwiększającą zasób w każdym roku. Daje nam to ilość do połowu przy utrzymaniu zasobu na zadanym poziomie. Jest to funkcja odnawialnej wydajności (sustainable-yield function) - rys. 18.16.

Jeżeli zasób ryb, F, jest bardzo mały, to wydajność, Y, również jest mała. Przy pewnej wielkości zasobu największa ilość ryb jest do niego dodawana i jednocześnie odławiana. Jest to tzw. maksymalna odnawialna wydajność, MSY (maximum sustainable yield). Jeżeli zasób zwiększa się wydajność maleje ze względu na zatłoczenie. Przy odpowiedniej wielkości zasobu ilość nowych ryb równa się wielkości odłowu.

Przychody odnawialne (sustainable revenues) - rys. 18.17

Przyjmijmy, że ilość ryb do odłowienia jest proporcjonalna do zasobu ryb (czyli im więcej ryb tam jest, tym więcej można odłowić) i wysiłku. Ryby sprzedawane są na rynku doskonale konkurencyjnym, czyli po stałej cenie niezależnej od wielkości połowów.

Przy produkcie proporcjonalnym do zasobu i stałej cenie, funkcja odnawialnej wydajności określa kształt funkcji określającej odnawialne przychody, które można uzyskać dzięki odpowiedniemu zarządzaniu rybołówstwem. Przy zwiększaniu połowów z roku na rok, początkowo odnawialna wydajność rośnie prowadząc do wzrostu odnawialnych przychodów. Po przekroczeniu maksimum przez odnawialną wydajność, odnawialne przychody zaczynają maleć.

Efektywna stopa połowów

Przy efektywnej stopie połowów maksymalizujemy zdyskontowane zyski. Należy więc znaleźć maksimum odnawialnych zysków. Zaczynamy od określenia odpowiedniej, zdyskontowanej funkcji kosztów.

Rys. 18.18: wyznaczenie efektywnego poziomu połowów dla odpowiedniej LRTC liniowej: C*, gdy nachylenie LRTC = nachyleniu funkcji odnawialnych całkowitych przychodów, STR. Maksimum odnawialnych zysków wynosi więc:

Sπ* = STR(C*) - LRTC • C*,

Z rysunku wynika, że efektywna wielkość połowów zawsze jest mniejsza od maksymalnej odnawialnej wydajności w każdym roku dla dodatnich LRMC. Jest to najważniejszy wniosek ekonomiczny. Jest on podobny do spostrzeżenia, że monopolista zawsze znajduje się na elastycznej części krzywej popytu. Wniosek w obu przypadkach: przy dodatnich MC maksymalizacja zysku nie pokrywa się z maksymalizacją przychodów.

Statyka porównawcza wzrostu stopy procentowej

Po wyznaczeniu optymalnej wielkości połowów, warto zbadać wpływ na nią wzrostu stopy procentowej. Wzrost ten ma wpływ na DLRTC sprzeczny z intuicją. Jednym ze składników jest koszt alternatywny zwiększenia połowów dzisiaj. Jest to analogia do zwiększenia wydobycia nieodnawialnych zasobów dzisiaj. Jeżeli stopa procentowa rośnie, to koszty alternatywne szybszej eksploatacji zasobów maleją. Dzieje się tak, gdyż zyski zarobione dzisiaj i zdeponowane w banku zgodnie z rynkową stopą procentową mogą zarobić więcej przy wzroście stopy procentowej. Zmniejszenie się kosztów alternatywnych zwiększenia połowów dzisiaj implikuje zmniejszenie DLRMC przy niezmienionym rzeczywistym koszcie połowów.

Rys. 18.19: skutek zmniejszenia DLRTC: krzywa kosztów całkowitych przesuwa się do dołu i wielkość połowów dzisiaj rośnie. TC₁ ↓ TC₂ ⇒ C₁* ↑ C₂*: spadek stopy procentowej = wzrost efektywnej stopy połowów.

Ekonomiczna interpretacja liczby e

Startując od kapitału $1 deponujemy go w banku ze stopą procentową = 100% rocznie.

V(1) = kapitał początkowy (1 + stopa procentowa)

= 1(1 + 100%) = (1 + 1/1)¹ = 2

Funkcja:
, jeżeli m (częstotliwość kapitalizacji) dąży do nieskończoności, to V(m) dąży do 2,71828... = e, czyli:

.

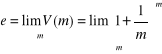
Liczba e może być interpretowana jako wartość, do jakiej wzrośnie po roku kapitał początkowy o wartości $1, gdy odsetki przy stopie procentowej równej 100% rocznie będą kapitalizowane w sposób ciągły.

Ciągły proces kapitalizacji odsetek można uogólnić w trzech kierunkach:

1. więcej lat kapitalizacji;

2. kapitał początkowy inny niż $1;

3. nominalna stopa procentowa inna niż 100%.

Ciągła kapitalizacja odsetek

Kapitał w $	Nominalna stopa procentowa	Lata ciągłej kapitalizacji	Wartość depozytu na końcu procesu kapitałowego w $
1	100% = 1	1	e
1	100%	t	e^t
A	100%	t	Ae^t
A	r	t	Ae^rt

Problem przechowywania wina

Pewien kupiec ma beczkę wina, którą może sprzedać teraz (t = 0) za sumę $K albo przechowywać przez pewien okres, a potem sprzedać po wyższej cenie. Wiadomo, ze rosnąca wartość wina (V) jest następującą funkcją czasu:
. Jeśli t = 0, to V = K. Kiedy kupiec powinien sprzedać wino aby maxπ przy założeniu, że koszty magazynowania = 0 ?

Maxπ = maksymalizacja przychodów ze sprzedaży, czyli V.

Zał.: r to stopa procentowa przy ciągłej kapitalizacji: wartość bieżąca V:

A(t) = Ve^-rt =
,

gdzie A oznaczające wartość bieżącą V samo jest funkcją t. Musimy więc znaleźć wartość maksymalizującą A.

Warunek pierwszego rzędu: dA/dt = 0, czyli:

.

Ponieważ A ≠ 0, warunek dA/dt = 0 może być spełniony wtedy i tylko wtedy, gdy:

½ t^-1/2 = r, czyli 1/2t^1/2 = r, czyli 1/2r =t^1/2.

Optymalny czas przechowywania:

;

jeśli np. r = 0,1, to kupiec powinien przechowywać beczkę z winem przez 25 lat.

Warunek pierwszego rzędu, 1/2t^1/2 = r, ma łatwą interpretację ekonomiczną. Wyrażenie po lewej stronie reprezentuje stopę wzrostu wartości wina, V:

.

Wyrażenie po prawej stronie jest stopą procentową lub stopą wzrostu przy ciągłej kapitalizacji takiej sumy pieniędzy, jaką można by otrzymać, gdyby udało się sprzedać wino natychmiast. Dla zagadnienia przechowywania wina jest to koszt alternatywny.

Zatem przyrównanie tych dwóch stóp oznacza próbę magazynowania wina dopóty, dopóki zyski z przechowywania wina nie zniknął zupełnie, tzn. czekania do momentu. Gdy malejąca stopa wzrostu wina nie zrówna się ze stałą stopą procentową uzyskaną ze sprzedaży.

Następnym krokiem jest sprawdzenie, czy wartość
spełnia warunki drugiego rzędu dla maksymalizacji A. Druga pochodna jest równa:

.

Ponieważ ostatni składnik znika, gdy obliczamy wartość drugiej pochodnej w punkcie równowagi, gdzie dA/dt = 0, więc pozostaje nam:

.

Ponieważ A > 0, to wartość drugiej pochodnej obliczona w punkcie
> 0 jest ujemna, co upewnia nas, że rozwiązanie
jest rzeczywiście wartością maksymalizującą zysk.

Zagadnienie wyrębu lasu

Zał.: wartość lasu jest następującą funkcją czasu:

(w tysiącach dolarów).

Należy wyznaczyć optymalny termin wyrębu lasu przy założeniach, że stopa dyskontowa jest równa r (ciągła) i podczas wzrostu lasu nie są ponoszone żadne koszty. Najpierw V sprowadzamy do jej wartości bieżącej:

.

Aby zmaksymalizować A musimy ustalić dA/dt = 0. Pierwszą pochodną otrzymujemy różniczkując lnA względem t i następnie mnożąc przez A:

zatem:
.

Ponieważ A ≠ 0 warunek dA/dt = 0 może być spełniony wtedy i tylko wtedy, gdy:

czyli:
.

W konsekwencji optymalna liczba lat wzrostu lasu jest równa:
.

Z rozwiązania wynika, że im wyższa jest stopa dyskontowa, tym wcześniej należy dokonać wyrębu lasu.

Aby upewnić się, że
jest rozwiązaniem maksymalizującym (a nie minimalizującym) trzeba sprawdzić warunek drugiego rzędu.

W tym przykładzie abstrahowaliśmy od kosztów sadzenia lasu i wykluczyliśmy koszty „utopione”. Jeśli decyzja dotyczy problemu, czy w ogóle sadzić las, to koszty sadzenia (poniesione obecnie) muszą być porównane z obecną wartością produkcji drewna, obliczoną dla t ustalonego na poziomie optymalnym
. Np. jeśli r = 0,05, to mamy:

=(0,6931/0,1)² = 48 lat

oraz:

= 2^6,931e^{-0,05 • 48} = 11,0674 tys. dolarów;

zatem jedynie koszty sadzenia mniejsze niż
- przy założeniu, że koszty uprawy = 0 - uczynią przedsięwzięcie wartym zachodu.

7

---