Filip Nowak
Drgania harmoniczne
POLITECHNIKA ŁÓDZKA
WYDZIAŁ MECHANICZNY
ŁÓDŹ 2010
SPIS TREŚCI:
Ruch harmoniczny prosty
Każdy ruch powtarzający się w regularnych odstępach czasu nazywany jest ruchem okresowym. Jeżeli ruch ten opisywany jest sinusoidalną funkcją czasu to jest to ruch harmoniczny. Ciało porusza się ruchem harmonicznym prostym, jeżeli znajduje się pod wpływem siły o wartości proporcjonalnej do wychylenia z położenia równowagi i skierowanej w stronę położenia równowagi:
![]()
gdzie
![]()
- siła
![]()
- współczynnik proporcjonalności
![]()
- wychylenie z położenia równowagi
Równanie ruchu (skalarne dla kierunku OX) dla takiego ciała można zapisać (z II zasady dynamiki Newtona) jako:
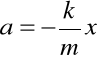
albo w postaci różniczkowej:

Jest to równanie różniczkowe zwyczajne drugiego rzędu (występuje druga pochodna położenia x(t)).
Rozwiązania tego równania można równoważnie opisać za pomocą dowolnej z poniższych funkcji:
gdzie:
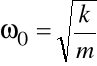
jest częstością kołową drgań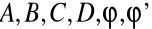
stałe zależne od warunków początkowych
Są to tzw. harmoniki. Rozwiązania są równoznaczne, a korzystając z tożsamości trygonometrycznych można znaleźć zależności pomiędzy powyższymi stałymi i rozwiązanie przedstawiać w dowolnej z postaci 1,2,3.
Częstość kołową ω0 wiąże z okresem drgań T związek:
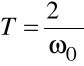
częstotliwość drgań ν natomiast wynosi
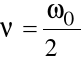
Energia w ruchu harmonicznym prostym
Energia potencjalna dla siły proporcjonalnej do wychylenia.
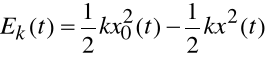
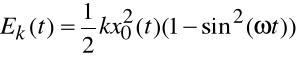
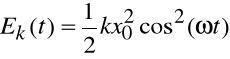
Z równania powyższego wynika kilka faktów (na podstawie jedynki trygonometrycznej i porównania współczynników we wzorze 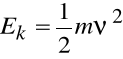
z powyższym):
Ciało drgające ma maksymalną prędkość, gdy przechodzi przez położenie równowagi i ma ona wartość:
![]()
prędkość chwilowa zmienia się jak
![]()
Bezpośrednio z równania ruchu wynika, że przyspieszenie jest opisywane zależnością:
![]()
Wykres zależności energii od wychylenia
Ruch harmoniczny tłumiony
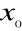
- położenie początkowe, dla t = 0,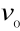
- prędkość początkowa, dla t = 0.Oscylator drgający
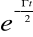
- malejąco z wykładnikiem czasu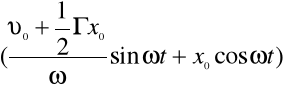
- oscylacyjnego, zmieniającego się z częstością ωOscylator przytłumiony
Przybliżanie innych rodzajów ruchów przez drgania harmoniczne
|
Ruch harmoniczny tłumiony występuje wtedy, gdy na ciało działa dodatkowo siła oporu ośrodka proporcjonalna do prędkości:
![]()
Równanie ruchu ma wtedy postać:
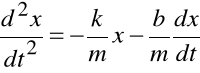
Wprowadzając oznaczenie:
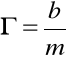
Powyższe równanie można wyrazić:
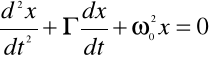
Rozwiązanie równania można wyrazić w postaci:
![]()
Przy czym przyjęto oznaczenie:
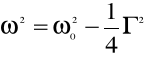
Wielkość ω jest nazywana zmodyfikowaną częstością drgań, jest zależna nie tylko od siły kierującej ale też od współczynnika tłumienia i maleje gdy współczynnik tłumienia rośnie.
Stałe A i B zależą od warunków początkowych następującymi związkami:
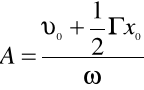
![]()
gdzie:
Gdy 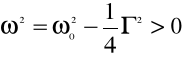
, jest liczbą liczbą rzeczywistą. Ruch opisuje wzór:
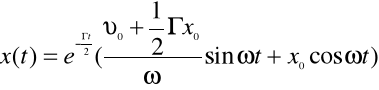
Przedstawione wyżej rozwiązanie składa się z dwóch czynników:
Dla słabego tłumienia czynnik wykładniczy jest w ciągu jednego cyklu w zasadzie stały, co można uwzględnić w obliczeniach. Wówczas można przyjąć, że ruch jest harmoniczny, z malejącą amplitudą.
Gdy tłumienie jest silne 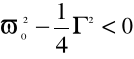
, wówczas ω nie ma wartości rzeczywistych. Ale przyjmując, że jest wartością urojoną powyższe równanie spełnia rozwiązanie. Przyjmując:
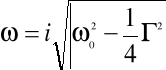
Po wykorzystaniu własności funkcji trygonometrycznych dla wartości urojonych, rozwiązanie można zapisać w postaci:
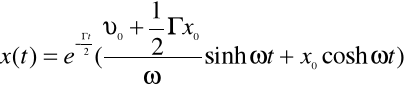
Przypadek ten odpowiada tak zwanemu oscylatorowi przetłumionemu. W tej sytuacji drugi czynnik wyrażenia jest wolnozmienny a nie oscylacyjny jak poprzednio, dlatego nie występuje ruch wahadłowy, a jedynie zbliżony do eksponencjalnego zanik wychylenia z czasem.
Przybliżenie za pomocą prostego ruchu harmonicznego stosuje się np. do opisu małych drgań wahadła matematycznego.
Ogólniej, załóżmy, że ciało znajduje się w położeniu xr równowagi trwałej; innymi słowy w punkcie xr energia potencjalna tego ciała przyjmuje wartość minimalną E(xr). Jeżeli funkcja E(x) posiada rozwinięcie w szereg Taylora w otoczeniu xr, otrzymujemy:
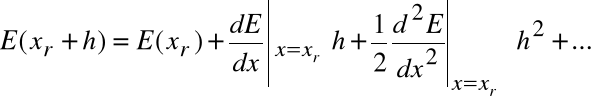
Dla dostatecznie małych h można pominąć wyrazy z h do potęgi większej niż 2. Wyraz z h się zeruje (warunek konieczny występowania minimum), pozostaje równanie postaci:
![]()
Można obliczyć siłę dla takiej energii potencjalnej jako ujemny gradient potencjału (energii potencjalnej).
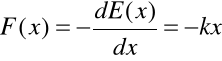
Wniosek: Pod warunkiem, że dla danego ruchu funkcja energii E(x) jest funkcją dość regularną (tzn. posiada rozwinięcie w szereg Taylora, co w praktyce oznacza, że posiada ciągłą pierwszą i drugą pochodną w pewnym otoczeniu punktu równowagi) to dla niewielkich wychyleń z położenia równowagi ruch ten możemy opisywać z dobrym przybliżeniem jako drgania harmoniczne.
8
Ep+Ek
Ep
Ek
0
0,5
-0,5
1
0
-1
-0,1
0,1
0,2
0,3
0,4
0,5
0,6
Wyszukiwarka
Podobne podstrony:
Drgania harmoniczne strun, 1. WST˙P.
F12 drgania harmoniczne
WAHADLO1, MIBM WIP PW, fizyka 2, laborki fiza(2), 9-Drgania harmoniczne tłumione w układach mechanic
DRAGANIA WYMUSZONE, DRAGANIA WYMUSZONE- przy wymuszeniu harmonicznym w układzie ustalają się drgani
Drgania harmoniczne struny, Struna 1, POLITECHNIKA ŚLĄSKA
ćw.01 - Drgania harmoniczne sprężyny, konspekt, Nr ćwiczenia
Fizyka - drgania harmoniczne, szkola, Fizyka
Lab 9, MIBM WIP PW, fizyka 2, laborki fiza(2), 9-Drgania harmoniczne tłumione w układach mechaniczny
bud mechanika budowli 03 drgania harmoniczne
Drgania harmoniczne sprężyny, AGH WIMiC, Rok I, Fizyka, Laboratoria, Ćwiczenie 1
ćw.01 - Drgania harmoniczne sprężyny, Drgania harmoniczne sprężyny, Nr ćwiczenia: 1
wahadlo2, Proste drgania harmoniczne: wahad³o matematyczne i fizyczne
Drgania harmoniczne struny, Drgania harmoniczne struny 1, Politechnika ˙l˙ska
drgania harmoniczne struny
Drgania harmoniczne struny, Drgania harmoniczne struny 4, Wydzia˙: AEI
091, MIBM WIP PW, fizyka 2, laborki fiza(2), 9-Drgania harmoniczne tłumione w układach mechanicznych
Drgania harmoniczne sprężyny, studia, fizyka
drgania harmoniczne struny
Drgania harmoniczne
więcej podobnych podstron