Nr ćwiczenia: 106	Data: 08-05-2001r.	Marek Frątczak		Wydział Elektryczny	Semestr II	Grupa: E-9
Prowadzący: mgr Jarosław Gutek			Przygotował: Marek Frątczak	Wykonał: Marek Frątczak	Opracował: Marek Frątczak	Ocena:

Temat: Wyznaczanie współczynnika przewodnictwa cieplnego metali.

1. Wstęp teoretyczny.

Przewodnictwo cieplne polega na przekazywaniu ciepła od pewnego elementu ciała do elementów sąsiednich poprzez przekazywanie energii kinetycznej bezładnego ruchu cieplnego od jednych drobin do drugich w wyniku zderzeń.

W naszym ćwiczeniu bierzemy pod uwagę element pręta o powierzchni przekroju A i długości dx, którego powierzchnie zewnętrzne utrzymywane są w stałych, ale różnych temperaturach.

Strumień ciepła
, który przepływa przez przekrój pręta określamy jako stosunek ilości ciepła do czasu:

(I)

Podstawowe prawo przewodnictwa cieplnego mówi, że strumień ciepła jest proporcjonalny do powierzchni przekroju i do różnicy temperatur na odcinku dx

(II)

nazywamy współczynnikiem przewodnictwa cieplnego, mierzymy go
;
i jest to gradient temperatury.

Jeżeli pręt ma stały przekrój i jest doskonale izolowany, to

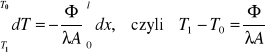
(III)

Z tego równania możemy łatwo odczytać znaczenie współczynnika przewodnictwa cieplnego. Gdy
jest duże, wówczas na utrzymanie stałej różnicy temperatur
trzeba dostarczyć duży strumień ciepła. W przeciwnym przypadku przekazywanie ciepła do zimnego końca jest powolne - do podtrzymania różnicy temperatur wystarczy mały strumień dostarczanego ciepła.

Rozkład temperatury wzdłuż pręta otrzymamy całkując równanie (II) od dowolnego punktu (temp. T) do końca pręta (x = l,
). Wykorzystując przy tym równanie (III) otrzymujemy:

(IV)

Z powyższego równania (IV) otrzymujemy opis rozkładu temperatury wzdłuż pręta tylko wtedy, gdy jest on dobrze izolowany.

Podczas, gdy powierzchnia boczna nie jest izolowana cieplnie, strumień przepływający przez kolejne powierzchnie jest coraz mniejszy czego efektem jest ucieczki ciepła do otoczenia. Biorąc pod uwagę, że strumień ciepła przez ściany boczne jest proporcjonalny do różnicy temperatur między danym punktem a otoczeniem (prawo ostygania) można otrzymać równanie opisujące rozkład temperatury w tym przypadku w postaci:

, (V)

gdzie h jest stałą charakteryzującą pręt i ośrodek zewnętrzny.

Prawo Wiedemanna - Franza -wyraża stosunek przewodnictwa cieplnego
do przewodnictwa elektrycznego
jest proporcjonalny do temperatury i nie zależy od rodzaju ciała

.

W celu wyznaczenia współczynnika cieplnego metali stosujemy układ pomiarowy przedstawiony na poniższym rysunku.

2. Opis przeprowadzonego ćwiczenia.

• Mierzę odległość między punktami pomiaru temperatury oraz średnicę pręta

• Łączę obwód grzejnika i termopary według rysunku, następnie wypełniam naczynie wodą z lodem

• Włączam grzejnik ustawiając odpowiednie napięcie i czekam na ustalenie się temperatury. W odstępach 5-10 minutowych dokonuję pomiary temperatury w kilku punktach pręta, notując wartości w tabelce. Przepływ uznaję za ustalony, jeżeli kolejny pomiar wykaże wartości bliskie poprzedniego dla wszystkich punktów

• Wykreślam zależność temperatury w pręcie od odległości.

• Z nachylenia wykresu dla stanu równowagi szukam gradientu temperatury (dt/dx) stosując regresję liniową

• Obliczam współczynnik przewodnictwa cieplnego

3. Dane eksperymentalne.

Tabela z dodatkowymi danymi:

η - sprawność grzejnika z:		R [mm] - promień rurki z:		Odległość między punktami pomiarowymi [mm]:
aluminium	mosiądzu	aluminium	Mosiądzu
10 0,1	10 0,1	0,52 0,01	0,24 0,01	50 2

Tabela z pomiarami z ćwiczeniu:

Napięcie i natężenie	60 V, 165 mA		65 V, 179 mA
x [mm]	Temperatura ^oC			Temperatura ^oC
		aluminium	Mosiądz		Aluminium	mosiądz
0	24,9	26,0		26,4	27,0
50	22,8	23,0		24,0	23,5
100	19,8	20,5		20,8	20,9
150	16,9	17,4		17,7	17,5
200	14,1	14,1		14,8	14,3

Tabelka dla strumienia ciepła -
:

L.p. Rodz. rurki	1	2
aluminiowa	5,18	6,08
mosiężna	2,39	2,81

Tabelka dla gradientu temperatury:

L.p.	aluminium	mosiądz
1	-55	-58,8
2	-59	-62,8

Przekrój prętów jest równy:

A=314,16[mm²]

Tabelka dla współczynnika przewodnictwa cieplnego - α:

L.p.	λ
	aluminium	mosiądz
1	299,8	129,4
2	352,1	142,4

4. Przykładowe obliczenia.

• Obliczanie strumienia cieplnego -
  :

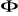
[W].

• Obliczanie gradientu temperatury -
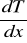
  na podstawie regresji liniowej.

• Obliczanie współczynnika przewodnictwa cieplnego - λ:

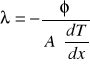
5. Dyskusja błędów.

• Obliczanie błędów strumienia za pomocą różniczki zupełnej:

materiał	aluminium		mosiądz
[W]	0,059	0,064	0,027	0,029

Dla:
;

• Obliczanie błędu dla przekroju A:

dla

Z tego wynika, że

• Obliczanie błędu dla współczynnika przewodnictwa cieplnego -
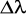
  z różniczki zupełnej:

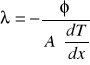
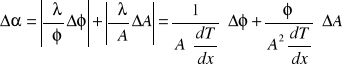
L.p.	aluminium	mosiądz
1	11,83	34,53
2	38,37	53,54

6. Wnioski.

W doświadczeniu mieliśmy do czynienia z prętami: aluminiowy i mosiężny, które to były izolowane cieplnie od otoczenia .W doświadczeniu zrobiłem pomiary tylko dla dwóch wartości napięć (60 i 65V). Spowodowane to był tym, że na początku ćwiczenia było ustawione zbyt duże napięcie i termopary nagrzały się do wysokiej temperatury. W efekcie do przeprowadzenia ćwiczenia przystąpiłem z dużym opóźnieniem, ponieważ musiałem czekać na schłodzenie się termopar, co trwało kilkadziesiąt minut. Gradient temperatury obliczony został programem p. Szuby. Ze wzrostem odległości od gorącego końca, temperatura zmniejsza się liniowo co przedstawiają wykresy. Wartości współczynników rozszerzalności cieplnej dla aluminium i mosiądzu porównywalne są z wartościami tablicowymi (aluminium 299
; mosiądz 129
). Pobrane pomiary potwierdzają także fakt, iż w ciałach o większym współczynniku przewodnictwa cieplnego przekazywanie ciepła do zimnego końca odbywa się szybciej niż w ciałach o niższym współczynniku przewodnictwa cieplnego. Ustalanie się równowagi cieplnej dla różnych napięć trwało około 15 minut. Dla pręta mosiężnego temperatura w punkcie 1 była zawsze wyższa niż dla aluminium , natomiast na końcu pręta czyli w punkcie 5 temperatura pręta miedzianego była zawsze niższa niż pręta aluminiowego. Wynika z tego, że w pręcie aluminiowym następuje szybciej wymiana ciepła miedzy jego końcami znajdującymi się w różnych temperaturach niż w pręcie mosiężnym.

5

---