Laboratorium Wytrzymałości materiałów	Imię i nazwisko: Kamila Michalska Rok, grupa: UHiP
Numer i temat ćwiczenia: Nr 1. Statyczna próba rozciągania.	Data wykonania: 04/10/2011	Przygotowanie	Sprawozdanie
				Sprawdzian	Ocena:

Własności mechaniczne badanych materiałów odznaczają się takimi cechami jak: sprężystość, plastyczność, lepkość i wytrzymałość.

• Sprężystość jest to zdolność ciała do powrotu do pierwotnych wymiarów i kształtu po usunięciu przyczyn powodujących odkształcenie.

• Plastyczność jest to zdolność ciała do całkowicie nieodwracalnego odkształcenia. Odkształcenie takie, nazywane odkształceniem plastycznym zależy tylko od wartości obciążenia, a nie zależy od czasu działania obciążenia ani od prędkości zmian.

• Lepkość jest to cecha przejawiająca się w postaci sił oporu (tarcia wewnętrznego) przeciw ruchom wewnętrznym ciała, wykazującym przestrzenne zróżnicowanie prędkości.

• Wytrzymałość określa wartość obciążenia konieczna do pokonania sił spójności występujących między poszczególnymi atomami ciała.

Własności mechaniczne badanych materiałów dzielimy na wytrzymałościowe i technologiczne.

• Własności wytrzymałościowe obejmują te wszystkie własności materiału, do których określenia niezbędna jest znajomość siły jako podstawowego parametru (np. umowna granica sprężystości, wyraźna granica plastyczności, wytrzymałość na rozciąganie, naprężenia rozrywające).

• Własności technologiczne, nazywane również plastycznymi, charakteryzują przydatność materiału do odpowiedniej obróbki (np.. do przeróbki plastycznej). Określa się je za pomocą wskaźników, takich jak: wydłużenie względne, wydłużenie równomierne, przewężenie względne.

Ogólnie badane materiały możemy podzielić na plastyczne i kruche.

• Materiałami plastycznymi nazywamy te, które przy rozciąganiu wykazują znaczne odkształcenia trwałe.

• Materiałami kruchymi są takie, które przy rozciąganiu nie wykazują znacznych odkształceń trwałych. Taki podział materiałów jest umowny, pomnie waz ten sam materiał może być plastyczny lub kruchy w zależności od warunków badania (temperatury, prędkości obciążenia, stanu naprężenia).

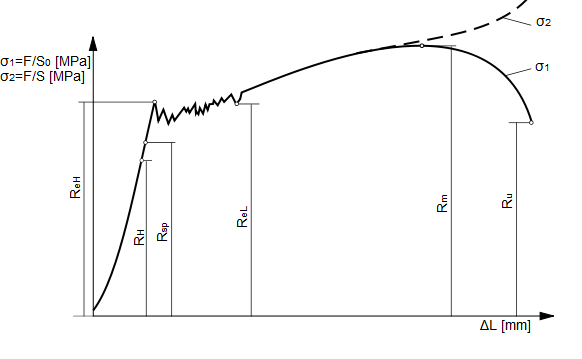
Typowy wykres naprężenie-odkształcenie pokazuje rysunek po prawej. Początkowo wzrost naprężenia powoduje liniowy wzrost odkształcenia. W zakresie tym obowiązuje prawo Hooke'a. Po osiągnięciu naprężenia R_sp, zwanego granicą sprężystości materiał przechodzi w stan plastyczności, a odkształcenie staje się nieodwracalne. Przekroczenie granicy sprężystości, zauważalne w okresie chwilowego braku przyrostu naprężenia, powoduje przejście materiału w stan plastyczny. Dalsze zwiększanie naprężenia powoduje nieliniowy wzrost odkształcenia, aż do momentu wystąpienia zauważalnego, lokalnego przewężenia zwanego szyjką. Naprężenie, w którym pojawia się szyjka, zwane jest wytrzymałością na rozciąganie R_m. Dalsze rozciąganie próbki powoduje jej zerwanie przy naprężeniu rozrywającym R_u.

Umowne odkształcenie ε = (L₁-L₀)/L₀ ,

gdzie L₀- dł. Początkowa próbki, (L₁-L₀) - wydłużenie próbki

Umowne naprężenie σ = F/S₀ ,

gdzie F- siła rozciągania, S₀- pierwotne pole przekroju poprzecznego.

Z wykresu rozciągania możemy odczytać kilka charakterystycznych punktów, zwanych granicami:

• Granicą proporcjonalności - R_H= F_H/S₀ (granica stosowalności prawa Hooke'a) nazywamy największą wartość naprężenia umownego, przy której zachodzi jeszcze proporcjonalna zależność między wydłużeniem i naprężeniem

• Granicą sprężystości - nazywamy największą wartość naprężenia umownego, przy której nie wystąpią jeszcze odkształcenia trwałe

• Umowną granicą sprężystości - R_0,05=F_0,05/S₀ nazywamy taką wartość naprężenia umownego, które wywołuje w próbce wydłużenie trwałe równe 0,05% pierwotnej dł. pomiarowej próbki L₀

• Wyraźna granica plastyczności - R_e= F_e/S₀ jest to takie naprężenie umowne, po osiągnięciu którego występuje wyraźny wzrost wydłużenia rozciąganej próbki bez wzrostu obciążenia; rozróżnia się górną granice plastyczności R_eH i dolną R_eL

• Umowna granica plastyczności - R_0,2 =F_0,2/S₀ jest to takie naprężenie, które wywołuje w próbce umowne wydłużenie trwałe wynoszące 0,2% długości pomiarowej L₀

• Wytrzymałość na rozciąganie - R_m= F_m/S₀ jest to naprężenie odpowiadające największej sile rozciągającej w czasie obciążenia odniesionej do przekroju pierwotnego próbki

Naprężenia rozrywające - R_u =F_u/S_u jest to naprężenie rzeczywiste odpowiadające stosunkowej siły rozciągającej w chwili zerwania próbki do powierzchni przekroju poprzecznego próbki w miejscu zerwania

Podczas badania próbki stali na zerwanie określane są także:

• naprężenie rozrywające, czyli rzeczywista wartość naprężenia w miejscu przewężenia rozciąganej próbki bezpośrednio przed jej zerwaniem (jest to wartość siły powodującej zerwanie w odniesieniu do przekroju zerwanej próbki w jej najwęższym miejscu);

• wydłużenie względne, czyli procentowy przyrost długości zerwanej próbki w stosunku do jej początkowej długości,

• przewężenie względne, czyli procentowe zmniejszenie powierzchni przekroju poprzecznego zerwanej próbki w miejscu zerwania do jej przekroju pierwotnego

Własności technologiczne badanego materiału wyznaczone w próbie rozciągania:

• Wydłużenie względne - jest to stosunek przyrostu długości pomiarowej próbki po jeje zerwaniu do pierwotnej długości pomiarowej próbki:

A = [(L_u-L₀)/L₀] * 100% ,

gdzie L₀ - pierwotna dł. pomiarowa próbki, L_u - dł. po zerwaniu

• Przewężenie względne - jest to zmniejszenie powierzchni przekroju poprzecznego próbki w miejscu zerwania w odniesieniu do powierzchni jej pierwotnego przekroju:

Z= [(S₀-S_u)/S₀] * 100% ,

gdzie S₀ - pole przekroju pierwotnego, S_u - pole po zerwaniu

• Wydłużenie równomierne - wyznaczamy dla próbek o przekroju kołowym :

A_r= [(d₀²-d_r²)/d_r²] * 100% ,

gdzie d₀- początkowa średnica próbki, d_r - średnica próbki po zerwaniu

Stałe sprężystości materiału:

• Moduł Younga (E) - inaczej moduł odkształcalności liniowej albo moduł sprężystości podłużnej (w układzie jednostek SI) - wielkość uzależniająca odkształcenie liniowe ε materiału od naprężenia σ, jakie w nim występuje w zakresie odkształceń sprężystych.

Jednostką modułu Younga jest paskal.

Jest to wielkość określająca sprężystość materiału.

Moduł Younga jest hipotetycznym naprężeniem, które wystąpiłoby przy dwukrotnym wydłużeniu próbki materiału, przy założeniu, że jej przekrój nie ulegnie zmianie (założenie to spełnione jest dla hipotetycznego materiału o współczynniku Poissona υ = 0).

• Współczynnik Poissona (ν) jest stosunkiem odkształcenia poprzecznego do odkształcenia podłużnego przy osiowym stanie naprężenia. Współczynnik Poissona jest wielkością bezwymiarową i nie określa sprężystości materiału, a jedynie sposób w jaki się on odkształca.

Jeżeli w przypadku materiału izotropowego w rozpatrywanym punkcie ciała wyróżnimy kierunek m i jeżeli w tym punkcie m

gdzie: ε - odkształcenie, n - dowolny kierunek prostopadły do m

Jeżeli pręt o średnicy d (lub dowolnym innym charakterystycznym wymiarze, np. szerokości) i długości L zostanie poddany rozciąganiu tak, że wydłuży się o ΔL, to jego średnica zmieni się (zmniejszy się, stąd dla uniknięcia wartości ujemnych współczynnika znak minus we wzorze) o:

• Moduł Kirchoffa - moduł sprężystości postaciowej G = E/2(1+ν)

• Objętościowy moduł sprężystości K = E/

Urządzenia stosowane w próbie rozciągania:

• Zrywarki - do wykonania próby rozciągania

• Tensometr mechaniczny - do pomiaru zmian długości pomiarowej próbki

• Próbki - dzielimy je na okrągłe i płaskie; próbki okrągłe dzielimy na : próbki z główkami do chwytania w szczęki, do uchwytów pierścieniowych i z główkami gwintowymi; natomiast próbki płaskie na te z główkami i bez.

Wyniki pomiarów próby rozciągania:

Rodzaj próbki: próbka okrągła do chwytania w szczęki

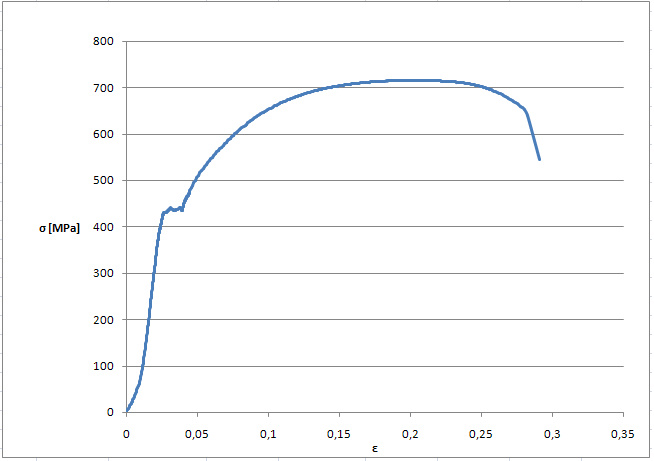
Wykres 1. σ-ε

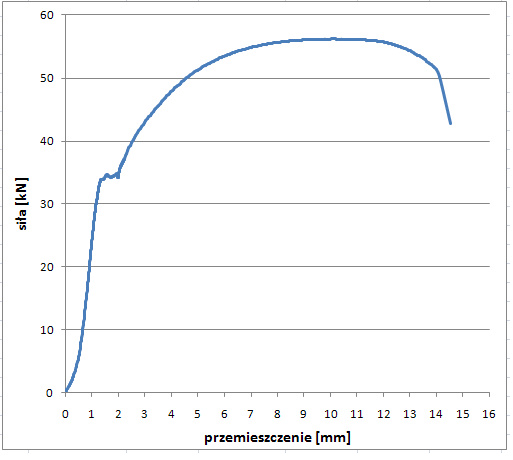
Wykres 2. F-ΔL

L₀=50[mm]

S₀=78,5[mm²]

S_K=50,27[mm²]

R_e=433,026879 [Mpa]

R_m=715,3656051[Mpa

R_z=543,8650955[Mpa] R_z-naprężenie zrywające

R_u=1057,130495[Mpa] R_u-rzeczywiste naprężenie zrywające

Wnioski:

Wykonana przez nas próba rozciągania jest ważna, a na jej podstawie byliśmy w stanie wyznaczyć podstawowe własności wytrzymałościowe i technologiczne badanego materiału. Własności mechaniczne badanych materiałów odznaczają się takimi cechami jak: sprężystość, plastyczność, lepkość i wytrzymałość. Własności mechaniczne materiałów bada się przy obciążeniach statycznych, dynamicznych, zmęczeniowych (wielokrotnie okresowo zmiennych) oraz przy obciążeniach długotrwałych, nie zmiennych w czasie.

Po analizie wykresu można stwierdzić, że z otrzymanego wykresu możemy odczytać wyraźną granicę plastyczności, którą posiada materiał z jakiego wykonano próbkę. Granicę plastyczności określa się dla jednowymiarowego stanu naprężenia (najczęściej przy próbie rozciągania). Dla złożonego stanu naprężenia potrzebne jest odpowiednie kryterium uplastycznienia. Granica plastyczności jest często powiązana z wytrzymałością materiału. Początkowo wzrost naprężenia powoduje liniowy wzrost odkształcenia. W zakresie tym obowiązuje prawo Hooke'a. Po osiągnięciu naprężenia R_sp, zwanego granicą sprężystości materiał przechodzi w stan plastyczności, a odkształcenie staje się nieodwracalne. Przekroczenie granicy sprężystości, zauważalne w okresie chwilowego braku przyrostu naprężenia, powoduje przejście materiału w stan plastyczny. Dalsze zwiększanie naprężenia powoduje nieliniowy wzrost odkształcenia, aż do momentu wystąpienia zauważalnego, lokalnego przewężenia zwanego szyjką. Naprężenie, w którym pojawia się szyjka, zwane jest wytrzymałością na rozciąganie R_m. Wytrzymałość na rozciąganie określana wielkością naprężenia wywołanego w przekroju próbki przez siłę powodującą jej zerwanie. Badane są także inne parametry określające naprężenia w próbkach stali, takie jak wytrzymałość na ściskanie, zginanie, ścinanie i skręcenie..Dalsze rozciąganie próbki powoduje jej zerwanie przy naprężeniu zrywającym R_z. Po za wyliczeniem podstawowych własności materiału przeprowadziliśmy analizę złomu zerwanej próbki, która pozwala nam na określenie budowy krystalicznej materiału. W naszym przypadku mamy do czynienia ze złomem rozdzielczym według opisu zaczerpniętego z literatury. Przeprowadzając analizę symulacji rozciągania próbki z wyraźną granicą plastyczności można zaobserwować, że odciążenia materiału w obszarze plastycznym nie powodują powrotu wzdłuż linii obciążenia, ale wzdłuż prostej odciążenia równoległej do początkowego odcinka krzywej rozciągania.

4

---