CIĄGI LICZBOWE

1.Podstawowe określenia

(1.1) Definicja

Ciągiem liczbowym nieskończonym nazywamy funkcję odwzorowującą zbiór liczb naturalnych w zbiór liczb rzeczywistych f : N→R.

Wartość f(n) funkcji f dla liczby naturalnej n nazywamy n- tym wyrazem ciągu i oznaczamy np. przez a_n, zaś sam ciąg będziemy oznaczali przez a₁, a₂, a₃, ... , a_n... lub krótko (a_n).

(1.2) Definicja

Ciąg (a_n) jest ograniczony z dołu, jeżeli

(1.3) Definicja

Ciąg (a_n) jest ograniczony z góry, jeżeli

(1.4) Definicja

Ciąg (a_n) jest ograniczony, gdy

Ciąg, który nie jest ograniczony nazywamy ciągiem nieograniczonym.

(1.5) Definicja

Ciąg (a_n) jest rosnący, jeżeli

(1.6) Definicja

Ciąg (a_n) jest niemalejący, jeżeli

Uwaga. Analogicznie definiuje się ciąg malejący i nierosnący. Ciągi rosnące, malejące, nierosnące i niemalejące nazywamy monotonicznymi.

(1.7) Definicja

Ciąg (a_n) nazywamy ciągiem arytmetycznym, jeśli

Liczbę r nazywamy różnicą ciągu arytmetycznego.

(1.8) Definicja

Ciąg (a_n) nazywamy ciągiem geometrycznym, jeśli

Liczbę q nazywamy ilorazem ciągu geometrycznego.

(1.9) Twierdzenie

Jeśli (a_n) jest ciągiem arytmetycznym o wyrazie ogólnym
, to:

1. (a_n ) jest rosnący, gdy r > 0,

2. (a_n ) jest stały, gdy r = 0,

3. (a_n) jest malejący, gdy r < 0.

(1.10) Twierdzenie

Jeżeli (a_n) jest ciągiem geometrycznym o wyrazie ogólnym
, to:

1. (a_n) jest naprzemienny dla q∈R_ ,

2. (a_n) jest stały dla q=1,

3. (a_n) jest malejący dla q∈(0,1) i a₁∈R₊ lub q∈(1,∞) i a₁∈R _ ,

4. (a_n) jest rosnący dla q∈(0,1) i a₁∈R_ lub q∈(1, ∞) i a₁∈R ₊ .

(1.11) Twierdzenie

1. Jeśli (a_n) jest ciągiem arytmetycznym, to

2. Jeżeli (a_n) jest ciągiem geometrycznym, to

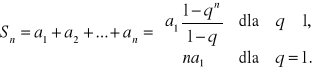
2. Granice ciągów

(2.1) Definicja

Przedział
nazywamy otoczeniem o promieniu
punktu
i oznaczamy symbolem

(2.2) Definicja

Ciąg (a_n) jest zbieżny do granicy właściwej g∈R, co zapisujemy

tzn. gdy prawie wszystkie wyrazy tego ciągu należą do otoczenia

(2.3) Twierdzenie (o jednoznaczności granicy ciągu)

Kiedy ciąg zbieżny ma dokładnie jedną granicę.

(2.4) Definicja

Ciąg (a_n) jest zbieżny do granicy niewłaściwej +∞, co zapisujemy

(2.5) Definicja

Ciąg (a_n) jest zbieżny do granicy niewłaściwej -∞, co zapisujemy

Uwaga. Ciągi, których granica właściwa ani niewłaściwa nie istnieje nazywamy

ciągami rozbieżnymi.

(2.6) Fakt

Granica ciągu zbieżnego nie zależy od wartości skończenie wielu jego wyrazów.

(2.7) Fakt (granice ciągu geometrycznego)

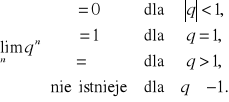
(2.8) Twierdzenie (warunek Cauchy'ego zbieżności ciągu)

Ciąg (a_n) jest zbieżny ⇔

(2.9) Definicja

Niech (a_n) będzie dowolnym ciągiem oraz niech (k_n) -rosnącym ciągiem liczb naturalnych. Podciągiem ciągu (a_n) nazywamy ciąg (b_n) określony wzorem:

(2.10) Twierdzenie ( o granicy podciągu ciągu zbieżnego)

Każdy podciąg ciągu zbieżnego jest zbieżny do tej samej granicy.

(2.11) Twierdzenie (o ograniczoności ciągu zbieżnego)

Jeżeli ciąg jest zbieżny do granicy właściwej, to jest ograniczony.

Uwaga. Implikacja odwrotna w powyższym twierdzeniu nie jest prawdziwa.

Na przykład ciąg a_n =(-1)ⁿ jest ograniczony, ale nie jest zbieżny.

(2.12) Fakt ( o równoważności granic)

(2.13) Twierdzenie ( o arytmetyce granic ciągów)

Jeżeli ciągi (a_n) i (b_n) są zbieżne do granic właściwych, to:

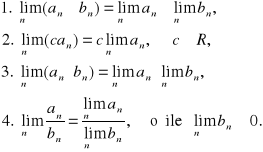
(2.14) Twierdzenie ( o trzech ciągach)

Jeżeli ciągi (a_n), (b_n) i (c_n) spełniają warunki:

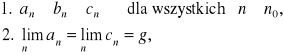
to

(2.15) Twierdzenie (o ciągu ograniczonym i zbieżnym do zera)

Jeżeli ciąg (a_n) jest ograniczony, a ciąg (b_n) jest zbieżny do 0, to

(2.16) Twierdzenie (o ciągu monotonicznym i ograniczonym)

Jeżeli ciąg (a_n) jest niemalejący dla n>n₀ oraz ograniczony z góry, to jest zbieżny dla granicy właściwej

Uwaga. Prawdziwe jest także analogiczne twierdzenie dla ciągu nierosnącego i

ograniczonego z dołu.

(2.17) Twierdzenie (określenie liczby e)

Ciąg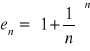
jest rosnący i ograniczony z góry, a zatem jest zbieżny.

Uwaga. Granicę tego ciągu oznaczamy przez e:

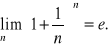
Liczba e z dokładnością do 10 cyfr po przecinku jest równa 2,7182818285.

Logarytm przy podstawie e nazywamy logarytmem naturalnym i oznaczamy przez ln;
Funkcję wykładniczą przy podstawie e nazywamy eksponens i oznaczamy przez exp;

(2.18) Fakt( o ciągach z granicą e)

Jeżeli ciąg (a_n ) o wyrazach dodatnich jest zbieżny do granicy niewłaściwej *, to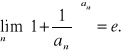

Uwaga. Fakt powyższy jest prawdziwy także wtedy, gdy ciąg (a_n ) o wyrazach ujemnych jest zbieżny do granicy niewłaściwej -*.

3. Wyrażenie nieoznaczone

Powyższe symbole nazywamy wyrażeniami nieoznaczonymi. Ich wartość zależy od postaci ciągów je tworzących.

4. Granica dolna i górna ciągów

(4.1) Twierdzenie (Bolzano -Weierstrassa)

Jeżeli ciąg jest ograniczony, to ma podciąg zbieżny do granicy właściwej.

(4.2) Definicja

1. Liczba a jest właściwym punktem skupienia ciągu, jeżeli istnieje podciąg

tego ciągu zbieżny do granicy a.

2. Symbol -∞ (∞)jest niewłaściwym punktem skupienia ciągu, jeżeli istnieje podciąg tego ciągu zbieżny do (-∞) (∞).

(4.3) Definicja

Niech S oznacza zbiór punktów skupienia ciągu (a_n) (właściwych i niewłaściwych)

1. granicę dolną ciągu (a_n) określamy wzorem

2. granicę górną ciągu (a_n) określamy wzorem

Ważne wzory:

1

5

---