GRANICA FUNKCJI

1. Definicje granic

(1.1) Definicja

Sąsiedztwem o promieniu
punktu x₀ nazywamy zbiór

Porównując tę definicję z definicją otoczenia punktu x₀ stwierdzamy, że

Niech funkcja f będzie określona w pewnym sąsiedztwie S punktu x₀.

(1.2) Definicja (Heinego) (ciągowa)

Liczbę g nazywamy granicą funkcji f w punkcie x₀ , jeżeli dla każdego ciągu (x_n) o wyrazach
zbieżnego do x₀, ciąg
jest zbieżny do g.

Symboliczny zapis:

(1.3) Definicja (Cauchy'ego)(otoczeniowa)

(1.4) Fakt

Definicje Heinego i Cauchy'ego granicy funkcji w punkcie są równoważne.

Przykłady granic:

1)
2)
.

3)
. 4)
.

5)
. 6)
.

2. Własności granic

(2.1) Twierdzenie (o działaniach arytmetycznych na granicach funkcji)

Jeżeli
i
to

1)

2)
,

3)
przy p ≠ 0,

4)
c- stała,

6)
.

(2.2) Twierdzenie (o granicy funkcji złożonej)

Jeżeli:

1)

2)

3)

to
.

Przykład:

.

3. Granice niewłaściwe, jednostronne, w -∞ albo +∞.

Niech funkcja f będzie określona w pewnym sąsiedztwie S punktu x₀.

(3.1) Definicja (Heinego)

1. Funkcja f ma w punkcie x₀ granicę niewłaściwą -∞, co zapisujemy
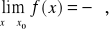
   jeżeli dla każdego ciągu (x_n) o wyrazach x_n * S, zbieżnego do x₀, ciąg (f(x_n)) jest zbieżny do -∞.

2. Funkcja f ma w punkcie x₀ granicę niewłaściwą +∞, co zapisujemy
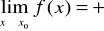
   , jeżeli dla każdego ciągu (x_n) o wyrazach x_n * S, zbieżnego do x₀, ciąg (f(x_n)) jest zbieżny do +∞.

(3.2) Definicja (Cauchy'ego)

1. 
   

2. 
   

Uwaga. Jeżeli w określeniu granicy funkcji f w punkcie x₀ właściwej albo niewłaściwej, zastąpić sąsiedztwo S punktu x₀ sąsiedztwem lewostronnym (albo prawostronnym) tego punktu, to otrzymamy definicję granicy lewostronnej funkcji f w punkcie x₀ (odpowiednio prawostronnej).

Granice te nazywamy granicami jednostronnymi i oznaczamy następująco:

,
.

Przykładowe definicje jednostronne Cauchy'ego mają postać:

.

Przykłady:
,
,
,
,

(3.3) Twierdzenie (warunek konieczny i wystarczający istnienia granicy funkcji)

.

Niech funkcja f będzie określona w przedziale (-∞, a).

(3.4) Definicja (Heinego)

1. Funkcja f ma w -∞ granicę g, co zapisujemy
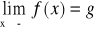
   , jeżeli dla każdego ciagu (x_n) o wyrazach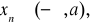
   zbieżnego do -∞, ciąg (f(x_n)) jest zbieżny do g.

2. Funkcja f ma w -∞ granicę niewłaściwą -∞(∞), co zapisujemy
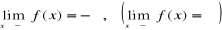
   , jeżeli dla każdego ciagu (x_n) o wyrazach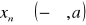
   , zbieżnego do -∞, ciąg (f(x_n))jest zbieżny do -∞(∞).

(3.5) Definicja (Cauchy'ego)

1)

2)

3)
.

Podobnie określamy granicę
i granice niewłaściwe
.

Niektóre granice funkcji:

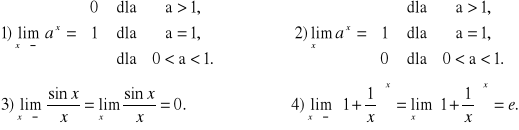
Uwaga. Dla granic jednostronnych pozostaje w mocy twierdzenie o działaniach arytmetycznych na granicach funkcji i o granicy funkcji złożonej, przy czym należy ostrożnie korzystać z tych twierdzeń w przypadku granic niewłaściwych.

(3.6) Twierdzenie (o trzech funkcjach)

Jeżeli f, g, h spełniają warunki:

1.
dla każdego

2.
, to
.

(3.7) Twierdzenie (o dwóch funkcjach)

Jeżeli funkcje f, g spełniają warunki:

1.
dla każdego
,

2.
, to
.

CIĄGŁOŚĆ FUNKCJI

1. Ciągłość funkcji

(1.1) Definicja

Otoczeniem lewostronnym o promieniu
punktu
nazywamy zbiór

Otoczeniem prawostronnym o promieniu
punktu
nazywamy zbiór

(1.2) Definicja

Niech
oraz niech funkcja f będzie określona przynajmniej na

Funkcja f jest ciągła w punkcie

(1.3) Definicja (Heinego)

Funkcja f jest ciągła w punkcie

(1.4) Definicja (Cauchy'ego)

Funkcja f jest ciągła w punkcie

(1.5) Definicja

Niech
oraz niech funkcja f będzie określona przynajmniej na

Funkcja f jest lewostronnie ciągła w punkcie

Uwaga. Analogicznie definiuje się funkcję prawostronnie ciągłą.

(1.6) Twierdzenie (warunek konieczny i wystarczający ciągłości funkcji)

Funkcja f jest ciągła w punkcie * jest w tym punkcie ciągła lewostronnie i prawostronnie.

(1.7) Definicja

Funkcja jest ciągła w przedziale otwartym
, jeżeli jest ciągła w każdym punkcie tego przedziału.

Funkcja jest ciągła w przedziale domkniętym
, jeżeli jest ciągła w
oraz prawostronnie ciągła w punkcie a i lewostronnie ciągła w punkcie b.

Analogicznie definiujemy ciągłość funkcji na przedziałach

2. Nieciągłości funkcji

(2.1) Definicja

Niech
oraz niech funkcja f będzie określona przynajmniej na

Funkcja f jest nieciągła w punkcie
nie istnieje granica

albo, gdy

Uwaga. Nieciągłość funkcji można rozważać jedynie w punktach należących do jej dziedziny.

(2.2) Definicja

Funkcja f ma w punkcie
nieciągłość pierwszego rodzaju, jeżeli istnieją granice skończone

takie, że
lub
, przy czym

1. jeśli
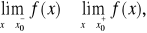
   to jest to nieciągłość typu „skok”,

2. jeśli
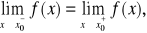
   to jest to nieciągłość typu „luka”.

(2.3) Definicja

Funkcja f ma w punkcie
nieciągłość drugiego rodzaju, jeżeli co najmniej jedna z granic

nie istnieje lub jest niewłaściwa.

3. Działania na funkcjach ciągłych

(3.1) Twierdzenie(o ciągłości sumy, różnicy, iloczynu, ilorazu funkcji ciągłych)

Jeżeli funkcje f i g są ciągłe w punkcie
, to w tym punkcie ciągłe są również funkcje f + g, f - g, k f, f g, a także f / g, gdy

(3.2) Twierdzenie ( o ciągłości funkcji złożonej)

Jeżeli funkcja f jest ciągła w punkcie
, funkcja g jest ciągła w punkcie
i istnieje superpozycja
, to funkcja złożona
jest ciągła w punkcie
.

(3.3) Twierdzenie ( o ciągłości funkcji odwrotnej)

Niech I oraz J będą dowolnymi przedziałami.

Jeżeli funkcja
jest ściśle monotoniczna i ciągła, to funkcja odwrotna
także jest ciągła.

(3.4) Twierdzenie ( o ciągłości funkcji elementarnych)

Funkcje elementarne są ciągłe w swoich dziedzinach.

(3.5) Twierdzenie(Weierstrassa o ograniczoności funkcji ciągłej)

Jeżeli funkcja f jest ciągła w przedziale domkniętym, to jest w nim ograniczona.

Uwaga. Założenie domkniętości przedziału jest istotne, gdyż np. funkcja
jest ciągła na przedziale
, ale nie jest na nim ograniczona.

Podobnie założenie ciągłości funkcji jest istotne, gdyż np. funkcja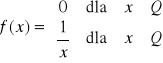
nie jest ograniczona na przedziale domkniętym

(3.6) Twierdzenie (Weierstrassa o osiąganiu kresów)

Jeżeli funkcja f jest ciągła w przedziale domkniętym
, to

(3.7) Twierdzenie( Darboux o przyjmowaniu wszystkich wartości pośrednich)

Jeżeli funkcja f jest ciągła w przedziale domkniętym
oraz spełnia warunek
, to

(Każda prosta
, gdzie
przecina wykres funkcji f co najmniej raz).

(3.8) Twierdzenie(Darboux o miejscach zerowych funkcji)

Jeżeli funkcja f jest ciągła w przedziale domkniętym
oraz spełnia warunek
to istnieje punkt
taki, że

3. Jednostajna ciągłość funkcji

(4.1) Definicja(Cauchy'ego)

Niech I oznacza dowolny przedział. Funkcja f jest jednostajnie ciągła na przedziale I *

Uwaga. Każda funkcja jednostajnie ciągła w przedziale, jest w tym przedziale

ciągła.

Twierdzenie odwrotne nie jest prawdziwe. Kontrprzykład: Funkcja
jest ciągła w
, ale nie jest w nim jednostajnie ciągła.

(4.2) Twierdzenie (Cantora-warunek wystarczający jednostajnej ciągłości)

Funkcja ciągła w przedziale
jest w nim jednostajnie ciągła.

1

6

---