Model Michaelisa-Menten

W ćwiczeniu zadano wartości C_s (stężenie substratu) oraz r (szybkość reakcji). Sporządzono wykres:

Następnie sporządzono wykres odwrotności Lineweavera-Burke'a. Zastosowano linearyzację punktów, co pozwoliło na wyznaczenie szybkości maksymalnej V_max i stałej Michaelisa K_M.

Równanie wyznaczonej prostej:

y = 4x + 6,6667

(y = ax + b)

Stąd możliwe było policzenie parametrów kinetycznych reakcji:

Następnym etapem była weryfikacja wyników w reaktorze okresowym. W tym celu obliczono dokładne stężenie substratu wg. wzoru:

Początkowe stężenie substratu wynosiło 30. Na podstawie tak wyliczonych danych wyznaczono czas modelowy reakcji w celu zestawienia go z czasem rzeczywistym.

np.:

Krzywa dla czasu modelowego idealnie pokrywa się z krzywą dla rzeczywistego czasu reakcji. Oznacza to poprawność wyznaczonych danych.

Model Michaelisa-Menten z inhibicją substratową

W ćwiczeniu zadano wartości C_s (stężenie substratu) oraz r (szybkość reakcji), podobnie jak w poprzednim przypadku. Sporządzono wykres:

Następnie sporządzono wykres odwrotności Lineweavera-Burke'a. Zastosowano linearyzację punktów, co pozwoliło na wyznaczenie szybkości maksymalnej V_max i stałej Michaelisa K_M.

Na jego podstawie stwierdzono możliwość występowania inhibicji substratowej, czyli przypadku, gdy substrat użyty w wyższych stężeniach hamuje aktywność enzymu. Konieczne okazało się wyznaczenie stałej inhibicji K_is jako kolejnego parametru. W tym celu użyto programu Origin Pro 8 i za jego pomocą skorzystano z funkcji regresji nieliniowej (Nonlinear curie fit).

Otrzymane wyniki:

V_max = 0,15 ± 1,227·10^-16

K_m = 0,60 ± 1,595 · 10^-15

K_is = 50 ± 1,557 · 10^-13

Podobnie jak w poprzednim schemacie, początkowe stężenie substratu wynosiło 30. Na podstawie wyżej wyliczonych danych wyznaczono czas modelowy reakcji, uwzględniając stałą inhibicji K_is. Jest to postać całkowa równania Michaelisa-Menten:

np.:

Model Michaelisa-Menten dla izoenzymów

Izoenzymy są to enzymy różniące się sekwencją, katalizujące tą samą reakcję chemiczną. Z reguły wykazują inne właściwości katalityczne jak na przykład K_m czy V_max. Są wykrywalne metodą elektroforetyczną, nie powodują widocznych zmian fenotypu, ponieważ pełnią tą samą funkcję w organizmie. Gdy przeprowadzamy doświadczenie wykorzystujące dwa izoenzymy i mamy na celu zbadanie ich właściwości katalitycznych, należy postępować następująco:

1. Sporządzić wykres zależności r/C_s od r, gdzie r jest szybkością reakcji a C_s stężeniem substratu, powinno to wyglądać w ten sposób

2. Następnym krokiem jest linearyzacja ostatnich paru punktów (ok. 5) oraz poprowadzenie linii trendu wraz z jej równaniem, wygląda to następująco:

3. Korzystamy z równania prostej by wyznaczyć parametry katalityczne pierwszego z izoenzymów reakcji V_max1 i K_m1. Punkt przecięcia linii trendu z osią X, czyli podstawienie Y=0 do równania pozwoli nam wyznaczyć V_max1, natomiast podstawienie X=0 wyznacza punkt przyjmujący wartość V_max1/K_m1. Obliczając wcześniej wartość prędkości maksymalnej można z łatwością wyznaczyć stałą Michaelisa. Mając te oba parametry dla pierwszego enzymu należy przystąpić do obliczenia ich dla drugiego, w tym celu korzystamy z równania Michaelisa-Menten aby obliczyć r₂, ponownie wyznaczamy wartość r₂/C_s i rysujemy kolejny wykres zależności r₂/C_s od r₂. Postępujemy identycznie jak w pierwszym przypadku. Mając wartości obliczone na podstawie wykresu należy użyć programu Origin Pro 8, który za pomocą regresji nieliniowej wykresu r od C_s policzy nam dokładnie owe parametry. Przykładowe obliczenia:

r - całkowita szybkość reakcji

r₁ - szybkość przeprowadzania reakcji dla pierwszego izoenzymu

r₂ - szybkość przeprowadzania reakcji dla drugiego izoenzymu

Równanie prostej

y = -1,6811x + 0,8391

V_max1, Y = 0

0 = -1,6811x+0,8391

1,6811x = 0,8391

x = 0,8391/1,6811 = 0,5 [M/min]

K_m1, X = 0

V_max1/K_m1 = 0,8391

K_m1 = V_max/0,8391 = 0,59 [M]

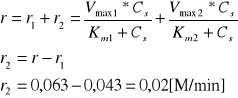
Parametry obliczone przez Origin Pro 8:

	Value	Standard Error
Vmax1	0,2	9,86E-16
Km1	1,5	1,29E-14
Vmax2	0,3	1,04E-15
Km2	0,1	5,74E-16

Ostatecznie stwierdzamy, że szybkość reakcji jest wypadkową szybkości obu enzymów, co ilustruje poniższy wykres.

Reakcje inhibicji produktem

Zwane też inhibicją poprzez sprzężenie zwrotne. Ten typ regulacji aktywności enzymatycznej polega na hamowaniu wcześniejszych reakcji przez powstały produkt. Jest to bardzo często występujący mechanizm w szlakach metabolicznych, gdzie produkt końcowy przyłącza się do miejsca allosterycznego pierwszego enzymu szlaku powodując jego dezaktywację, co pozbawia substratów wszystkie pozostałe enzymy szlaku.

W tym wypadku chcąc zbadać parametry kinetyczne enzymu należy wykonać następujące kroki:

1. Wykonać wykres stężenia produktu (C_p) od czasu reakcji (t). Należy potem skorzystać z zależności C_s = C_s0 - C_p, aby obliczyć stężenie rzeczywiste substratu.

2. Mając stężenia rzeczywiste substratu C_s oraz szybkość reakcji r należy sporządzić wykres, dla sprawdzenia słuszności obranej metody:

3. Następnym krokiem jest obliczenie odwrotności 1/C_s i 1/r, w celu wykonania wykresu Lineweaver'a - Burka, zależność 1/r od 1/Cs, trzeba poprowadzić linię trendu i przy pomocy jej równania wyznaczyć V_max i K_m enzymu. Odwrotność wyrazu wolnego z równania da nam wartość V_max, natomiast współczynnik kierunkowy prostej podzielony przez wyraz wolny to K_m. Po obliczeniu wartości te również sprawdzamy w programie Origin Pro 8 z użyciem odpowiedniej formuły.

Przykładowe obliczenia:

Równanie prostej

y = 4x + 6,6667

V_max = 1/6,6667 = 0,15 [M/min]

K_m = 4/6,6667 = 0,60 [M]

Parametry obliczone z Origin Pro 8:

V_max = 0,16846

K_m = 2

K_i = 10

Odchylenie standardowe do powyższych wartości było bardzo duże, komputer nic nie pokazał.

4. Słuszność naszych założeń należy zweryfikować w reaktorze okresowym, wykonując pomiary stężenia produktu w określonych odstępach czasu. Aby następnie obliczyć stężenie substratu w danej chwili należy skorzystać z zależności C_s = C_s0 - Cp, gdy uzyskamy wartości stężenia rzeczywistego substratu C_s, czasu rzeczywistego reakcji t, stałej Michealisa oraz prędkości maksymalnej, możemy przystąpić do obliczenia czasu modelowego reakcji, korzystając z całkowej postaci równania Michaelisa-Menten. Na podstawie wartości czasu modelowego reakcji jesteśmy w stanie zweryfikować swoje poprzednie założenie. Na koniec należy wykonać wykres czasu od stężenia substratu, nanosząc na niego czas modelowy i rzeczywisty. Jeżeli ćwiczenie zostało wykonane poprawnie, wykres powinien wyglądać następująco:

Czas modelowy odbiega od rzeczywistego, mamy do czynienia z innym przypadkiem inhibicji. Wraz ze wzrostem stężenia produktu czas reakcji znacznie się wydłuża, co wskazuje na to, iż produkt jest jednocześnie inhibitorem reakcji.

Za pomocą programu Origin Pro 8 wyznaczono parametry kinetyczne reakcji:

Vmax, Km oraz Kip.

Otrzymano następujące wyniki:

Vmax = 0,15 ± 523,844 [M/min]

Km = 0,5 ± 106203,466 [M]

K_ip = 0,4 ± 177799,602 [M]

Czas modelowy reakcji jest zbliżony do czasu zmierzonego w reaktorze okresowym (mimo odchylenia standardowego rzędu 10⁶).

Przykładowe obliczenia:

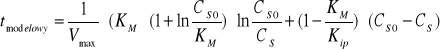
[min]

Źródła:

- http://en.wikipedia.org/wiki/Isozyme

- E.P. Solomon, L.R. Berg, D.W. Martin, C.A. Ville. Biologia - wydanie pierwsze (według III wydania amerykańskiego), MULTICO Oficyna Wydawnicza, Warszawa 1996

Sprawozdanie 2. Strona 1 z 11	Politechnika Wrocławska Wydział Chemiczny	Dr hab. Jolanta Bryjak, prof. PWr Śr, godz. 17-21, bud.C6/125
Laboratorium Inżynieria Bioreaktorów	Kinetyka enzymatyczna - komputery	Wojciech Ślęczek 168560 Maciej Duda 168516

---