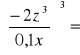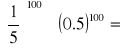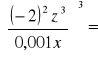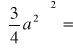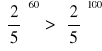Arkusz hospitacji diagnozującej
Imię i nazwisko nauczyciela |
|
Przedmiot - rodzaj zajęć |
matematyka |
Klasa - grupa |
II |
Temat lekcji - zajęć |
Potęga o wykładniku całkowitym i notacja wykładnicza - zabawy matematyczne |
Data hospitacji |
|
Cel ogólny |
Obserwacja osiągniętego poziomu sprawności uczniowskich i umiejętności. |
Cele szczegółowe: |
Diagnoza następujących umiejętności kluczowych: efektywnego współdziałania w zespole i pracy w grupie, podejmowania indywidualnych i grupowych decyzji, rozwiązywania problemów w sposób twórczy, poszukiwania, wykorzystywania informacji z różnych źródeł |
Imię i nazwisko hospitującego |
|
Strategiczne umiejętności ucznia opisane w podstawie programowej kształcenia ogólnego |
Adnotacja hospitowanego |
Adnotacja hospitującego |
|
|
Stopień opanowania |
Stopień opanowania |
|
Efektywnego współdziałania w zespole |
4 |
|
|
Dzielenie się zadaniami |
3 |
|
|
Dzielenie się wiedzą, pomysłami |
3 |
|
|
Podejmowanie decyzji |
grupowe |
4 |
|
|
indywidualne |
2 |
|
Przestrzeganie zasad uczciwej rywalizacji |
5 |
|
|
Wykorzystywania informacji z różnych źródeł |
3 |
|
|
Stopień opanowania materiału w zakresie koniecznym i podstawowym |
4 |
|
|
Rozwiązywania problemów w sposób twórczy |
2 |
|
|
Inne uwagi i spostrzeżenia hospitowanego |
Zadowolona byłam, że uczniowie słabi, którym matematyka sprawia problemy, nieśmiali oraz bierni na lekcjach tym razem wykazali duże zainteresowanie oraz chęć podejmowania wysiłku intelektualnego. Chętnie wykonywali powierzone im zadania, sami z własnej inicjatywy próbowali rozwiązywać problemy, współpracowali z kolegami. |
Inne uwagi i spostrzeżenia hospitującego |
|
Wspólne wnioski i indywidualne zalecenia |
Zachęcać najsłabszych, bądź nieśmiałych uczniów do wysiłku intelektualnego oraz większej aktywności na lekcjach matematyki poprzez większą ilość gier dydaktycznych oraz stosowanie metod aktywizujących. Motywować uczniów do częstszego podejmowania indywidualnych decyzji. Pracować nad umiejętnością rozwiązywania problemów w sposób twórczy. |
Data rozmowy po hospitacyjnej |
|
Podpis hospitowanego |
Podpis hospitującego |
Stopień opanowania umiejętności ucznia według skali ocen.
Data:
Konspekt lekcji matematyki w klasie II E
Lekcja przeznaczona na 2 godziny lekcyjne.
Temat lekcji: Potęga o wykładniku całkowitym i notacja wykładnicza - zabawy matematyczne
Cel ogólny: obserwacja osiągniętego poziomu sprawności uczniowskich i umiejętności.
Cele szczegółowe - Diagnoza następujących umiejętności kluczowych:
efektywnego współdziałania w zespole i pracy w grupie, podejmowania indywidualnych i grupowych decyzji, rozwiązywania problemów w sposób twórczy, poszukiwania, wykorzystywania informacji z różnych źródeł
Organizacja pracy:
praca w pięcioosobowych grupach
Metody:
Metoda warsztatowa
Środki dydaktyczne:
Trzy gry matematyczne, kalkulator, zeszyt z notatkami lekcyjnymi, podręczniki do matematyki, instrukcje do gier sporządzone przez nauczyciela.
Omówienie lekcji.
Lekcja kończy się dziesięciominutowym omówieniem. Nauczyciel zadaje graczom pytania tak, aby zrozumieć dlaczego pewne pytania nie sprawiły trudności , inne natomiast sprawiły.
Zasady gry pierwszej - Układanka
Uczniowie dostają karteczki z częściowymi informacjami, które muszą dobierać w pary, tak aby obydwie informacje stanowiły logiczną całość.
Za każdą poprawnie wskazaną parę dostają 1 punkt.
Dozwolone posługiwanie się kalkulatorem, zeszytem podręcznikiem.
Czas pracy 25 minut.
Zasady gry drugiej -Tabelka.
Uczniowie dostają tabelkę częściowo wypełnioną przez nauczyciela. Resztę tabelki mają wypełnić samodzielnie.
Nie .dozwolone posługiwanie się kalkulatorem, zeszytem podręcznikiem. Należy wykorzystać jedynie informację pomocnicze zawarte w tabeli.
Za każdą poprawnie wypełniona komórkę tabeli dostają 1 punkt.
Czas pracy 10 minut.
X |
X2 |
X3 |
Y |
Y2 |
Y3 |
0,07 |
|
|
7 |
49 |
343 |
0,12 |
|
|
12 |
144 |
1728 |
23000 |
|
|
23 |
529 |
12167 |
90 |
|
|
9 |
81 |
729 |
Zasady gry trzeciej - Turniej Matematyczny
Klasę dzielimy na 4 do 5 grup pięcioosobowych.
Grupa losuje numer pytania, a pytanie zostaje odczytane na głos, lub wyświetlone na rzutniku.
Grupa ma czas 5 minut na zastanowienie się nad odpowiedzią. Odpowiada jedna osoba z grupy.
Jeśli odpowiedź jest prawidłowa grupa otrzymuje punkt i wybiera grupę losującą pytanie. Dwa razy w czasie turnieju może wybrać samą siebie. Jeśli nie uda się jej odpowiedzieć prawidłowo na pytanie losujemy grupę, która otrzyma szansę na odpowiedź. Jeśli odpowie poprawnie obowiązują ja te same zasady, jeśli nie losujemy kolejną odpowiadającą grupę.
Ważne jest żeby za każdym razem odpowiedzi na wylosowane pytanie udzielała inna osoba, natomiast dozwolone jest, aby nad odpowiedzią pracował cały zespół. Można posługiwać się kalkulatorem, zeszytem podręcznikiem.
Wygrywa grupa, która zdobyła najwięcej punktów.
Czas pracy 35 minut, 5 minut na zapoznanie z regulaminem gry oraz podsumowanie wyników.
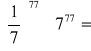
PONIŻEJ KARTA DO GRY PIERWSZEJ - UKŁADANKIA
|
|
|
|
Nierówność prawdziwa |
Równanie prawdziwe |
|
0,343 |
|
|
Nierówność prawdziwa |
Równanie prawdziwe |
|
0,0343 |
|
|
Nierówność prawdziwa |
Równanie nieprawdziwe |
|
1 |
|
|
Nierówność prawdziwa |
Równanie nieprawdziwe |
|
1,21 |
|
|
Nierówność nieprawdziwa |
|
|
0,0121 |
|
|
Nierówność nieprawdziwa |
|
|
|
|
|
Nierówność nieprawdziwa |
|
|
|
|
|
Nierówność nieprawdziwa |
|
|
|
|
|
Nierówność nieprawdziwa |
|
Gra „Turniej Matematyczny” może być wykorzystana także w organizacji konkursów szkolnych, zatem zamieszczamy przykłady innych zadań (niektóre o podwyższonym stopniu trudności).
1. Agnieszka, Dorota, Ewa i Kasia mają razem 1570 znaczków. Gdyby Agnieszka dokupiła
30 znaczków, a Kasia podarowała Dorocie 10, a Ewie 20 znaczków, to każda z dziewcząt
będzie miała po tyle samo znaczków.
Agnieszka ma 370 znaczków;
Ewa i Kasia mają razem 700 znaczków;
Dorota ma 330 znaczków.
2. Na bieżni stadionu długości 0,4 km odbył się rajd pomiędzy Arturem, który jechał na
motorze, i Agatą, która jechała na motorynce. Oboje wystartowali jednocześnie z jednego
punktu bieżni i jechali w przeciwnych kierunkach. Artur poruszał się ze średnią prędkością 70
km/h, a Agata 25 km/h. W momencie, kiedy Agata przejechała 50 okrążeń, zatrzymał się
również Artur.
Agata przejechała 25 km;
Artur przejechał 56 km;
Zatrzymali się w punkcie, w którym wystartowali.
3. W trójkącie ABC AC=![]()
BC=5, wysokość CD opuszczona na bok AB równa jest 4.
długość trzeciego boku wynosi 9;
pole wynosi 36;
wysokość opuszczona na bok CB wynosi 7,2
4. Basen ma kształt prostopadłościanu, którego długość jest równa 20 m, a szerokość 12 m. Objętość wody jest równa 312m3.
wysokość wody wlanej do basenu wynosi 1,3 m;
po dolaniu 48 m3 poziom wody podniesie się o 0,1 m;
pole podstawy ostrosłupa, którego objętość i wysokość są równe objętości i wysokości wody w basenie (przed dolaniem) wynosi 720 m2.
5. W pewnej szkole podstawowej 65% uczniów uczy się języka angielskiego, a 78% uczy
się języka niemieckiego. Każdy uczeń uczy się co najmniej jednego języka. Obu języków
uczy się 172 uczniów.
W szkole tej jest 400 uczniów;
13% uczniów uczy się obu języków;
tylko angielskiego uczy się 80 uczniów.
f
6. Graniastosłup prosty o krawędziach podstawy równych 3 i 4 oraz wysokości równej 12,
przecięto płaszczyzną przechodzącą przez przekątne obu podstaw.
objętość graniastosłupa wynosi 144:
pole powierzchni całkowitej wynosi 216;
pole przekroju stanowi 31,25% pole powierzchni całkowitej.
7. W ostrosłupie prawidłowym sześciokątnym, krótsza przekątna podstawy jest równa 6V3
cm ,a wysokość ściany bocznej jest równa 12 cm:
pole powierzchni bocznej wynosi 216 cm2
pole powierzchni podstawy wynosi 54
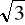
cm2pole powierzchni całkowitej (216 + 108
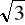
) cm2
8. Oblicz wartość wyrażenia: 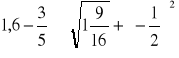
9 Wyrażenie ![]()
sprowadź do najprostszej postaci i oblicz jego wartość liczbową dla ![]()
10 Pojemnik w kształcie prostopadłościanu o wymiarach 3 cm, 0,4 dm, 5 cm napełniono w 2/5 piaskiem. Ile dm3 piasku znajduje się w pojemniku ?
Narysuj wykres funkcji
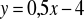
Oblicz dla jakiego argumentu funkcja ta przyjmuje wartość -5.Wskazówka minutowa zegara ściennego ma 9 cm długości. Jaką długość przebędzie koniec tej wskazówki w ciągu 20 min ?
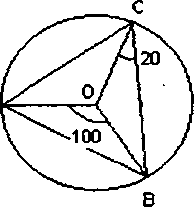
Trójkąt wpisano w okrąg o środku O, tak jak na rysunku. Znajdź miarę kąta AOC.
14 Znajdź najmniejszą liczbę całkowitą spełniającą nierówność ![]()
Zadanie 15 Sto złotych monet spakowano w rolki po dziesięć monet w każdej. W jednej rolce monety są nieprawdziwe i każda z nich waży 9g, w pozostałych prawdziwe ważące po l0g. Jak za pomocą wagi i jednego warzenia sprawdzić która rolka zawiera fałszywe monety. Uwaga: Masz do dyspozycji wagę szalkową lub elektroniczną.
Zadanie 16 Oblicz iloczyn ![]()
Zadanie 17 Czy liczba ![]()
może być kwadratem liczby naturalnej?
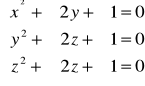
Zadanie 18 Rozwiąż układ równań:
Zadanie 19 Sześciokąt foremny ma pole równe 36. Oblicz pole gwiazdy sześcioramiennej wyznaczonej przez krótsze przekątne tego sześciokąta. Wskazówka: Pole trójkąta równobocznego o bokach równych a jest równe
![]()
zaś suma kątów w sześciokącie wynosi 720°.
GRY LOGICZNE
BRACIA MARX PRACUJĄ Bracia Marx podjęli nową pracę jako przewoźnicy mebli i właśnie ładują stoły do meblowozu. Gdyby Groucho pracował sam, zapełniłby pusty meblowóz w ciągu 12 minut. Harpo zrobiłby to w ciągu 13,5 minuty. Natomiast trzeciemu z braci — Chico — opróżnienie załadowanego meblowozu zajmuje 14 minut. Jak można się domyślić, Groucho i Harpo ładują stoły, podczas gdy Chico wynosi je z meblowozu. Oblicz, jak długo Groucho i Harpo muszą pracować, pamiętając o tym, iż Chico przez cały czas rozładowuje samochód.
|
ZEGARY Mała Sue, siostrzyczka londyńskiego „Big Bena", o północy wskazywała dobry czas, ale śpieszy się 51 minut na godzinę. Widzisz, że wskazuje teraz 9.15 i wiesz, że zatrzymała się dokładnie 2 godziny temu. Jaka jest teraz prawdziwa godzina?
|
|
OD WINY DO KARY A oto rzeczywiście trudna łamigłówka. Mu^ sisz przekształcić słowo WINA w słowo KARA w możliwie najmniejszej liczbie ruchów, zmieniając każdorazowo po jednej literze. Po każdej zmianie musi powstać prawidłowe polskie słowo.
|
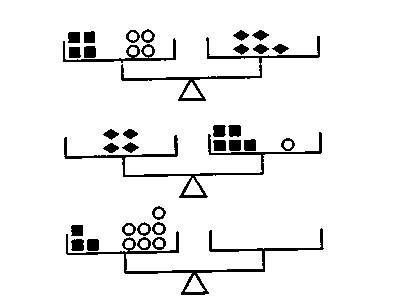
WAŻENIE Czy potrafisz powiedzieć, ilu figur brakuje na prawej szalce dolnej wagi?
|
NIEMOŻLIWE PUDEŁKA Cztery spośród pokazanych pudełek powstał po złożeniu narysowanej obok siatki, dwa zaś nie. Które?
|
OKREŚL DOKŁADNY CZAS O której godzinie — dokładnie — między godziną trzecią a czwartą, minutowa wskazówka zegarka znajdzie się idealnie na wskazówce godzinowej? |
Wstaw brakujące symbole działań arytmetycznych [(5 ? 9) ? 4] ? 8 = 19,25 |
1 Lecący gąsior spotkał na swej drodze lecący w przeciwną stronę klucz gęsi.
Witajcie, sto gęsi! - przywitał je.
Nie ma nas sto - odparła pierwsza gęś. - Jednak gdyby było nas jeszcze raz tyle, i jeszcze połowa, i jeszcze ćwierć naszego klucza i jeszcze ty razem z nami, to wtedy byłoby nas sto. Ile gęsi liczy ten klucz?
2 Do Domu Turysty w Zakopanem przybyło wieczorem trzech turystów. Zamówili na rano jedną dużą porcję pierogów. Gdy słońce wzeszło, pierwszy turysta, obudzony wyśmienitym zapachem pierogów ruskich wstał i zjadł 1/3, po czym położył się spać. Zaraz potem wstał drugi i, nie wiedząc, że pierwszy wstał przed nim, zjadł 1/3 pozostałych. Po czym też położył się spać. Trzeci turysta, kiedy się obudził, również zjadł 1/3 pierogów, które były na talerzu. On również położył się z powrotem. Kiedy wstali o 9 rano, stwierdzili, że zostało 8 pierogów. Jak podzieliłbyś pozostałe pierogi, aby każdy z nich zjadł tyle samo pierogów tegoż słonecznego poranka? Ile pierogów przyniósł kelner?
3 W okrąg wpisano regularną, pięcioramienną gwiazdę. Jaką miarę ma kąt a???
4 Przy okrągłym stole siedzi pięć osób: prawdomówcy i kłamcy. Każdy z nich wypowiada zdanie „Obaj moi sąsiedzi to kłamcy". Zakładając, że prawdomówca zawsze mówi prawdę, a kłamca zawsze kłamie, jakie jest możliwe
ustawienie tych osób przy stole.
5 Podziel wzdłuż linii daną figurę na trzy jednakowe części:
6 W pewne listopadowe popołudnie, kiedy obiad już dawno strawiłem, mama poleciła mi usmażyć trzy kotlety schabowe. Wszystko było już naszykowane, przyprawione - musiałem jedynie dokończyć dzieło. Był tylko jeden problem - na patelni mieściły się jedynie dwa kotlety, każdy z nich należało smażyć minutę z każdej strony, a gazu starczyło jedynie na trzy minuty. Nie mając do dyspozycji dodatkowych zapasów propanu-butanu ani dodatkowych naczyń, udało mi się usmażyć te kotlety. W jaki sposób?
7 Dwaj ojcowie i dwaj synowie zjedli razem trzy jabłka, każdy po całym jabłku. Czy to możliwe?
8 Firma „Diament sp. z o.o." trudni się handlem tym drogocennym kruszcem. Diamenty kupuje w Afryce i przywozi je do Europy. Tu sprzedaje je dwukrotnie drożej niż sama za nie zapłaciła. Po ich sprzedaży opłaca koszty transportu, ubezpieczenia, itd., itp., w wysokości 1500 USD, po czym ponownie kupuje diamenty na czarnym kontynencie. Po czterech takich kursach okazało się, że na koncie firmy nie ma już pieniędzy.
Ile wynosił kapitał początkowy firmy?
Ile powinien wynosić, aby działalność firmy była rentowna (aby firma przynosiła zyski)?
9. Koło, trójkąt równoboczny, kwadrat i sześciokąt foremny mają ten sam obwód
równy a. Uporządkuj figury według ich pola powierzchni - od najmniejszego do
największego. Oblicz pole każdej z nich.
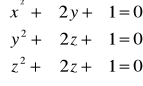
![]()
Wyszukiwarka
Podobne podstrony:
HOSPITACJA (2), wf konspekty
Nauka podań i chwytów piłki koszykowej sprzed klatki piersiowej, wf konspekty
po, konspekty AWF,WF, konspekty, Gimnastyka korekcyjna, Gimnastyka korekcyjna
nauka skoku kucznego przez skrzynię, konspekty AWF,WF, konspekty, Gimnastyka korekcyjna, GIMNASTYKA
Konsekwencje nie leczonych wad postawy, konspekty AWF,WF, konspekty, Gimnastyka korekcyjna, Gimnast
nauka zabaw, konspekty AWF,WF, konspekty, konspekty, konspekty
osnowa - ćwiczenia a rozciągnięcie mięśni barkowych, konspekty AWF,WF, konspekty, konspekty, konspe
PODZIAŁ ĆWICZEŃ GIMNASTYCZNYCH, wf konspekty
sprawność ogólna - 6ta chłopcy, konspekty AWF,WF, konspekty, Gimnastyka korekcyjna, GIMNASTYKA
przewrotu w przód 4 dziewczynki, konspekty AWF,WF, konspekty, Gimnastyka korekcyjna, GIMNASTYKA
Plecy płaskie, konspekty AWF,WF, konspekty, Gimnastyka korekcyjna, Gimnastyka korekcyjna2
Kl. lejkowata, konspekty AWF,WF, konspekty, Gimnastyka korekcyjna, Gimnastyka korekcyjna
Olimpiada klas trzecich - fajny konspekt, konspekty AWF,WF, konspekty, konspekty, konspekty
gimnastyka(przerzut bokiem), konspekty AWF,WF, konspekty, GIMNASTYKA
Plecy okrągłe3, konspekty AWF,WF, konspekty, Gimnastyka korekcyjna, Gimnastyka korekcyjna2
więcej podobnych podstron