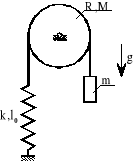
1. Napisać równania Hamiltona dla wahadła fizycznego z ruchomym punktem zawieszenia A, przy czym yA = A cost. Ruch wahadła jest ograniczony do płaszczyzny xy.
A, stałe
3. OD RÓWNAŃ KANONICZNYCH HAMILTONA DO STEROWANIA
3.1 Równania kanoniczne Hamiltona
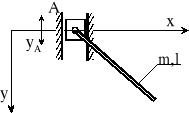
1. Napisać równania Hamiltona dla wahadła fizycznego z ruchomym punktem zawieszenia A, przy czym yA = A cost. Ruch wahadła jest ograniczony do płaszczyzny xy.
A, stałe

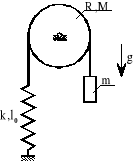
2. Dla układu przedstawionego na rysunku wyprowadzić równania kanoniczne Hamiltona.
3. Energia kinetyczna T i energia potencjalna V punktu materialnego poruszającego się w
pewnym potencjalnym polu sił wyrażone we współrzędnych sferycznych mają postać;
Napisać równania kanoniczne Hamiltona tego punktu.
3.2 Sterowanie optymalne - zagadnienie minimalno-czasowe
4.Wiemy, że równanie stanu pewnego układu ma postać ![]()
oraz ![]()
.Wyznaczyć sterowanie przeprowadzające ten układ z danego stanu początkowego do stanu zerowego w minimalnym czasie.
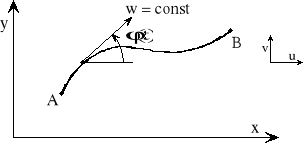
5. Statek płynie w płaszczyźnie xy przez obszar z silnymi prądami. Prąd ma składowe prędkości u(x, y) w kierunku x oraz v(x,y) w kierunku y. Prędkość statku względem wody ma stałą wartość w, zaś kierunek prędkości względnej zadany jest przez kąt φ między wektorem tej prędkości i osią x (rys.). Traktując statek jako punkt materialny, a kąt φ jako sterowanie, sformułować warunki potrzebne do wyznaczenia takiego prawa sterowania, aby czas przepływu z punktu A do punktu B (z góry danych) był minimalny. Następnie przy założeniu, że składowe prędkości nie zależą od współrzędnej y, wyznaczyć konkretne prawo sterowania statkiem.
Wskazówki:
1. w zadaniu tym równanie stanu można uzyskać wyłącznie na podstawie relacji kinematycznych.
2. zastosować ZMP w wersji bez ograniczenia na sterowanie; wówczas dla sterowania optymalnego można przyjąć, że ![]()
.
3.3 Sterowanie optymalne - zagadnienie liniowo-kwadratowe
6. Dane jest równanie ruchu obiektu
![]()
gdzie: T - stała czasowa, zaś γ- współczynnik wzmocnienia obiektu .
Za pomocą techniki Riccatiego należy wyznaczyć sterowanie tego obiektu, które minimalizuje wskaźnik jakości
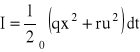
gdzie współczynniki q i r są danymi liczbami dodatnimi.
7. Wyznaczyć strategię sterowania, które przeprowadzi układ opisany równaniem
![]()
ze stanu x(0) = x0 do stanu x(1) = 0 i zminimalizuje przy tym wskaźnik jakości
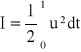
Zastosować technikę Riccatiego