Duże przedsiębiorstwo przemysłowe prowadzi produkcję w 5 zakładach
zlokalizowanych w 5 różnych miejscowościach na terenie kraju.

Do produkcji zużywa surowce, materiały, części i podzespoły zmagazynowane w trzech miejscowościach
.

Odległości [km] pomiędzy zakładami a magazynami podane zostały na schemacie 1;

Schemat 1. Odległości w sieci transportowej

Magazyny dysponują zasobami niezbędnymi do prowadzenia produkcji w zakładach, odpowiednio;
.

Zapotrzebowanie zakładów na materiały, surowce, części i podzespoły jest odpowiednio równe;
.

Rzeczywiste koszty jednostkowe transportu nie są proporcionalne do odległości pomiędzy punktami sieci transportowej, mierzonych w kilometrach. Taryfa przewozowa w tabeli 1:

Odległość [km]	Koszt transportu 1 tony ładunku [EUR]	Odległość [km]	Koszt transportu 1 tony ładunku [EUR]
0 - 25	7,55	521 - 540	34,84
101 - 105	13,74	541 - 560	35,60
136 - 140	16,15	561 - 580	36,36
251 - 260	22,22	581 - 600	38,50
341 - 350	26,79	601 - 620	41,12
371 - 390	28,23	621 - 640	41,72
391 - 400	29,86	641 - 660	45,22
401 - 420	29,86	661 - 680	47,56
421 - 440	30,71	681 - 700	48,73
441 - 460	31,56	701 - 800	50,34
481 - 500	33,27	801 - 900	51,81
501 - 520	34,08	901 - 1000	61,51

Przy odległościach ponad 1000 km, koszt przewozu jednej tony 82 EUR

Tabela 1. Odległości pomiędzy magazynami i zakładami produkcyjnymi.

Wyznaczyć taki plan przewozów zasobów niezbędnych do produkcji, który zaspokoi potrzeby zakładów produkcyjnych a jednocześnie minimalizuje łączny koszt transportu zasobów.

Rozwiązanie:

Odległości w [km] sieci transportowej:

	O1	O2	O3	O4	O5	Zasoby /Oo/
D1	961	400	1.824	344	257	210
D2	481	1.282	723	1.098	425	160
D3	522	1.444	632	381	982	80
Zapotrzeb.	80	60	100	100	60

Koszty jednostkowe [EUR] w sieci transportowej:

	O1	O2	O3	O4	O5	Zasoby /Oo/
D1	61.51	29,86	82	26,79	22,22	210
D2	33,27	82	50,34	82	30,71	160
D3	34,84	82	41,72	28,23	61,51	80
Zapotrzeb.	80	60	100	100	60

Model zagadnienia transportowego

i

j

minimum funkcji
,

gdzie:
- wielkość zasobu dostarczana przez i - tego dostawcę j - temu odbiorcy,

- koszt jednostkowy alokacji zasobu pomiędzy i - tym dostawca a j - tym odbiorcą

Algorytm Forda - Fulkersona

1. Sprowadzenie modelu do zagadnienia „domkniętego” tj. takiego, gdy
   ,

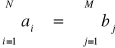
gdzie:
- zasoby i - tego dostawcy,

i

- potrzeby j - tego odbiorcy

j

A. jeśli
, warunek ten oznacza nierównowagę z przewagą zasobów /podaży/, zagadnienie zostanie domknięte, jeśli do sieci transportowej wprowadzony zostanie fikcyjny odbiorca, o skali potrzeb równej
,

B. jeśli
, warunek oznacza przewagę popytu odbiorców nad podażą dostawców, domknięcie zagadnienia, nastąpi w wyniku wprowadzenia do sieci fikcyjnego dostawcy, o zasobach równych
.

2. Wyznaczenie pierwszego rozwiązania dopuszczalnego zagadnienia:

Niech:

C =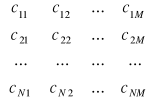
jest macierzą kosztów jednostkowych /”odległości czasowych”, itd./, elementy macierzy przekształcamy według następujących dwu reguł:

1. dla każdego k - tego wiersza wyznaczamy element minimalny
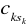
   , gdzie s jest jedną z wartości należących do zbioru {1, 2, … M}, od elementów każdego wiersza odejmujemy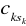
   :

=
,

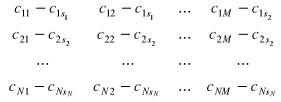
2. dla każdej l - tej kolumny macierzy
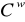
   wyznaczamy element minimalny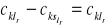
   , gdzie r jest jednym z elementów zbioru {1, 2, … N}, od elementów każdej kolumny odejmujemy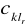
   :

=
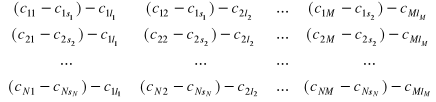
, charakterystyczne

dla macierzy
jest to, że w każdym wierszu i każdej kolumnie otrzymujemy przynajmniej jedną wartość równą zero, macierz
jest macierzą kosztów nazwijmy pozornych /odległości pozornych/.

4. Decyzje o alokacji zasobu na trasy o zerowych wartościach kosztów pozornych, nie zwiększa tzw. kosztu pozornego będącego iloczynem
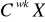
   . Pierwsze rozwiązanie dopuszczalne oparte jest na alokacji zasobu o takich właściwościach. Jeśli w procesie alokacji zostaje rozdysponowany cały zasób, rozwiązanie dopuszczalne jest rozwiązaniem optymalnym. W przeciwnym przypadku należy zwiększyć możliwości alokacji nierozdysponowanego zasobu, poprzez oznaczenie tras, na których alokacja zwiększa wartość pozorną kosztu - trasy nasycone, oraz identyfikację tras, na których alokacja nie zwiększa kosztu pozornego, jest to możliwe w rezultacie realizacji procesu oznaczania.

5. Oznaczanie:

1. każdy wiersz z zasobem różnym od zera /
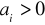
   / oznaczamy /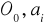
   /,

2. w oznaczonym wierszu identyfikujemy trasy z zerową wartością kosztu pozornego
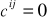
   , wiersz odpowiadający tej wartości kosztu oznaczamy /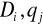
   /, gdzie:

,

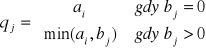
3. w oznaczonych kolumnach identyfikujemy koszty
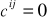
   oraz odpowiadające trasie alokacji (i, j), zasób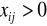
   , tak zidentyfikowane trasy pozwalają oznaczyć wiersze /tylko te, które nie są oznaczone/, oznaczenie /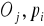
   /, gdzie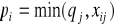
   ,

proces oznaczania jest kontynuowany do momentu, w którym proces oznaczania nie powoduje oznaczenia nowych wierszy oraz kolumn, ogranicza się do tras już oznaczonych,

4. brak możliwości oznaczenia nowych tras otwiera możliwość identyfikacji nowych tras alokacji, tę możliwość uzyskujemy w wyniku „wykreślenia” z tablicy transportowej kolumn oznaczonych i nieoznaczonych wierszy, spośród elementów niewykreślonych wybieramy element minimalny, który odejmujemy od elementów niewykreślonych i dodajemy do elementów podwójnie wykreślonych, w rezultacie otrzymujemy co najmniej jedną trasę z kosztem pozornym równym zero, co identyfikuje trasę alokacji nie zwiększającą kosztu pozornego, w rezultacie alokacji zasobu na zidentyfikowane nowe i dotychczasowe trasy, którym odpowiadają pozorne koszty równe zero, otrzymujemy nowe rozwiązanie dopuszczalne, jest ono optymalne jeśli pozwala rozdysponować cały zasób, zaspokajając jednocześnie potrzeby odbiorców, jeśli rozwiązanie nie ma takiej właściwości, należy powtórzyć procedurę opisaną w punktach I - IV.

	O1	O2	O3	O4	O5	Of	Zasoby /Oo/
D1	61,51	29,86	82	26,79	22,22	0	210
D2	33,27	82	50,34	82	30,71	0	160
D3	34,84	82	41,72	28,23	61,51	0	80
Zapotrzeb.	80	60	100	100	60	50
	O1	O2	O3	O4	O5	Of	Zasoby /O0/
D1	61,51	29,86	82	26,79	22,22	0	210
D2	33,27	82	50,34	82	30,71	0	160
D3	34,84	82	41,72	28,23	61,51	0	80
Zapotrzeb.	80	60	100	100	60	50
	33,27	29,86	41,72	26,79	22,22
	O1	O2	O3	O4	O5	Of	Zasoby /O0/
D1	28,24	0	40,28	0	0	0	210
D2	0	52,14	8,62	55,21	8,49	0	160
D3	1,57	52,14	0	1,44	39,29	0	80
Zapotrzeb.	80	60	100	100	60	50
	O1	O2	O3	O4	O5	Of	Zasoby /O0/
	28,24	0	40,28	0	0	0
D1		60		100	50		0
	0	52,14	8,62	55,21	8,49	0
D2	80					50	30		/Oo; 30/
	1,57	52,14	0	1,44	39,29	0
D3			80				0
Zapotrzeb.	0	0	20	0	10	0
	/D2; 30/					/D2; 30/
	O1	O2	O3	O4	O5	Of	Zasoby /O0/
	36,73	0	40,28	0	0	8,49
D1		60		100	50		0
	0	43,65	0,13	46,72	0	0
D2	80				10	50	20		/Oo; 30/
	10,06	52,14	0	1,44	39,29	8,49
D3			80				0
Zapotrzeb.	0	0	20	0	0	0
					/D2; 10/	/D2; 30/
	O1	O2	O3	O4	O5	Of	Zasoby /O0/
	36,73	0	40,28	0	0	8,49
D1		60		100	50		0		/O5; 20/
	0	43,65	0,13	46,72	0	0
D2	80				10	50	20		/Oo; 20/
	10,06	52,14	0	1,44	39,29	8,49
D3			80				0
Zapotrzeb.	0	0	20	0	0	0
	/D2; 20/	/D1; 20/		/D1; 20/	/D2; 20/	/D2; 20/
	O1	O2	O3	O4	O5	Of	Zasoby /O0/
	36,73	0	40,15	0	0	8,49
D1		60		100	50		0
	0	43,65	0	46,72	0	0
D2	80		20		10	50	0		/O0; 20/
	10,19	52,27	0	1,57	39,42	8,62
D3			80				0
Zapotrzeb.	0	0	0	0	0	0
			/D2; 20/

X =

[723]

M₃

Z₃

Z₄

Z₁

[502]

[522]

[632]

Z₂

M₂

M₁

Z₅

[481]

[922]

[617]

[344]

[400]

[857]

[425]

[257]

[381]

---