46Definicja i równanie toru cząstki
torem elementu płynu nazywamy krzywą opisaną przez poruszającą się cząstkę
element toru:
d r(dx,dy,dz) ,
dt- czas potrzebny na przebycie drogi dr,
wówczas:
dr/dt=r(t)= V(x,y,z,t)
dx/Vx(x,y,z,t)=dt dla y i z tak samo. dt-> jest tutaj zmienna niezależną ( taką samą)
w równaniu tym czas występuje jako parametr, od którego zależą wartość Vx, Vy,Vz
Każdy tor jest związany z jednym elementem płynu.
47Definicja i równanie linii prądu
Równanie lini prądu: wyrażające warunek równoległości wektorów V i dr w każdym punkcie pola dla dowolnej chwili, możemy zapisać w postaci:
W mechanice płynów linia styczna w każdym punkcie do kierunku prędkości cząstki płynu. Linie prądu są liniami wektorowego pola prędkości płynu.
Wektory prędkości płynu są zawsze styczne linii prądu. Wyraża to tzw. równanie linii prądu:
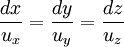
gdzie: ux=Vx, uy=Vy, uz=Vz są składowymi wektora prędkości płynu w kartezjańskim układzie współrzędnych(x,y,z) .
Porównanie toru i lnii prądu: Każdy tor jest związany z 1 elementem płynu, natomiast linia prądu wskazuje prędkość różnych cząsteczek w tej samej chwili.
punkt osobliwy- punk w którym przecina sie kilka ( nieskońzenie wiele) lini prądu
punkt krytyczny- punkt na lini prądu w którym linia prądu ma prędkość równą zero.
Jeżeli przez zamknięty kontur poprowadzimy linie prądu, to w rezultacie otrzymamy powierzchnię prądu zwaną rurką prądu
struga prądu- zbiór lini prądu wypełniających w sposób ciągły rurkę prądu
Elementarna struga prądu- taka struga, której pole przekroju poprzecznego jest nieskończnie małe.
48Pojęcie ruchu potencjalnego i wirowego, 49 równanie lini wirowej
ruch potencjalny:
przepływ potencjalny - jest to przepływ, gdzie rot V=W=2w=0
Analityczny warunek:
δVz/δy=δVy/δz, δVx/δz=δVz/δx, δVy/δx=δVx/δy
powyższe warunki powodują istnienie w obszarze bezwirowego przepływu pewnej funkcji
ϕ (x,y,z), wzglednie ϕ(x,y,z,t) 0 dla przepływu nieustalonego, takiej , żę:
Vx=δ ϕ/δx itd.
czyli V=grad ϕ
W każdym punkcie pola potencjał prędkośći ma zazwyczaj inna wartość. Całkowita zmiana potencjalu dwóch sąsiednich cząsteczek jest określona różniczką zupełna d ϕ, czyli
dϕ= δϕ/δx *dx + δϕ/δy * dy+δϕ/δz *dz
miejsce gdzie d ϕ=0 -> powierzchnia jednakowego potencjału.
dϕ=Vx*dx+Vy*dy+Vz*dz
ruch wirowy:
składowe prędkości kątowej są różne od zera
ωx=/0, ω y=/0 ,ω z=/0 , gdzie ω = małe omega ( brak symbolu !!)
ruch wirowy jest określony polem wektorowym prędkośći kątowej chwilowego obrotu w zwanym polem wirowym.
z polem wirowym wiąże się: pojęcie
a)lini wirowej- linia pola wektorowego rotacji rot V = 2 ω = W <-wszystko wektory
wektor wiru jest równy podwojonemu wektorowi prędkośći katowej obrotu elementu płynu i podobnie jak w jest wektorem leżącym stale na chwilowej osi obrotu elementu.
równanie linii wirowej:
podobnie jak linie prądu tworzą powierzchnie prądu, tak linie wirowe tworzą powierzchnię. taka ( płąszczyzna przecinająca prostopadle )
b)rurki wirowej-
Jeżeli przez każdy punkt krzywej zamkniętej poprowadzimy linie wirowe, to linie te utworza rurke wirowa.
nieskończneie mała rurka wirowa tworzy elementarną rurkę wirową
Rurka wirowa wraz z liniami wirowymi znajdującymi się wewnątrz niej nazywa się strugą wirową. Jeżeli krzywa jest zamknięta nieskończenie małym konturem, linie wirowe przechodzprzez ten kontur tworzą elementarną strugę wirową/
51Równanie ciągłości ruchu jednowymiarowego i ogólnego (niedokończone)
należy się tu oprzeć na zasadzie zachowania masy. W płynie nieściśliwym (p=const) tylko takie pole prędkośći będzie spełniało tę zasadę, w którym w każdej chwili do obszaru ograniczonego powierzchnia kontrolna będzie wpływało tyle płyniu, ile w tej samej chwili wypływa.
Warunek ten jset zatem identyczny dla przepływów ustalonych i nieustalonych.
Dla płyny ściśliwego: również jest zachowanu warunek zachowania masy, dla przepływu ustalonego, bo masa zawarta wewnatrz powierzchni kontrolnej jest niezmienna w czasie.
Dla przepływu nieustalonego: z upływem czasu gęstość moze ulegać lokalnym zmianom, co może wywołąć zmianę masy płynu objętej powierzchnią kontrolną.
52Równanie Bernoulliego ruchu jednowymiarowego
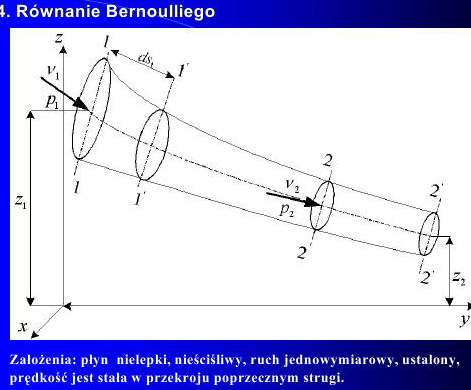
Ec= Ep + E p' + Ek
Energia potencjalna polożenia
Ep= dm g z1= ρ * V gz1= ρ* A*ds*g*z1=ρ*A*v*dt*g*z1=ρQdt g z1
Energia potencjalna ciśnienia:
Ep=F*ds=p*dA*ds=p*Q*dt
Energia kinetyczna
Ek=(mv^2)/2 = 1/2(ρ*V ) *v^2= 1/2(ρ* ds*A)*v^2=1/2* (ρ *Q dt) v^2
Ec1=Ep1+Epp1+Ek1
Ec2=Ep2+Epp2+Ek2
Ec1=Ec2
ρgz1+p1+ρ(v1^2)/2=ρgz2+p2+ρ(v2^2)/2
postać wysokościowa:

53. Interpretacja graficzna równania Bernoulliego
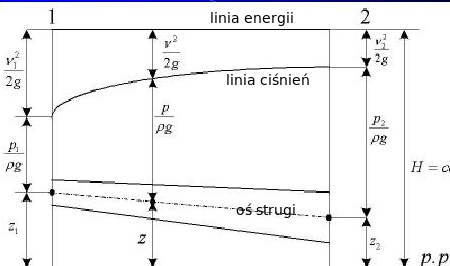
Linai energii jest linia prosta zgodnie z zależnoscia z+ p/ρg + V^2/2g = H = const.
Przebieg osi strugi i lini ciśnień natomiast zależy od położenia strugi względem poziomu odniesienia oraz kształtu strugi.
56 Rurka Prandtla - schemat, przeznaczenie, wzory obliczeniowe
Rurka Prandtla - przyrząd do pomiaru prędkości przepływu płynu poprzez pomiar ciśnienia w przepływającym płynie (cieczy oraz gazów).
Składa się on z dwóch osadzony w sobie rurek, z czego pierwsza wewnętrzna służy do badania ciśnienia całkowitego płynu, natomiast zewnętrzna do badania ciśnienia statycznego.
Rurka poprzez otworek na półkulistym nosku rurki mierzy ciśnienie całkowite p1 (ciśnienie spiętrzenia), a poprzez otwór w powierzchni bocznej oddalony od przodu rurki, ciśnienie statyczne p2.


57 Pomiar strumienia przepływu metodą zwężkową
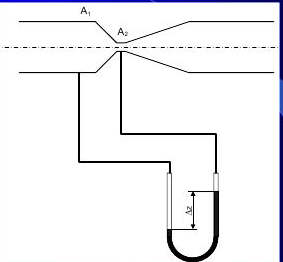
Rozpisujemy tu równanie Bernouliego, przyjmując poziom porównawczy z linia przerywaną
v2=[2(p2-p1)/ρ(1-(d2/d1)^2)]^1/2
oraz Równanie ciągłości
A1*v1=A2*V2
58. Prędkość wypływu cieczy przez mały otwór

59. Zjawisko kontrakcji strugi, współczynniki prędkości, kontrakcji i wypływu
kontrakcja strumienia: obserwując strumień wypływający przez otwór ostro bieżny, stwierdzamy, że pole przekroju strumienia Ac w pewnej odległości (na ogół równej ½ średnicy otworu) od otworu wylotowego jest mniejszy od pola otworu A. Zjawisko to powodują siły bezwładność
współczynnik kontrakcji: ϰ=Ac/A - zależy od liczby reynoldsa, kształtu i usytuowania otworu wypływowego
współczynnik prędkości : φ=vr/v , gdzie Vr- prędkość rzeczywista, V- teoretyczna prędkość
współczynnik wypływu: Rzeczywiste natężenie wypływu obliczamy z zależnosci:
Q=vr*Ac= φv * ϰ A=μ vA μ=φϰ <-współczynnik wypływu.
Wyszukiwarka
Podobne podstrony:
mechanika plynow opracowanie zagadnien
mechanika plynow opracowane zagadnienia (2), Sprawka
mechana plynow opracowane zagadnienia kolo1, PG inżynierka, Semestr 3, Mechanika płynów, wykład
mechanika płynów opracowanie
Mechanika płynów opracowane zagadnienia, Inżynieria Środowiska-Szczecin, Mechanika płynów, Wykłady+k
Mechanika płynów opracowanie
mechanika plynow opracowanie
mechana plynow opracowane zagadnienia, OiO sem. III, mechanika płynów
Mechanika plynow opracowanie
Mechanika plynow opracowanie wersja zmniejszona
mechanika plynow opracowanie zagadnien
mechanika plynow opracowanie
Mechanika Techniczna I Opracowanie 06
Mechanika gruntów opracowanie na egzamin
9048000196926-mechanika techniczna opracowane pytania maruszewski-ulepszone, 1
więcej podobnych podstron