1. Jakie podstawowe właściwości odróżniają płyny od ciał stałych?
–

Ciała stałe przenoszą obciążenia zewnętrzne w taki sposób, że ulegają deformacji tak długo
jak długo działa siła, po ustąpieniu siły powracają do stanu poprzedniego (o ile nie
przekroczono granicy plastyczności)

–

Płyny pod działaniem obciążenia zewnętrznego ulegają ciągłemu odkształceniu i nie
powracają do stanu poprzedniego po ustąpieniu siły

–

Płyny nie mają „własnego” kształtu tak jak ciała stałe – przyjmują kształt naczynia w
którym są umieszczone, przy czym gazy wypełniają całe naczynie, a ciecze tworzą
swobodne powierzchnie, oddzielające je od gazów lub próżni.

2. W jakich warunkach płyn pozostaje w stanie równowagi?

Płyn jest w równowadze pod działaniem danych sił zewnętrznych jeżeli siły działające na każdą
dowolnie ograniczona jego część tworzą układ wektorów równoważny zeru.

Warunki równowagi płynu:
Jednostkowa siła masowa:



F = X iY jZ k=F  x , y , z 

Gęstość:

=

x , y , z

Warunki równowagi elementu płynu:

X  dxdydz pdydz− p

∂ p

∂ x

dx  dydz=0

Y  dxdydz pdxdz− p

∂ p

∂ y

dy dxdz=0

Z  dxdydz pdxdy− p

∂ p

∂ z

dz  dxdy=0

stąd otrzymujemy:

X =

1


∂ p

∂ x

y=

1



∂ p

∂ y

Z =

1



∂ p

∂ z

Co prowadzi do podstawowego w hydrostatyce Równanie Eulera:



F =

1


rot p

lub w postaci różniczkowej:

XdxYdyZdz =

dp



jeżeli pole sił masowych ma potencjał U, czyli:



F =−grad U

to otrzymamy:

dU =

dp



i po scałkowaniu:

p=− U C

Stała całkowania może być wyznaczona ze znanego ciśnienia i potencjału sił masowych w
określonym punkcie obszaru płynu.

3. Od jakich wielkości zależy napór hydrostatyczny na płaską ścianę zbiornika wypełnionego

cieczą?

Napór całkowity na ścianę płaską:



P= g

∫

S

n zdS = g 

n

∫

S

zdS = g n z

C

S

gdzie:

z

C

- zanurzenie środka geometrycznego ściany S

Wniosek:
Napór hydrostatyczny na ścianę płaską o dowolnym konturze i dowolnie nachyloną do poziomu jest
równy (co do modułu) ciężarowi słupa cieczy o podstawie równej polu S i wysokości
równej zanurzeniu jej środka geometrycznego pod swobodną powierzchnią.

Napór na ścianę o dowolnym kształcie:
Rzut naporu na dowolny kierunek poziomy jest równy naporowi całkowitemu wywieranemu na

ścianę płaską której pole jest równe rzutowi pola ściany zakrzywionej na płaszczyznę pionową
prostopadłą do danego kierunku.

Rzut naporu na kierunek pionowy jest równy ciężarowi słupa cieczy zawartego pomiędzy ścianą S a
jej rzutem na swobodną powierzchnię.

4. Czym różni się ruch ogólny płynu od ruchu ogólnego ciała sztywnego?

Ruch ogólny ciała sztywnego można przedstawić jako sumę przemieszczenia liniowego i obrotu.
Ponieważ płyny nie mają sztywności postaciowej, w ruchu płynu dochodzi dodatkowo do
odkształcenia elementu płynu.

Ruch ogólny elementu płynu można więc traktować jako superpozycję
przemieszczenia liniowego (translacji), obrotu względem chwilowego bieguna
oraz odkształcenia (deformacji), które z kolei można podzielić na liniowe
(objętościowe) i kątowe (postaciowe).

5. Przedstaw równanie zachowania masy w przepływie płynu nieściśliwego przez rurociąg o

zmiennym przekroju

Prawo zachowania masy: w zamkniętym układzie fizycznym masa nie może powstać ani nie może
ulec anihilacji.

 u S =const

, gdzie

−średnia gęstość u−średnia prędkość płynu

Wnioski:

–

w ustalonym przepływie płynu ściśliwego natężenie przepływu masy (strumień masy) przez
każdy poprzeczny przekrój rurki prądu jest stałe

–

w ustalonym przepływie płynu nieściśliwego objętościowe natężenie przepływu (strumień
objętości) jest stałe, czyli prędkość przepływu jest odwrotnie proporcjonalna do pola
przekroju rurki prądu.

6. Jaką zasadę fizyczną opisuje równanie Naviera-Stokesa?

Podstawienie zależności wynikających z modelu płynu Newtona do równania zachowania pędu
daje równanie znane jako równanie Naviera-Stokesa.
(Płyn Newtonowski – nieściśliwy płyn lepki.)



Du

D t

= 

f − gradp grad  divudiv 2 [ D]

A= BC DE

A – prędkość zmiany pędu elementu płynu
B – siła masowa
C – siła powierzchniowa ciśnienia
D – siła powierzchniowa związana z lepkością płynu, wynikająca ze zmiany objętości elementu
płynu ściśliwego (kompresji lub ekspansji)
E- siła powierzchniowa związana z lepkością płynu, wynikająca z deformacji liniowej i postaciowej
elementu płynu

7. Napisz równanie Bernoulliego i przedstaw interpretację fizyczną jego wyrazów.

Założenia:

-przepływ jest stacjonarny

∂

∂ t

=

0

-plyn jest nielepki

=

0

-płyn jest barotropowy

=

p

-pole sił masowych jest potencjalne

f =−grad 

Przy takich założeniach można scałkować równanie Eulera:



Du

Dt

= 

f − grad p

Otrzymujemy:

grad [

u

2

2



P  p]=grad E=rot u×u

Wyrażenie w nawiasie nazywamy trójmianem Bernoulliego. Można wykazać stałość tego trójmianu
w pięciu przypadkach:

1) wzdłuż linii prądu
2) wzdłuż linii wirowej
3) w przepływie bezwirowym
4) w przypadku hydrostatycznym
5) w przepływie śrubowym

Równanie Bernoulliego:

gz

p





u

2

2

=

const

lub

z 

p



g



u

2

2g

=

const

Suma energii potencjalnej pola sił masowych, energii ciśnienia oraz energii kinetycznej płynu jest
stała.

lub:

Suma wysokości geometrycznej, wysokości ciśnienia (czyli wysokości, na jaką wzniesie się słup
cieczy pod ciśnieniem p) oraz wysokości prędkości (czyli wysokości, z której spadający element
płynu uzyska prędkość u) jest stała.

8. Przedstaw interpretację fizyczną następujących kryteriów podobieństwa przepływów: liczby

Strouhala, liczby Eulera, liczby Froude,a i liczby Reynoldsa.

Sh−liczba Strouhala

Sh=

l

tu

=

t

c

t

t

c

- czas charakterystyczny przepływu (czyli czas pokonania przez płyn charakterystycznego

wymiaru liniowego l – np. długości rurociągu, z prędkością charakterystyczną u)
t - czas zmienności niestacjonarnych warunków przepływu, np. długość cyklu pracy pompy
tłokowej
Mała wartość liczby Strouhala w danym przepływie oznacza, że niestacjonarne zjawiska w tym
przepływie są mało istotne i mogą być pominięte.

Fr−liczba Froude ' a



Fr 

2

=

u

2

fl

Liczba Froude’a wyraża stosunek sił bezwładności do sił masowych

Eu−liczba Eulera

Eu=

p



u

2

Liczba Eulera wyraża stosunek sił ciśnienia do sił bezwładności

ℜ=



u l



=

ul



Liczba Reynoldsa wyraża stosunek sił bezwładności do sił lepkości .

Ec−liczba Eckerta

Ec=

u

2

cT

Liczba Eckerta wyraża stosunek energii kinetycznej makroskopowego ruchu płynu do energii ruchu

molekularnego (energii wewnętrznej) płynu.

Pr−liczba Prandtla

Pr =

c 



Liczba Prandtla wyraża stosunek intensywności transportu pędu płynu do intensywności transportu
energii płynu
Liczba Prandtla jest jedyną liczbą kryterialną składającą się tylko ze
stałych materiałowych.

9. Scharakteryzuj przepływy laminarne i przepływy turbulentne.

Przy niskich wartościach liczby Reynoldsa, czyli przy relatywnie dużych siłach lepkości, przepływ
ma charakter uporządkowany – elementy płynu poruszają się po torach równoległych i nie dochodzi
do ich wzajemnego mieszania się. Przepływ taki nazywamy laminarnym czyli uwarstwionym.
Powyżej pewnej wartości liczby Reynoldsa (zwanej dolną liczbą krytyczną), na skutek rosnącej roli
sił bezwładności przepływ taki traci stateczność i pojawiają się w nim zaburzenia charakteryzujące
się stochastycznymi fluktuacjami prędkości.
Przy dalszym wzroście liczby Reynoldsa (powyżej tzw. górnej wartości krytycznej) zaburzenia
obejmują cały przepływ, który wtedy jest nazywany turbulentnym.

Przepływ laminarny – uporządkowany ruch płynu po torach równoległych, elementy płynu nie
mieszają się ze sobą, działa czysto lepkościowy mechanizm wymiany pędu i energii
Przepływ turbulentny – chaotyczny ruch płynu o stochastycznym charakterze, niestacjonarny
nawet przy ustalonych warunkach brzegowych, elementy płynu mieszają się ze sobą, co prowadzi
do intensyfikacji wymiany masy, pędu i energii.

10. Co to jest warstwa przyścienna? W jakich warunkach może dojść do oderwania warstwy

przyściennej?

Warstwa przyścienna jest to część obszaru przepływu bezpośrednio sąsiadująca z powierzchnią
opływanego ciała. W warstwie przyściennej znaczącą rolę odgrywają siły lepkości i występują tam
znaczne poprzeczne gradienty prędkości przepływu. Poza warstwą przyścienną przepływ może być
praktycznie uważany za nielepki. Za opływanym ciałem warstwa przechodzi w tzw. ślad.
Umowną grubość warstwy



określa osiągnięcie prędkości

u=0,99 u

∞

Wystąpienie dodatniego gradientu ciśnienia wzdłuż warstwy przyściennej (czyli wzrostu ciśnienia
w kierunku przepływu), może prowadzić do tzw. oderwania warstwy przyściennej.

Oderwanie może wystąpić zarówno w laminarnej jak i w turbulentnej warstwie przyściennej (w
turbulentnej występuje później, czyli przy wyższym gradiencie ciśnienia). Oderwanie warstwy
przyściennej jest zjawiskiem niekorzystnym, zakłóca pracę maszyn i urządzeń przepływowych oraz
obniża ich sprawność. Maszyny i urządzenia przepływowe powinny być projektowane w taki
sposób, aby unikać oderwania przepływu przynajmniej w ich projektowych warunkach
pracy.

11. Na czym polega zjawisko kawitacji i w jakich warunkach może wystąpić?

Kawitacja jest to zjawisko dynamicznego wzrostu i zaniku pęcherzy parowo-gazowych w cieczy,
wywołane zmianami ciśnienia przy stałej temperaturze.
Parametrem opisującym podobieństwo zjawisk kawitacyjnych jest liczba kawitacyjna σ

=

p− p

v

1
2



U

2

, gdzie

p

v

- ciśnienie krytyczne pary wodnej (ok. 2000 Pa)

Uproszczony warunek kawitacji:

p p

v

Zapoczątkowanie kawitacji polega na destabilizacji mikropęcherzyków stanowiących naturalną

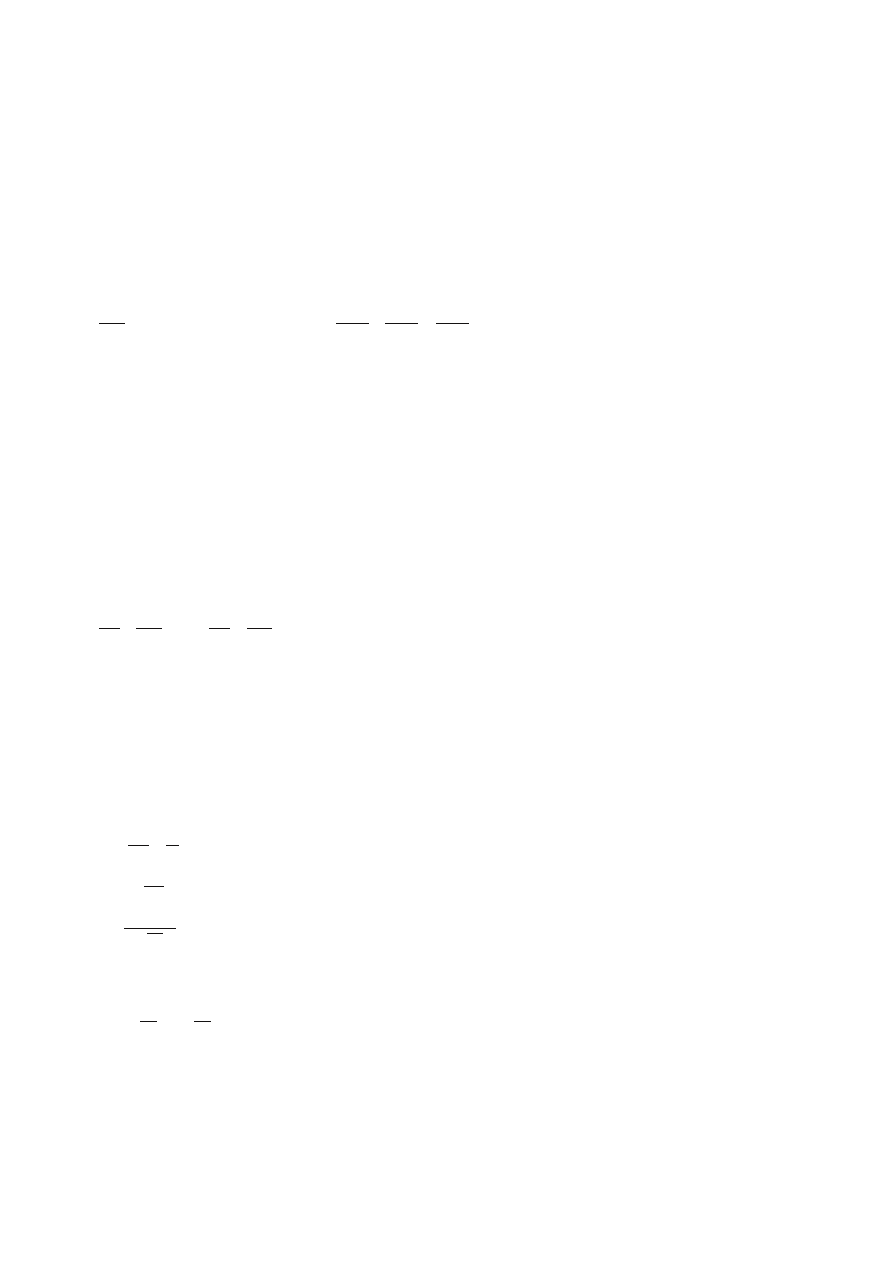
zawartość cieczy .
Formy kawitacji:

–

kawitacja laminarna

–

kawitacja pęcherzykowa

–

kawitacja wirowa

–

kawitacja chmurzasta

12. Co to są przepływy potencjalne i jak mogą być modelowane matematycznie?

Jeżeli przepływ płynu jest bezwirowy, czyli wszędzie lub prawie wszędzie w polu przepływu jest
rotu = 0 to oznacza, że istnieje funkcja skalarna φ (x, y, z ) , taka że u = gradφ . Przepływ taki
nazywamy przepływem potencjalnym, a funkcję φ nazywamy potencjałem prędkości.

∂ p

∂ t



div u=0  divgrad =

∂

2



∂ x

2



∂

2



∂ y

2



∂

2



∂ z

2

=

0

Równanie Laplace’a jest liniowe, co oznacza, że suma jego rozwiązań jest również rozwiązaniem.
W praktyce więc można składać bardzo skomplikowane funkcje potencjału, opisujące złożone
przepływy, z funkcji opisujących tzw. przepływy elementarne.

Elementarne przepływy potencjalne:

–

przepływ jednorodny

–

źródło (dodatnie lub ujemne)

–

źródło podwójne (dipol)

–

wir (jedyny niesymetryczny przepływ elementarny!)

13. W jaki sposób uwzględniane są straty energii płynu w równaniu Bernoulliego opisującym

rzeczywisty przepływ płynu lepkiego przez rurociąg?

u

1

2

2g



p

1



g



z

1

=

u

2

2

2g



p

2



g



z

2



h

s

=

H =const

h

s

−

wysokość strat

Wysokość strat możemy podzielić na dwa składniki:

–

wysokość strat liniowych związanych z tarciem płynu o ścianki przewodu prostoliniowego o
stałym przekroju

–

wysokość strat lokalnych związanych z obecnością zaworów, kolan, zwężeń, rozgałęzień i
innych elementów.

Straty liniowe:

h

s

=

u

2

2g



l

d

=

64

ℜ

dla przepływy laminarnego

=

0,3164

4



ℜ

dla przepływu turbulentnego

Straty lokalne:

h

s

=

u

1

2

2

=

'

u

2

2

2