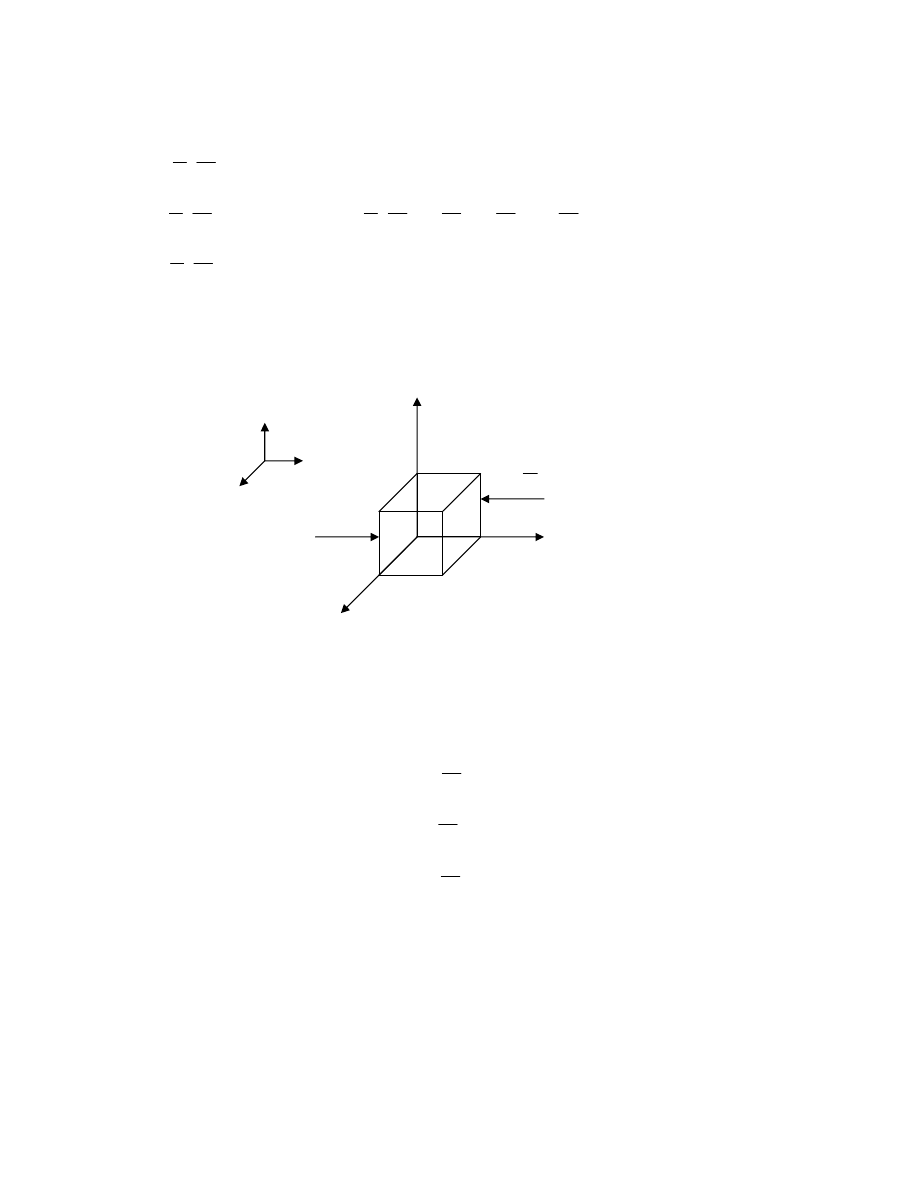
1
1.
Równanie równowagi
z
p
Z
dp
dz
z
p
dy
y
p
dx
x
p
Zdz
Ydy
Xdx
y
p
Y
x
p
X
∂
∂
⋅
=
=
∂
∂
+
∂
∂
+
∂
∂
=
+
+
⇒
∂
∂
⋅
=
∂
∂
⋅
=
ρ
ρ
ρ
ρ
ρ
1
1
1
1
X, Y, Z – siła składowa w określonym kierunku – składowa jednolita
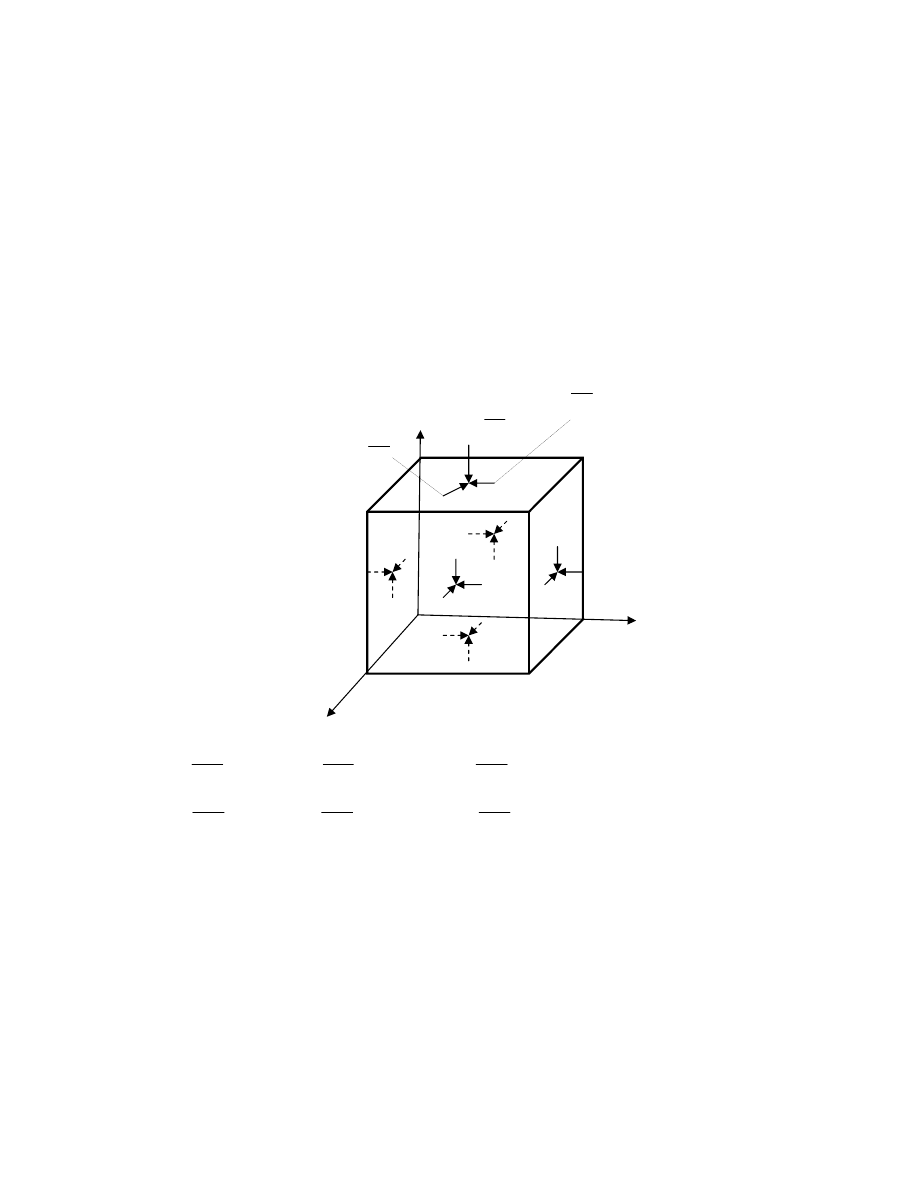
Element płynu dV=dxdydz jest w równowadze, gdy rzuty sił na osie układu są równe 0
0
0
0
=
∂
∂
+
−
+
=
∂
∂
+
−
+
=
∂
∂
+
−
+
dxdy
dz
z
p
p
pdxdy
Zdm
dxdz
dy
y
p
p
pdxdz
Ydm
dydz
dx
x
p
p
pdydz
Xdm
dydz
dx
x
p
p
∂
∂
+
pdydz
z
x
y
dx
dy
dz
Zdm
Xdm
Ydm

2
2.
Zasada działania manometru U-rurkowego
Manometr u-rurkowy służy do pomiaru różnicy ciśnień na podstawie różnicy wysokości
cieczy manometrycznej
1
2
h
h
h
p
m
−
=
=
∆
Dla powierzchni ekwipotencjalnej na poziomie 0, równowaga ciśnień:
2
2
1
1
h
g
p
h
g
h
g
p
m
m
m
ρ
ρ
ρ
+
=
+
+
m
ρ
- gęstość cieczy manometrycznej
ρ
- gęstość mierzonego ośrodka
(
)
m
m
h
g
p
p
p
ρ
ρ
−
=
−
=
∆
2
1
3. Parcie cieczy na ścianę płaską, moment statyczny powierzchni
p
1
p
2
h
m
h
1
h
2
z
N
z
s
z
A
x
n
y
S(x
s
,y
s
)
N
y
N
x
α
F
0
p
a
N – środek parcia
S – środek ciężkości
dF
dA

3
Rozpatrujemy parcie cieczy na powierzchnię A
1
, która jest fragmentem płaskiej ściany
zbiornika
Parcie elementarne wynosi:
zdA
g
dA
p
F
h
ρ
=
=
∆
p
h
– ciśnienie hydrostatyczne
We wzorze pomięto p
a
bo zbiornik jest otwarty.
Ściana zbiornika nachylona jest pod kątem α
F – wypadkowa siła parcia skierowana prostopadle do powierzchni ściany zbiornika jest sumą
parć elementarnych dF
Parcie działa na pow. A o środku ciężkości S
∫∫
∫∫
∫∫
=
⇒
⋅
=
=
=
=
=
A
s
s
A
A
h
ydA
g
F
y
z
A
p
A
z
g
zdA
g
dA
p
F
α
ρ
α
ρ
ρ
sin
sin
p
s
– cieśninie hydrostatyczne na głębokości z
s
A
y
ydA
M
s
A
x
=
=
∫
- Moment statyczny powierzchni A względem osi x, odgrywa rolę w
związku:
x
xo
s
n
M
I
z
z
+
=
, gdzie:
xo
I
- moment bezwładności powierzchni A względem osi x
0
4.
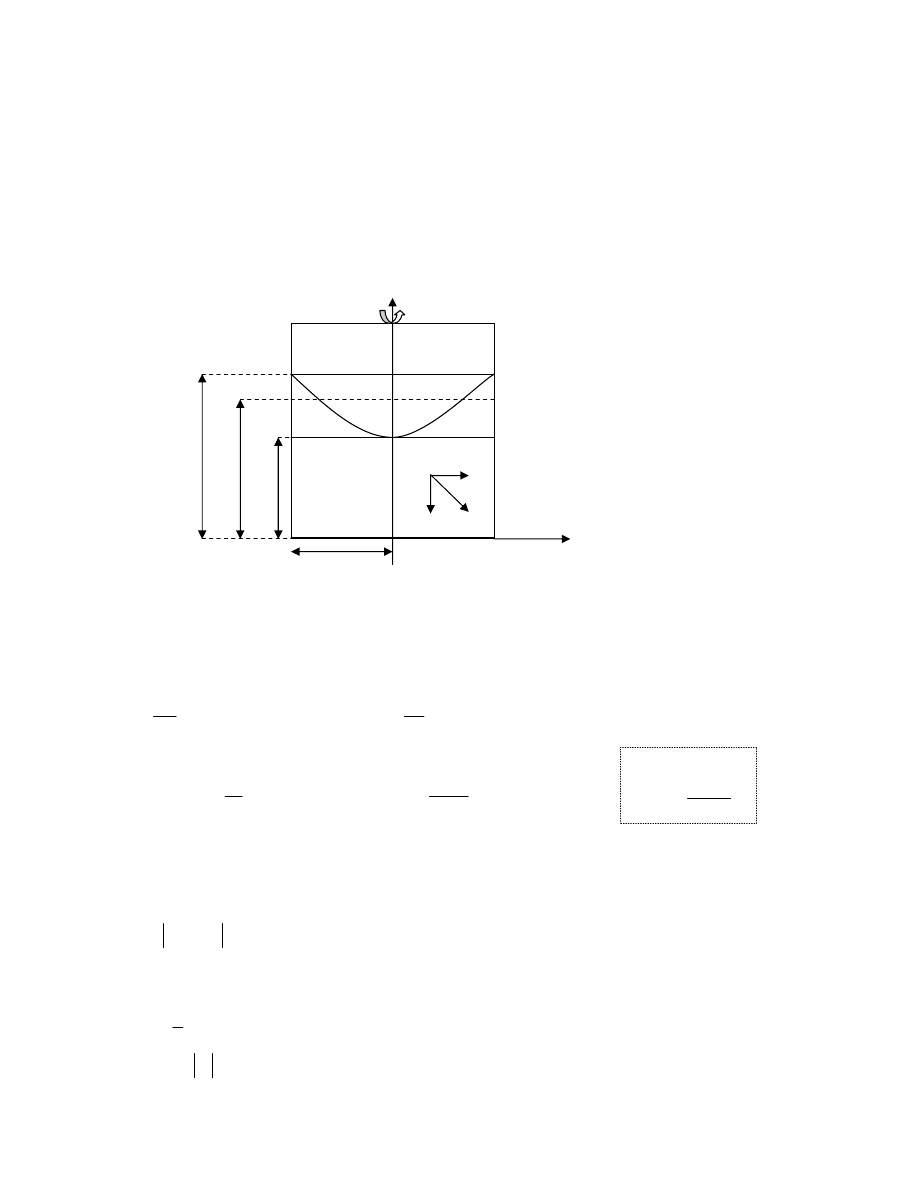
Parcie płynu na ciała zanurzone
Wypadkowa parcia w poziomie = 0. ponieważ siły się równoważą
W kierunku pionowym:
2
1
z
z
z
F
F
F
−
=
F
z1
– parcie do góry równe ciężarowi cieczy nad dolną powierzchnią ciała
F
z2
– parcie do dołu równe ciężarowi cieczy nad górną powierzchnią ciała
Wypadkowa parcia do góry jest równa ciężarowi cieczy o tej samej objętości co objętość
ciała. Wypadkowa skierowana do góry – wypór
V
g
F
W
z
ρ
=
=
Na ciało zanurzone w cieczy działa ciężar ciała G
s
oraz wypór W
s
a) G
s
< W
s
Ciało będzie się wynurzać, aż do momentu gdy część będzie nad lustrem płynu (jak bryły
lodowe). Stan równowagi zostanie osiągnięty, gdy siła wyporu części zanurzonego ciała
będzie równa ciężarowi ciała – ciało będzie pływać
z
x
F
z1
A
x
F
z2
F
x
F
x
4
b) G
s
= W
s
Ciało pływa na dowolnej głębokości – w teorii. W praktyce ustala się głębność pływania na
podstawie różnicy gęstości będącej funkcją temperatury lub ciśnienia zależną od głębokości
zanurzenia.
c) G
s
> W
s
Ciało tonie
5. Ruch obrotowy elementu płynu
ω = const
∫
∫
∫
+
−
=
⇒
−
=
−
=
=
=
c
gz
r
p
gdz
dr
r
dp
g
Z
Y
r
X
2
2
2
2
2
0
ω
ρ
ω
ρ
ω
( )
g
r
z
z
gz
gz
r
p
p
gz
p
c
c
gz
p
a
a
a
a
a
a
a
2
2
2
2
2
ω
ω
ρ
ρ
ρ
+
=
⇒
+
−
+
=
+
=
⇒
+
−
=
6. Niezmienniki tensora symetrycznego
Przez niezmiennik tensora symetrycznego rozumiemy wyrażenie utworzone ze składowych
tensora. Wartość tego wyrażenia nie zmienia się przy przekształcaniu układu współrzędnych.
W celu znalezienie niezmienników należy rozważyć równanie charakterystyczne tensora
symetrycznego.
0
det
=
−
ij
ij
a
ζρ
po rozpisaniu:
(
)
2
12
33
2
31
22
2
23
11
31
23
12
33
22
11
3
2
31
2
23
2
12
11
33
33
22
22
11
2
33
22
11
1
3
2
2
1
3
2
det
2
1
0
a
a
a
a
a
a
a
a
a
a
a
a
a
I
a
a
a
a
a
a
a
a
a
a
a
a
a
I
a
a
a
a
I
I
I
I
ij
ji
ij
jj
ii
ii
−
−
−
+
=
=
−
−
−
+
+
=
−
=
+
+
=
=
=
−
+
−
ζ
ζ
ζ
z
o
z
a
ω
a
-g
r
R
z
z
R
(
)
(
)
g
R
z
z
z
z
z
z
o
a
a
o
a
R
4
2
2
ω
−
=
−
=
−
5
Wyrażenia
3
2
1
,
,
I
I
I
noszą nazwę I, II, III niezmiennika tensora. Wszystkie kombinacje
niezmienników są również niezmiennikami. W szczególnym przypadku gdy I niezmiennik
tensora jest równy 0 nazywamy go dewiatorem. Każdy tensor symetryczny można
przedstawić w postaci dewiatora i tensora kulistego (aksjatora) a
m
ij
kk
ii
m
ij
kk
ij
ij
a
a
a
a
s
δ
δ
δ
3
1
3
1
=
−
=
7. Metoda Lagrange'a do opisywania ruchu płynu
Polega na opisywaniu zmian w czasie wielkości fizycznych lub wektorowych w punkcie
który porusza się wraz z badanym ośrodkiem. Za każdym razem opisujemy ten sam punkt
materialny. Niezbędne jest wybranie konkretnej cząstki – można tego dokonać poprzez
opisywanie jej położenia dla chwili t
0
, a następnie śledzenia jej w czasie t.
W punkcie [1] składowe pola prędkości wynosi
1
x
v
natomiast dla punktu [2]
2
x
v
( ) ( ) ( )
(
)
t
t
z
t
y
t
x
f
v
x
,
,
,
=
Metoda Lagrangea stosowana jest przy opisie układów nieustalonych (zmiennych w czasie),
zmianę pola opisuje pochodna substencjalna (materialna)
z
v
y
v
x
v
dt
dt
d
z
y
x
∂
∂
+
∂
∂
+
∂
∂
+
∂
=
ψ
ψ
ψ
ψ
ψ
Pochodna substencjalna składa się ze składowej opisującej lokalną zmianę w czasie wielkości
ψ
oraz składowej konwekcyjnej zmiany tej wielkości
z
1
z
2
v
x1
v
x2
x
2
y
2
x
1
y
1
x
z
y
1
2
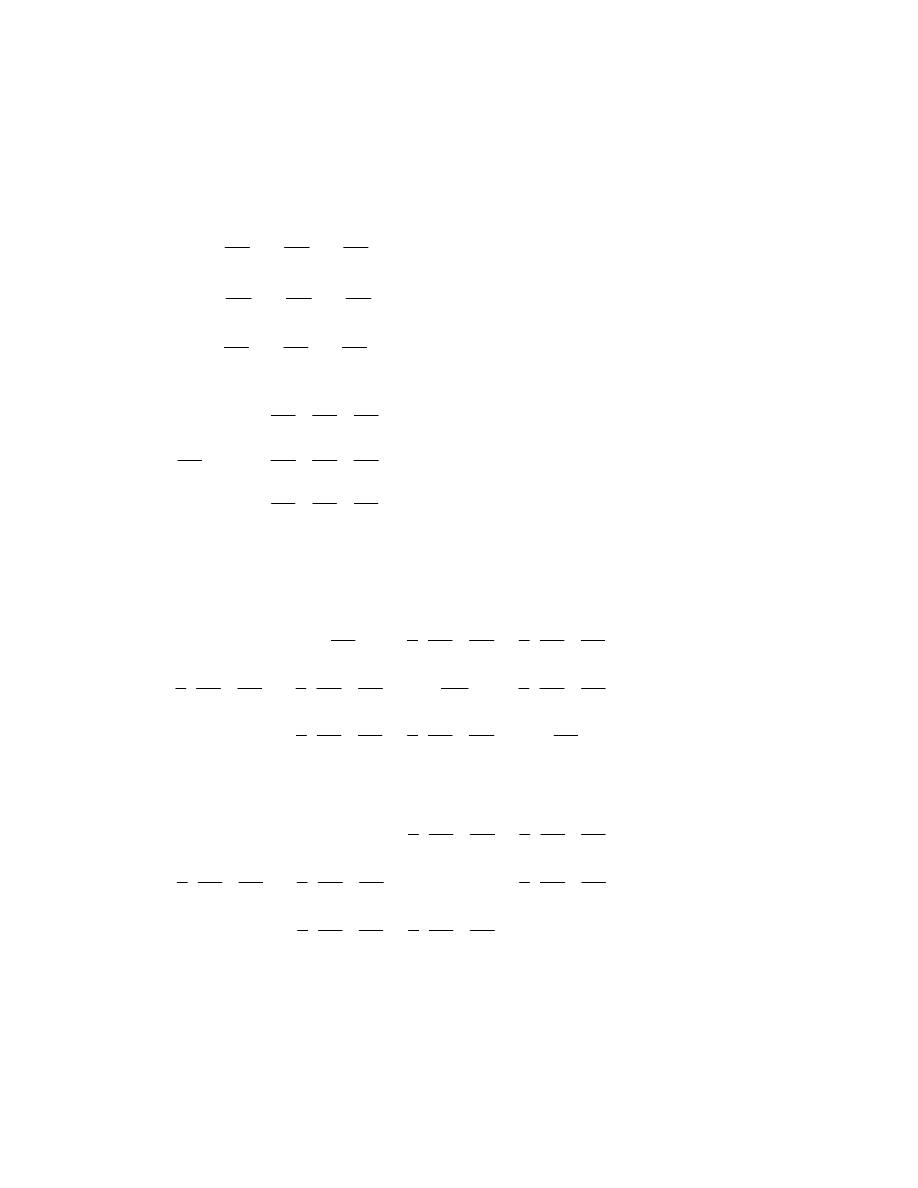
6
8. Odkształcenie elementu płynu, tensor prędkości deformacji, tensor rotacji.
Miarą odkształcenia elementu płynu jest tensor prędkości deformacji d
ij
W chwili t prędkość elementu płynu w pkt O(x,y,z)opisana jest jako:
(
)
(
)
(
)
z
y
x
v
z
y
x
v
z
y
x
v
z
y
x
,
,
,
,
,
,
dla tej samej chwili w punkcie oddalonym o dx, dy, dz prędkość płynięcia wynosi
z
v
dz
y
v
dy
x
v
dx
v
v
z
v
dz
y
v
dy
x
v
dx
v
v
z
v
dz
y
v
dy
x
v
dx
v
v
z
z
z
z
z
y
y
y
y
y
x
x
x
x
x
∂
∂
+
∂
∂
+
∂
∂
+
=
∂
∂
+
∂
∂
+
∂
∂
+
=
∂
∂
+
∂
∂
+
∂
∂
+
=
1
1
1
O deformacji decydują gradienty prędkości, które mogą być zapisane w postacie tensora
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
⇒
∂
∂
=
z
v
y
v
x
v
z
v
y
v
x
v
z
v
y
v
x
v
G
x
v
G
z
z
z
y
y
y
x
x
x
ij
j
i
ij
Tensor ten można rozłożyć na tensor symetryczny i antysymetryczny
a) tensor symetryczny jest tensorem prędkości deformacji i określa odkształcenie elementu
płynu
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
∂
∂
+
∂
∂
=
z
v
z
v
y
v
z
v
x
v
y
v
z
v
y
V
y
v
x
v
x
v
z
v
x
v
y
v
x
v
x
v
x
v
d
z
y
z
x
z
z
y
y
x
y
z
x
y
x
x
i
j
j
i
ij
2
1
2
1
2
1
2
1
2
1
2
1
2
1
b) tensor antysymetryczny określa prędkość kątową obrotu elementu płynu
∂
∂
−
∂
∂
∂
∂
−
∂
∂
∂
∂
−
∂
∂
∂
∂
−
∂
∂
∂
∂
−
∂
∂
∂
∂
−
∂
∂
=
∂
∂
−
∂
∂
=
0
2
1
2
1
2
1
0
2
1
2
1
2
1
0
2
1
z
v
y
v
z
v
x
v
y
v
z
v
y
v
x
v
x
v
z
v
x
v
y
v
x
v
x
v
y
z
x
z
z
y
x
y
z
x
y
x
i
j
j
i
ij
ω
7
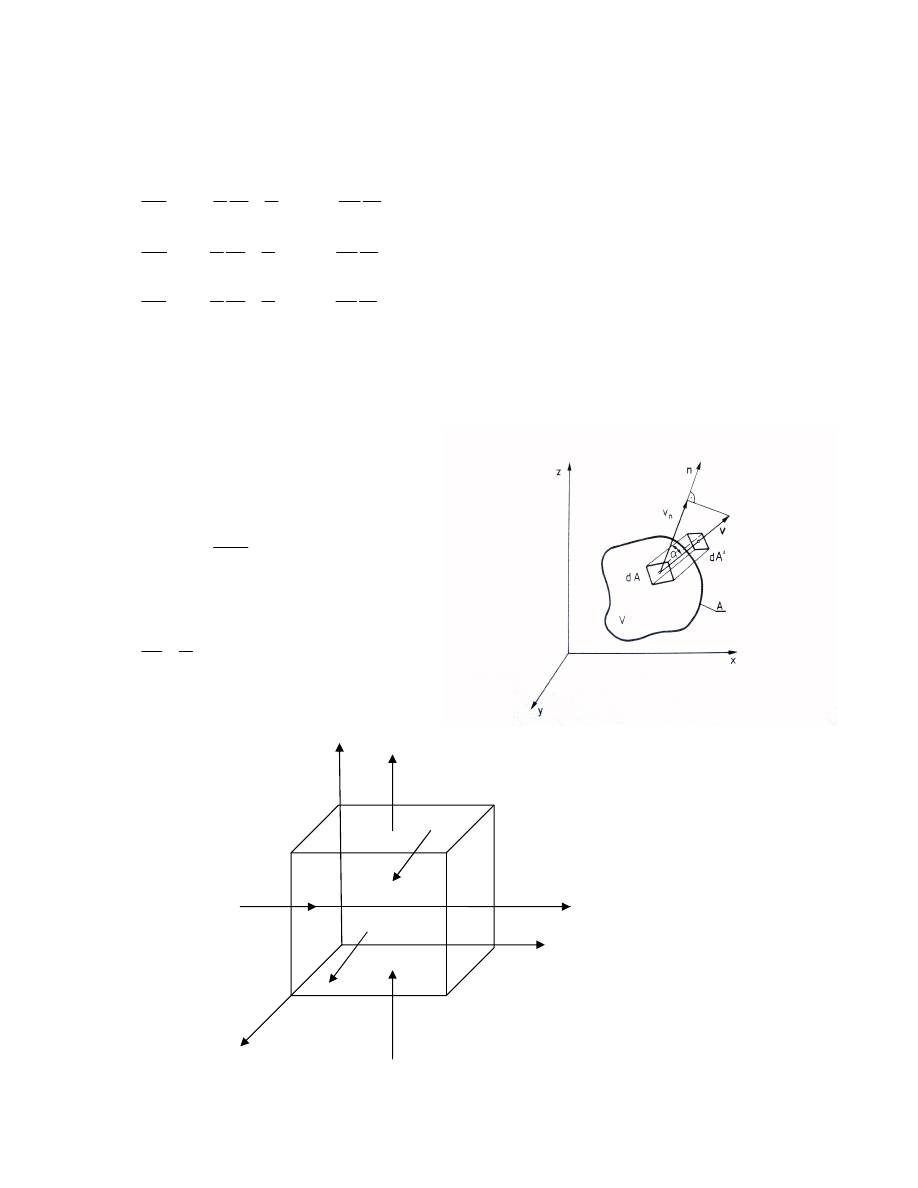
9. Tensor naprężenia elementu płynu
=
zz
zy
zx
yz
yy
yx
xz
xy
xx
ij
p
p
p
p
τ
τ
τ
τ
τ
τ
Pierwszy indeks oznacza kierunek normalny do ścianki, a drugi kierunek składowy siły
powierzchniowej; Siły powierzchniowe działają na każdą ściankę elementu płynu. Na każdej
ścianie występuje jedno naprężenie normalne (p
ii
) i dwa naprężenia styczne (
τ
ij
)
dy
y
p
p
dy
y
dy
y
dx
x
dx
x
p
p
dx
x
yy
yy
yz
yz
yx
yx
xy
xy
xx
xx
xz
xz
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
)
9
)
8
)
7
)
6
)
5
)
4
τ
τ
τ
τ
τ
τ
τ
τ
p
ab
:
a – oś prostopadła do płaszczyzny
b – kierunek działania
9
7
8
5
4
6
dz
z
p
p
zz
zz
∂
∂
+
dz
z
zx
zx
∂
∂
+
τ
τ
dz
z
zy
zy
∂
∂
+
τ
τ
xx
p
xz
τ
xy
τ
zx
τ
zy
τ
zz
p
yy
p
yz
τ
yx
τ
y
x
z
8
10. Równania Naviera-Stokesa
Równania opisują ruch płynu lepkiego i ściśliwego
(
)
(
)
(
)
(
)
(
)
(
)
v
div
z
v
z
p
Z
dt
v
v
div
y
v
y
p
Y
dt
v
v
div
x
v
x
p
X
dt
v
z
z
y
y
x
x
∂
∂
+
∇
+
∂
∂
−
=
∂
∂
∂
+
∇
+
∂
∂
−
=
∂
∂
∂
+
∇
+
∂
∂
−
=
∂
ρ
µ
ρ
µ
ρ
ρ
µ
ρ
µ
ρ
ρ
µ
ρ
µ
ρ
3
1
3
1
3
1
2
2
2
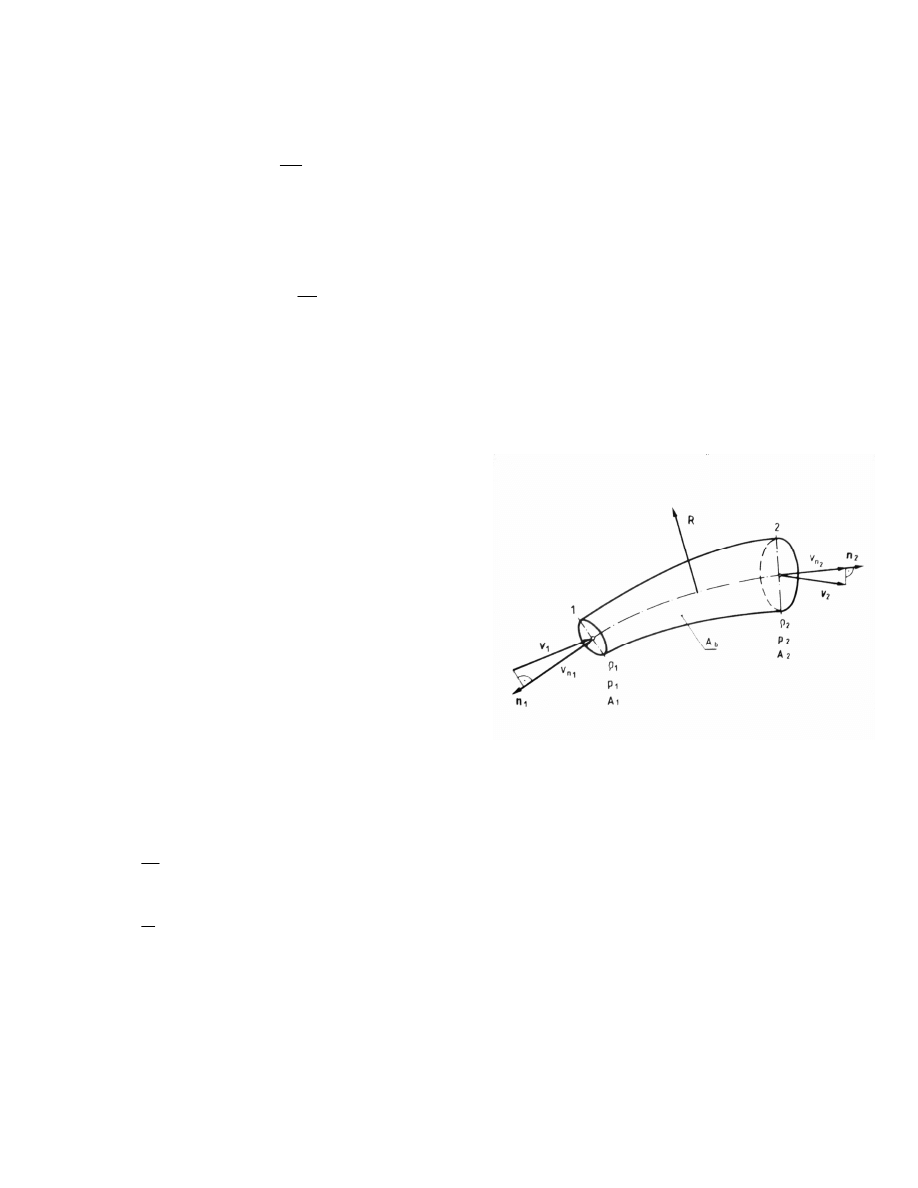
11. Równania ciągłości przepływu
Wyraża prawo zachowania masy. Rozpatrujemy objętość kontrolną V, ograniczoną
powierzchnią A. Dla objętości V możemy napisać, że strumienie masy przepływającej
(dopływ-odpływ) przez powierzchnię A muszą równać się akumulacji masy
∫∫
=
A
vdA
dt
m
ρ
&
masa zakumulowana w objętości V jest
równa:
dt
t
V
m
∂
∂
=
ρ
Dodając do siebie te dwie wielkości
otrzymujemy równania ciągłości
przepływu
0
1
=
+
∂
∂
∫∫
A
vdA
V
t
ρ
ρ
Interpretacja geometryczna:
B
C
G
H
E
F
D
A
x
y
z
m
x
+dm
m
z
+dm
m
z
m
x
m
y
m
y
+dm
9
12. Strumień objętości i masy płynu
Strumień objętości
s
m
3
jest iloczynem skalarnym prędkości v i odpowiednio
zorientowanego wektora elementu powierzchni dA [rysunek z zad. 11]
α
cos
∫∫
∫∫
∫∫
∫∫
=
=
=
=
A
A
n
A
A
vdA
dA
v
vndA
vdA
V&
Strumień masy płynu
s
kg
α
ρ
ρ
ρ
ρ
cos
∫∫
∫∫
∫∫
∫∫
=
=
=
=
A
A
n
A
A
vdA
dA
v
vndA
vdA
m
&
13. Strumień pędu i reakcja płynu przepływającego przez przewód krzywoliniowy
Wyznaczenie sił jakimi działa płyn będący w ruchu na ścianki przewodu lub na ciała
zanurzone w płynie jest możliwe z równań ruchu. Pomijając siły masowe, strumień pędu
płynu będącego w ruchu można:
dA
p
dA
vv
A
A
A
n
∫∫
∫∫
=
ρ
Oznaczając przez R przeciwną co do kierunku
działania siłę z jaką płyn działa na ściankę
Dla jednorodnych pól prędkości, ciśnień i gęstości
można zapisać:
2
2
2
1
1
1
2
1
.
)
(
A
p
n
A
p
n
v
v
m
R
−
−
−
= &
Dla jednowymiarowego przepływu ustalonego:
2
2
1
1
1
2
.
)
(
A
p
A
p
v
v
m
R
x
−
+
−
−
=
&
14. Równanie Bernoulliego
W kilku przypadkach możliwe jest rozwiązanie analityczne rownania ruchu Eulera i
uzyskanie związków miedzy prędkością przepływu i ciśnieniem. Dla ruchu ustalonego:
0
=
∂
∂
t
v
w przypadku płynu barotropowego, gęstość płynu zależy tylko od ciśnienia
gradP
gradp
=
ρ
1
Przez P oznaczono funkcję ciśnienia. Ponieważ pole sił masowych jest polem potencjalnym, o
potencjale U
gradU
F
m
=
∫∫
∫∫
∫∫
∫∫
−
−
−
=
1
2
1
2
2
1
2
2
2
1
1
1
2
2
2
1
1
1
A
A
A
A
n
n
dA
p
n
dA
p
n
dA
v
v
dA
v
v
R
ρ
ρ
10
Dla ruchu bezwirowego:
0
2
2
=
−
+
dU
dp
v
d
ρ
U podczas ruchu w ziemskim polu grawitacyjnym:
gz
U
−
=
Współrzędna z jest skierowana pionowo do góry. Całkując równanie Bernoulliego:
const
gz
p
v
=
+
+
ρ
2
2
Równanie dla płynów doskonałych ma formę równanie zachowania energii. Mnożąc pierwszy
człon przez masę m otrzymujemy energię kinetyczną płynu:
k
E
v
m
=
2
2
, a trzeci człon
p
E
mgz
=
- energię potencjalną
Suma tych energii stanowi energię mechaniczną płynu, która zmieni się w wyniku zmiany
ciśnienia.
Pomnożony drugi człon przez masę to praca sił ciśnienia, która zamyka bilans energii.
Inna postać równania Bernoulliego:
const
p
gz
p
v
c
=
=
+
+
ρ
ρ
2
2
po kolei: ciśnienie dynamiczne + ciśnienie statyczne + ciśnienie hydrostatyczne
15. Wypływ płynu do atmosfery przez dyszę, siły działające na kołnierz dyszy
[opracowane na podstawie przykładu 4.1 - Orzechowski]
Woda wypływa do atmosfery przewodem zwężającym się (dyszą). By wyznaczyć siłę
działającą na śruby łączące kołnierz dyszy z przewodem dolotowym o średnicy d
1
musimy
rozpatrzeć równanie Bernoulliego dla przekrojów [1] i [2] w postaci:
ρ
ρ
2
2
2
1
2
1
2
2
p
v
p
v
+
=
+
Znamy również powierzchnię przekroju
4
2
1
1
d
A
π
=
. Korzystając z równania ciągłości:
2
2
1
1
v
A
v
A
=
i ze zmierzonego ciśnienia w przekroju [1] i [2]
(
)
2
1
p
p
−
jesteśmy w stanie
wyliczyć prędkość v
2
.
Siła działająca na śruby równa jest reakcji R wywieranej przez wodę na dyszę:
(
)
2
2
1
1
1
2
1
1
A
p
A
p
v
v
A
v
R
−
+
−
−
=
ρ
(Jeśli znane jest tylko nadciśnienie p
1
to p
2
=0)
A
1
A
2
v
2
v
1
1
2
d
1
p
1
p
2
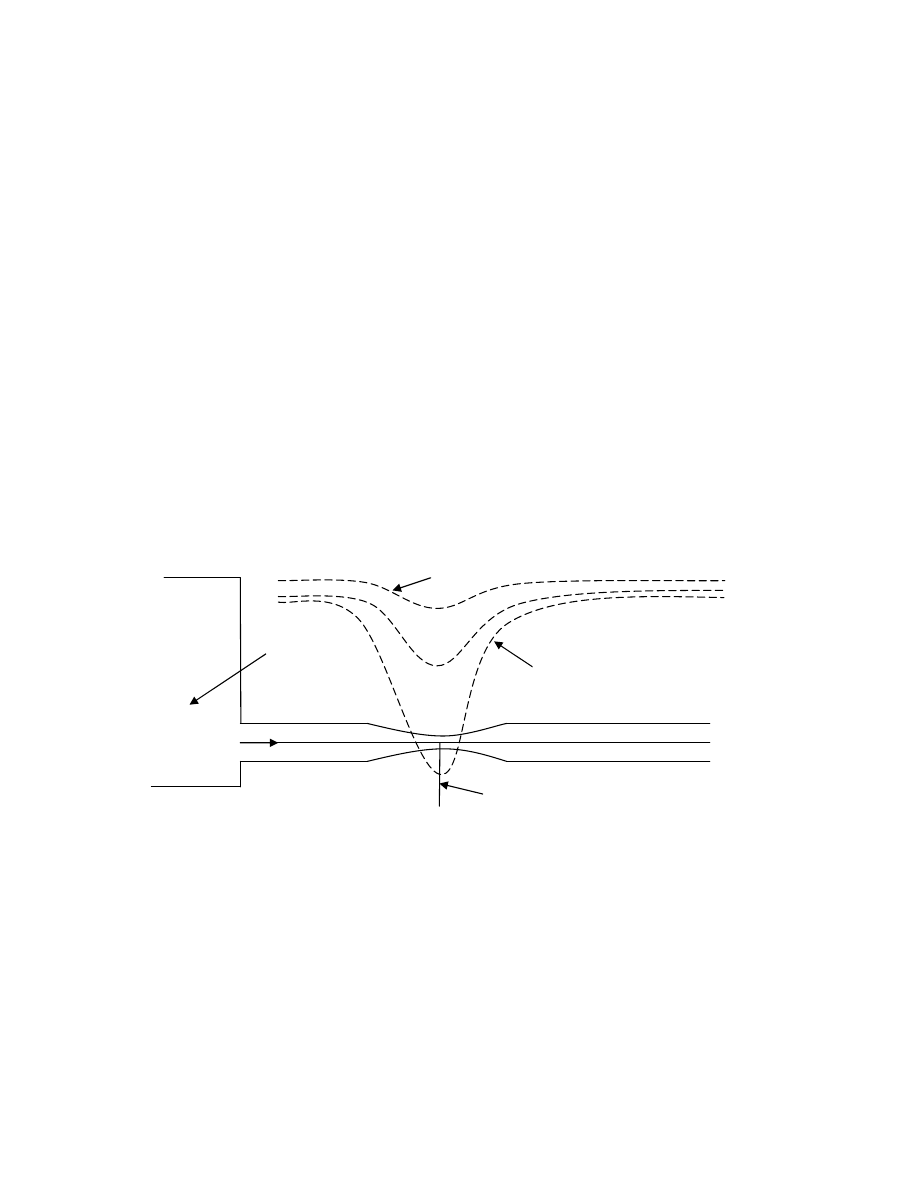
11
16. Zaburzenia przepływu przy opływaniu przegród
W przepływach rzeczywistych ciecze charakteryzują się lepkością co prowadzi do zaburzeń
przepływu. W wyniku działania sił lepkości warstwy cieczy przylegające do przeszkody
posiadają mniejszą prędkość niż to wynika z przepływów cieczy idealnej. W rezultacie
tworzy się warstwa o określonej grubości która zazwyczaj zwiększa swoją grubość wraz z
przebytą drogą przez płyn. Ponieważ jednak przez przeszkody zewnętrzne warstwy płynu
przyśpieszają, grubość warstwy o prędkości niższej od średniej nie zwiększa się. Za
przegrodą następuje zwolnienie prędkości płynu.
17. Kawitacja, przyczyny powstawania, skutki eksploatacyjne
Kawitacja jest zjawiskiem polegającym na tworzeniu się w cieczy pęcherzy gazu a następnie
ich znikania. Zjawisko to powstaje tam gdzie ciśnienie cieczy spadnie do poziomu ciśnienia
parowania. W rezultacie powstają pęcherze par cieczy, które po przejściu do stref o wyższym
ciśnieniu znikają. W rezultacie powstają silne efekty dynamiczne prowadzące do obniżenia
sprawności systemu tłoczenia oraz do szybkiego zużywania się elementów układów
hydraulicznych przewodów tłoczących. (W momencie zaniku pęcherzy powstają lokalne
skoki ciśnienia sięgające wartości 800 MPa. W rezultacie występuje w tych miejscach szybkie
zużycie ścian, kanałów, łopatek turbin, zaworów itd.)
18. Podobieństwo zjawisk przepływowych
Przepływy są podobne gdy spełniają podobieństwa:
- geometryczne (definiowane współczynnikiem skali podobieństwa – określa on stosunek
wymiarów modelu do wymiarów obiektu rzeczywistego)
- kinematyczne (odnosi się do pól prędkości modelu i obiektu tzn. linie płynięcia powinny
przebiegać identycznie, przy zachowaniu współczynnika skali)
- dynamiczne (spełniona analiza wymiarowa i bezwymiarowa)
Duże znaczenie praktyczne ma analiza bezwymiarowa – głównie twierdzenie o
podobieństwie zjawisk – jeżeli dwa porównywalne zjawiska są opisywane w postaci
bezwymiarowej identycznym układem równań i warunków brzegowych to zjawiska te są
podobne.
woda
T=20
o
C
mała prędkość
duża prędkość
krytyczne podciśnienie
V
o
prędko
12
W przypadku przepływów model i obiekt rzeczywisty musza spełniać ten sam układ
równań Naviera-Stokesa
Parametry bezwymiarowy:
0
0
0
ˆ
,
ˆ
,
ˆ
L
z
z
L
y
y
L
x
x
=
=
=
0
0
0
ˆ
,
ˆ
,
ˆ
v
v
v
v
v
v
v
v
v
z
z
y
y
x
x
=
=
=
0
0
0
ˆ
,
ˆ
,
ˆ
ρ
ρ
ρ
=
=
=
p
p
p
t
t
t
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
⋅
⋅
−
⋅
=
2
2
2
2
2
2
0
0
2
0
0
0
2
0
0
0
0
0
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
1
ˆ
ˆ
z
v
y
v
x
v
v
L
x
p
v
p
g
X
v
gL
t
d
v
d
t
v
L
x
x
x
x
ν
ρ
ρ
Gdzie wyrażenia w nawiasach są liczbami podobieństwa
0
0
0
L
t
v
St
=
- liczba Strouhala (odgrywa role w przepływach nieustalonych czyli takich z
przyspieszeniami lokalnymi)
0
2
0
gL
v
Fr
=
- liczba Froude’a (określa stosunek sił bezwładności do sił masowych decyduje o
zjawiskach na powierzchni cieczy)
2
0
0
v
p
Eu
ρ
=
- liczba Eulera (stosunek ciśnienia statycznego do dynamicznego odgrywa rolę
przy dużych prędkościami przepływu)
ν
0
0
Re
L
v
=
- liczba Reynoldsa (wyraża stosunek sił bezwładności do sił lepkości (Ważna w
przepływach lepkich)
19. Przepływ laminarny w przewodzie płaskim
Charakteryzuje się znaczną przewagą sił lepkości nad siłami bezwładności. Poszczególne
warstwy przemieszczają się równolegle względem siebie.
Przepływ między nieruchomymi ścianami płaskimi jest wywołany różnicą ciśnień na wejściu
i wyjściu do kanału.
L
p
x
p
str
−
=
∂
∂
L – droga przebyta przez płyn
Cechy przepływu:
0
=
y
v
- brak przepływu w poprzek kanału
0
=
z
v
- linie prądu równoległe do osi x
v
v
x
= - wypadkowa prędkość
0
=
∂
∂
t
v
x
- przepływ jest ustalony
0
=
∂
∂
x
v
x
- prędkość v
x
nie zależy od kierunku x

13
Siły masowe pomija się.
Równanie Naviera-Stokesa przyjmuje postać
νρ
µ
µ
=
−
=
,
2
2
L
p
dz
v
d
str
- współczynnik lepkości
dynamicznej
Po całkowaniu otrzymujemy:
)
(
2
z
s
z
L
p
v
str
−
=
µ
- równanie płaskiego przepływu laminarnego
2
max
8
s
L
p
v
str
µ
=
2
max
12
3
2
s
L
p
v
v
str
µ
=
=
20. Przepływ laminarny w przewodzie o przekroju kołowym
W przypadku przepływu laminarnego brak jest ruchu płynu w kierunku prostopadłym do lini
płynięcia. Nie występuje spadek ciśnienia dynamicznego w kierunku prostopadłym do linii
płynięcia i suma ciśnienia strat i ciśnienia hydrostatycznego jest stała.
Gradient ciśnienia
(
)
const
gz
p
ds
d
=
+
−
ρ
w przekroju przewodu. Naprężenie styczne równe
jest 0 w osi przewodu, a na ściance osiąga maksimum:
dy
dv
µ
τ
=
. Ze względu na przeciwny
zwrot współrzędnych r i y:
dr
dv
dy
dv
−
=
, rozkład prędkości przyjmuje postać:
(
)
(
)
+
−
−
=
⇒
+
−
−
=
gz
p
ds
d
r
r
v
gz
p
ds
d
r
dr
dv
ρ
µ
ρ
µ
4
2
2
2
0
Strumień objętości wynosi:
(
)
+
−
=
gz
p
ds
d
r
V
ρ
µ
π
8
4
0
&
Średnia prędkość wynosi:
(
)
+
−
=
gz
p
ds
d
r
v
ρ
µ
8
2
0
Strata ciśnienia:
(
)
2
0
2
0
8
8
r
g
L
v
p
r
v
gz
p
ds
d
str
ρ
µ
µ
ρ
=
⇒
−
=
+

14
21. Spływ cieczy po ścianie pionowej
W warunkach jednostajnego laminarnego spływu cieczy po ścianie pionowej prędkości w
kierunku prostopadłym do ściany i w kierunku szerokości są równe zero. Nie występują
również zmiany ciśnienia w żadnym kierunku. W rezultacie pozostaje jedynie równanie
Naviera – Stokesa dla kierunku z w postaci:
3
2
0
2
1
2
max
2
1
2
2
2
3
3
1
2
2
0
0
0
0
:
2
0
x
x
z
x
x
z
x
z
z
x
z
z
z
g
v
V
g
dx
v
v
x
x
g
v
g
C
C
dx
dv
v
v
x
v
x
warunki
C
x
C
x
g
v
dx
v
d
Z
x
δ
µ
ρ
δ
δ
µ
ρ
δ
δ
µ
ρ
δ
µ
ρ
δ
µ
ρ
ρ
µ
δ
=
=
=
=
−
=
=
∧
=
⇒
=
⇒
=
⇒
=
=
⇒
=
+
+
−
=
⋅
+
=
∫
&
x
δ
- grubość spływającej warstwy cieczy
Z przeprowadzonych badań wynika, że otrzymane zależności są słuszne dla niewielkich liczb
Reynoldsa, do zakresu w którym następuje powstawanie fal na powierzchni swobodnej
cieczy.
22. Podstawowe parametry przepływu turbulentnego
Jego cechą jest przestrzenny charakter, w którym elementy płynu poruszają się w sposób
nieustalony . Zaburzenia są wynikiem sił tarcia na powierzchnię ścian przewodu. Utrata
stateczności rozpoczyna się od brzegu strugi i rozprzestrzenia na całą objętość.
- parametry przepływu:
′
+
=
′
+
=
′
+
=
z
z
z
y
y
y
x
x
x
v
v
v
v
v
v
v
v
v
x
v
- uśredniona składowa prędkości,
x
v′
- składowa
prędkości pulsacji dla kierunku x
- średnia składowa prędkości:
dt
v
t
t
v
t
t
x
x
∫
−
=
2
1
1
2
1
, gdzie
1
2
t
t
− to przedział czasu
- średnia składowa pulsacji:
0
1
2
1
1
2
=
′
−
=
′
∫
dt
v
t
t
v
t
t
x
x
(składowe są zawsze dodatnie)
- turbulencję przepływu można scharakteryzować za pomocą parametrów bezwymiarowych
- intensywność turbulencji przepływu
ε
(ogólnie)
v
v
2
′
=
ε
g
Z
const
=
=
ρ
µ
δ
,
,
15
23. Rozkład prędkości w przepływie turbulentnym
Trudne do określenia na drodze teoretycznej, przy dużych prędkościach zbliżony do rozkładu
prostokątnego charakterystycznego dla przepływu płynów doskonałych (nielepkich).
Rozkład prędkości opisujemy wzorem Prandtla
n
R
r
v
v
1
max
1
−
=
n – zależy od Re i wynosi 6-10 dla przewodów gładkich i 4-5 dla chropowatych.
Rozkład prędkości w przekroju strugi
( )
2
2
3
max
1
−
=
b
z
v
v
x
x
gdzie:
( )
max
x
v
- prędkość maksymalna w danym przekroju strugi
z – rzędna
b – grubość warstwy granicznej
24. Laminarna warstwa przyścienna - opory przepływu
Laminarną warstwę przyścienną można opisać równaniami Naviera–Stokesa.
∂
∂
+
∂
∂
+
∂
∂
−
=
∂
∂
+
∂
∂
∂
∂
+
∂
∂
+
∂
∂
−
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
2
2
2
2
2
2
2
2
1
1
0
z
v
x
v
z
p
z
v
v
x
v
v
z
v
x
v
x
p
z
v
v
x
v
v
z
v
x
v
z
z
x
z
z
x
x
x
x
z
x
x
z
x
ν
ρ
ν
ρ
Z równań tych otrzymuje się układ równań Prandtla dla laminarnej warstwy przyściennej
0
1
0
2
2
=
∂
∂
∂
∂
+
∂
∂
−
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
z
p
z
v
x
p
z
v
v
x
v
v
z
v
x
v
x
x
z
x
x
z
x
ν
ρ
1,0
0,8
0,6
0,4
0,2
0
1,0 0,8 0,6 0,4 0,3 0,2 0
max
v
v
R
r
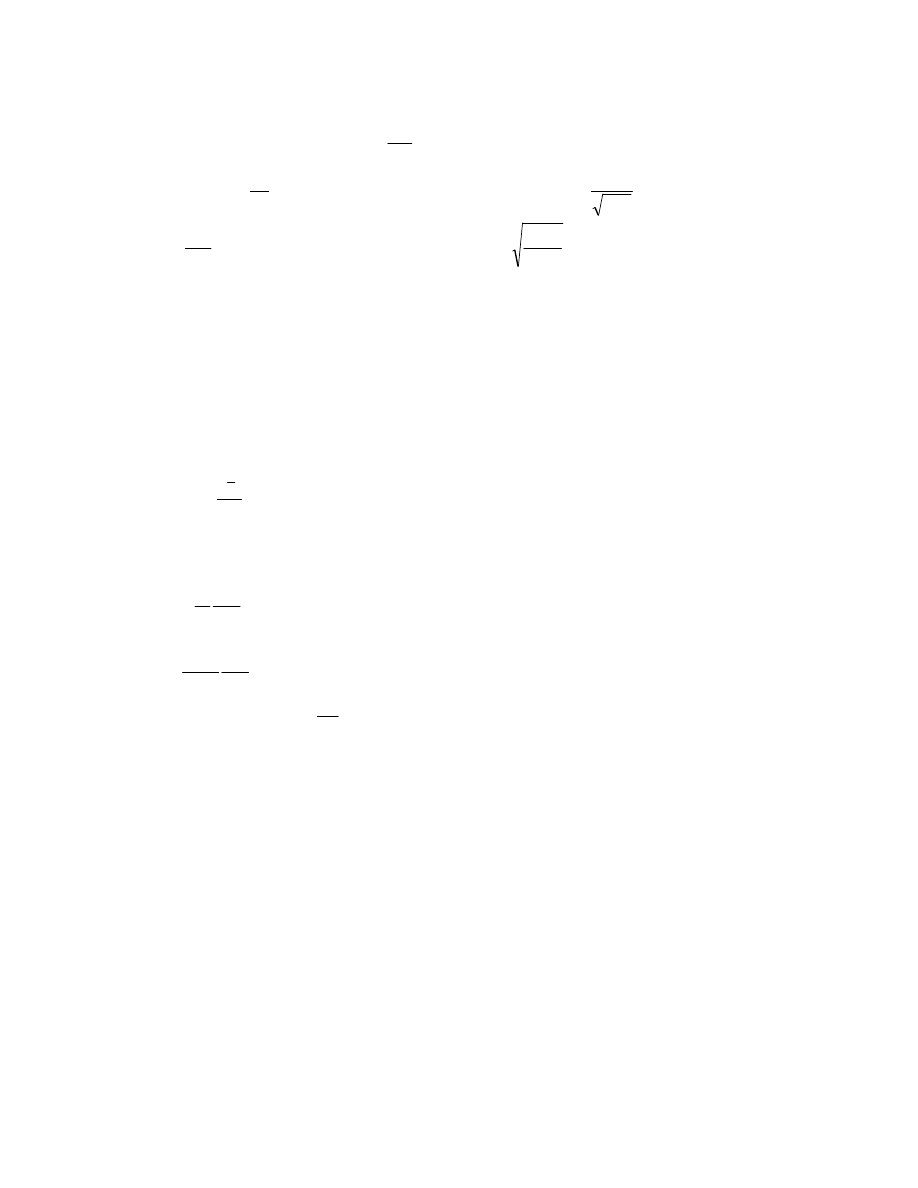
16
Rozwiązanie tego układu równań umożliwia znalezienie rozkładu prędkości na powierzchni, a
stąd naprężenie stycznego:
0
=
∂
∂
=
z
x
lam
z
v
µ
τ
, znajomość
lam
τ
umożliwia obliczenie oporu
przepływu. Dla
0
=
∂
∂
x
p
grubość warstwy laminarnej wynosi:
x
x
Re
5
=
δ
, gdzie:
ν
x
v
x
∞
=
Re
zaś naprężenie na powierzchni:
x
v
lam
3
332
,
0
∞
=
ρµ
τ
25. Turbulentna warstwa przyścienna - opory przepływu
Przy samej powierzchni występuje cienka podwarstwa laminarna o grubości δ
lam
. Powyżej
podwarstwy laminarnej rozkład prędkości ma charakter logarytmiczny. Naprężenie styczne w
turbulentnej warstwie przyściennej są sumą naprężeń laminarnych i naprężeń turbulentnych.
turb
lam
τ
τ
τ
+
=
, gdzie
lam
τ
- składowa laminarna naprężenia stycznego,
turb
τ
- składowa
turbulentna naprężenia stycznego
W podwarstwie naprężenie styczne jest w przybliżeniu stałe, w rezultacie rozkład prędkości w
tej podwarstwie jest w przybliżeniu liniowy.
W turbulentnej części warstwy (rdzeniu turbulentnym), naprężenie wynosi:
2
2
∂
∂
=
z
v
L
x
turb
ρ
τ
, gdzie: L - droga mieszania
26. Współczynnik tarcia w warstwie przyściennej, wpływ chropowatości przewodu
Straty ciśnienia wskutek tarcia obliczane są ze wzoru Darcy-Weisbacha
2
2
v
D
L
p
str
ρ
λ
=
, gdzie
λ
- współczynnik tarcia wewnętrznego płynu w przewodzie
prostoliniowym o średnicy D i długości L, inaczej:
2
Re
64
2
v
D
L
p
str
ρ
=
Współczynnik tarcia:
Re
64
=
λ
Wpływ chropowatości na wartość współczynnika λ, a więc i na opory tarcia jest złożony.
Grubość podwarstwy laminarnej decyduje o tym, czy przewód może być uznany za
hydraulicznie gładki
a)
lam
k
δ
<
(czyli chropowatość bezwzględna k mniejsza od grubości podwarstwowej warstwy
laminarnej)
–
brak
wpływu
chropowatości
na
współczynnik
tarcia.
b)
lam
k
δ
>
(zakres przejściowy) – wpływ chropowatości zmienia się wraz ze zmianą liczby
Reynoldsa
c)
lam
k
δ
>>
(chropowatość bezwzględna dużo większa niż grubość warstwy laminarnej) – w
pełni rozwinięty wpływ chropowatości – współczynnik tarcia
λ
nie zależy od Re.
Chropowatość bezwzględna to średnia wysokość nierównomierności ścian rury.

17
27. Straty ciśnienia podczas tarcia
Straty ciśnienia są wywołane tarciem wewnętrznym płynu w obszarze warstwy przyściennej.
Straty te nazywane też są stratami liniowymi.
Straty ciśnienia
2
2
v
D
L
p
t
str
ρ
λ
=
g
v
D
L
z
t
str
2
2
λ
=
Wzór ten umożliwia obliczenie strat ciśnienia wskutek tarcia, dotyczy przepływu laminarnego
i turbulentnego, ale współczynnik λ w obu przypadkach przyjmuje inną wartość
28. Straty ciśnienia w wyniku oporów miejscowych
Opory miejscowe są spowodowane zmianą wartości i kierunku prędkości. Zmiany te
zachodzą w różnych miejscach przewodu i są spowodowane takimi przeszkodami, jak kolana,
przewężenia, rozszerzenia, rozgałęzienia.
2
2
v
p
m
str
ρ
ξ
=
Przy przepływie cieczy stratę często wyraża się w metrach słupa danej cieczy, a mianowicie:
g
v
z
m
str
2
2
ξ
=
Współczynniki strat miejscowych ξ są określone na drodze doświadczalnej.
opracowanie na podst. wykładów: kszyh
Wyszukiwarka
Podobne podstrony:
mechanika plynow opracowanie zagadnien
mechanika plynow opracowane zagadnienia (2), Sprawka
mechana plynow opracowane zagadnienia kolo1, PG inżynierka, Semestr 3, Mechanika płynów, wykład
Mechanika płynów opracowane zagadnienia, Inżynieria Środowiska-Szczecin, Mechanika płynów, Wykłady+k
mechanika płynów 46-49, Mechanika płynów 1, Opracowania
Mechanika płynów opracowanie
mechanika plynow opracowanie
mechana plynow opracowane zagadnienia, OiO sem. III, mechanika płynów
Mechanika plynow opracowanie
Mechanika plynow opracowanie wersja zmniejszona
mechanika plynow opracowanie zagadnien
mechanika plynow opracowanie
Opracowane pytania na mechanikę płynów
opracowane pytania, Mechanika Płynów - laborki
OPRACOWANE ZAGADNIENIE NR 3, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Se
więcej podobnych podstron