MACIERZ SZTYWNOŚCI PŁASKIEGO ELEMENTU PROSTOKĄTNEGO

KROK 1. OKREŚLENIE TYPU ELEMENTU.

Zbudujemy macierz sztywności płaskiego elementu prostokątnego pokazanego na rys.1

Element ten o wymiarach podstawy 2a i wysokości 2b posiada 4 wierzchołki oznaczone jako: 1,2,3,4

Nieznane przemieszczenia wierzchołków są dane jako:

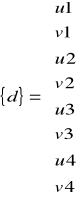
(1)

u₁ - v₄ są to parametry geometryczne, poziome i pionowe przemieszczenia węzłów.

KROK 2. OPIS POLA PRZEMIESZCZEŃ.

Parametry geometryczne (1) zostały zebrane w dwie macierze z elementami uszeregowanymi w kolejności odpowiadającej osiom x,y dla poszczególnych węzłów.

Opis pola przemieszczeń będzie wyrażony za pomocą składowych: u(x,y) v(x,y)

Funkcje przemieszczeń u i v elementu muszą być liniowe, ponieważ wzdłuż każdej krawędzi istnieją tylko dwa wierzchołki.

u(x, y) = a₁ + a₂x + a₃y + a₄xy (2)

v(x, y) = a₅ + a₆x + a₇y + a₈xy

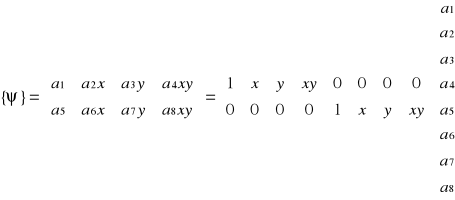
Poszukiwana macierz sztywności ma wymiary 8x8 . Składowe pola przemieszczeń opisane są wielomianami liniowymi dwóch zmiennych . Z każdą ze składowych związane są 4 parametry węzłowe.

Niewiadome stałe a₁, a₂ do a₆ wyrażamy przez geometryczne parametry węzłowe, rozwiązując dwa układy równań:

u₁ = a₁ + a₂x₁ + a₃y₁ + a₄x₁y₁

u₂ = a₁ + a₂x₂ + a₃y₂ + a₄x₂y₂ (3)

u₃ = a₁ + a₂x₃ + a₃y₃ + a₄x₃y₃

u₄ = a₁ + a₂x₄ + a₃y₄ + a₄x₄y₄

v₁ = a₁ + a₂x₁ + a₃y₁ + a₄x₁y₁

v₂ = a₁ + a₂x₂ + a₃y₂ + a₄x₂y₂

v₃ = a₁ + a₂x₃ + a₃y₃ + a₄x₃y₃ (4)

v₄ = a₁ + a₂x₄ + a₃y₄ + a₄x₄y₄

gdzie:

u₁ = u(x₁,y₁), u₂ = u(x₂,y₂), itd.

Po rozwiązaniu układów równań (3) i (4) i wstawieniu do równania (2) otrzymujemy:

u(x, y) =
[(b - x)(h - y)u₁ + (b + x)(h - y)u₂+ (b + x)(h + y)u₃ + (b - x)(h + y)u₄] (5)

ν(x, y) =
[(b - x)(h - y)v₁ + (b + x)(h - y)ν₂ + (b + x)(h + y)u₃ + (b - x)(h + y) ν₄]

Dostrzegamy, że wyrażenia w (5) są przedstawione za pomocą funkcji kształtu oraz przemieszczeń wierzchołków:

{ψ} = [N]{d} (6)

gdzie:

d - wektor przemieszczenia wierzchołków

N - macierze funkcji kształtu :

N₁ =
N₂ =

(7)

N₃ =
N₄ =

Przykładowo: N₁ = 1 dla wierzchołka 1 i N₁ = 0 dla pozostałych wierzchołków.

W formie rozszerzonej, równanie (6) ma postać:

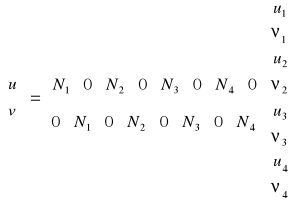
(8)

KROK 3. OPIS POLA ODKSZTAŁCEŃ.

Odkształcenia możemy wyrazić w nast. sposób:

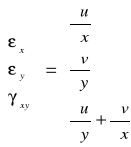
(9)

Po podstawieniu równania (8) i do równania (9) oraz po wyliczeniu pochodnych

u i v, możemy wyrazić odkształcenia w nast. sposób:

{ε} = [B]{d} (10)

gdzie:

B - macierz przemieszczeń

d - wektor przemieszczenia wierzchołków

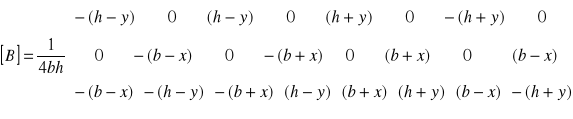
(11)

Z równań (9) i (10) wynika, że ε_x jest funkcją y ; ε _y jest funkcją x, a γ_xy jest funkcją

x i y.

KROK4. OPIS POLA NAPRĘŻEŃ.

Pole naprężeń opisujemy:

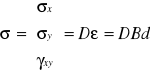
(12)

gdzie:

D - macierz sztywności materiału

KROK5. RÓWNANIE MACIERZY SZTYWNOŚCI ELEMENTU.

Równanie to ma postać:

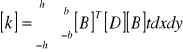
(13)

Poszukiwana macierz sztywności [k] dla elementu prostokątnego jest macierzą o wymiarach 8x8.

Uwzględnienie obciążeń międzywęzłowych , objętościowych i powierzchniowych wygląda następująco:

(14)

gdzie:

{X} - siły od obciążeń objętościowych

{T} - siły od obciążeń powierzchniowych

{P} - siły od obciążeń skupionych

[N] - prostokątna macierz funkcji kształtu z wzoru (8)

MACIERZ SZTYWNOŚCI DLA ELEMENTU IZOPARAMETRYCZNEGO.

Koncepcja elementu izoparametrycznego (elementu o konturach zakrzywionych) powstała na tle trudności występujących przy analizowaniu obszarów z brzegami zakrzywionymi. Uzyskanie dokładnych wyników przy użyciu elementów ograniczonych liniami prostymi wymagałoby użycia dużej liczby takich elementów. Główna trudność jaka występuje przy analizie elementów izoparametrycznych dotyczy opisu pola przemieszczeń i uzyskania macierzy sztywności. Trudności te zostały przezwyciężone dzięki możliwości odwzorowania skomplikowanego kształtu geometrycznego przez prostszy. Można zatem przeprowadzać wszystkie operacje na elemencie prostszym - macierzystym i przenosić wyniki na element izoparametryczny. Opisu geometrii i przemieszczeń elementu izoparametrycznego dokonujemy za pomocą tych samych funkcji i takiej samej liczby parametrów jak dla elementu prostego.

Rozważymy element tarczowy , prostokątny o 4 węzłach ( Rys.1 ). Jest to element 8 parametrowy. Parametrami są przemieszczenia węzłów.

KROK1. WYZNACZENIE POLA PRZEMIESZCZEŃ I FUNKCJI KSZTAŁTU.

Pole przemieszczeń opisane jest równaniem macierzowym:

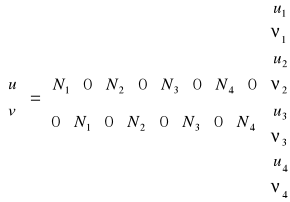
(1)

Występujące we wzorze (1) funkcje kształtu mają jak wcześnie postać:

N₁ =
N₂ =

(2)

N₃ =
N₄ =

Funkcje te dla kwadratu pokazanego na Rys.1 wyrażają się następująco:

N₁ =
N₂ =

(3)

N₃ =
N₄ =

Potraktujemy ten kwadrat jako element macierzysty i powiążemy jego geometrie z geometrią dowolnego czworokąta pokazanego na Rys.2

Boki czworokąta są liniami prostymi więc współrzędne x, y będą zależały liniowo od współrzędnych s, t

Współrzędne x, y określamy wzorami:

x = a₁ + a₂s + a₃t + a₄st (4)

y = a₅ + a₆s + a₇t + a₈st

Chcąc otrzymać niewiadome stałe a₁, a₂ do a₈ postępujemy jak w przypadku elementu prostokątnego i otrzymujemy:

x =
[(1 - s)(1 - t)x₁ + (1 + s)(1 - t)x₂+ (1 + s)(1 + t)x₃ + (1 - s)(1 + t)x₄] (5)

y =
[(1 - s)(1 - t)y₁ + (1 + s)(1 - t)y₂ + (1 + s)(1 + t)y₃ + (1 - s)(1 + t) y₄]

lub zapisując w formie macierzy:

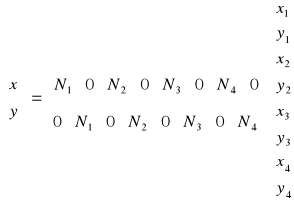
(6)

Z powyższego widać, że funkcje N_i (3) przekształcają kwadrat (Rys. 1) w układzie s, t w dowolny czworokąt opisany współrzędnymi x₁, y₁,..... w układzie x, y .

Porównanie (1) oraz (6) wykazuje, że pole przemieszczeń i geometria opisane są tymi samymi funkcjami i taką samą liczbą parametrów.

Zauważyć można również, że funkcje kształtu w równaniu (3) są po raz kolejny takie, że N₁ do N₄ jest równe 1 na danym wierzchołku oraz równe zeru na wszystkich innych wierzchołkach.

Dla przykładu, N₁ przedstawia geometryczny kształt dla x₁ = 1, y₁ = 1 a x₂, y₂, x₃, y₃, x₄, oraz y₄ wszystkie równe zero.

(i= 1,2....,n)

KROK 2: Ustalenie funkcji przemieszczenia

Funkcje przemieszczania w elemencie są podobnie definiowane przez te same funkcje kształtu jakie używane są do określania kształtu elementu, to jest:

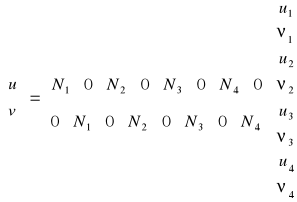
(7)

gdzie u i v są przemieszczeniami równoległymi do głównych współrzędnych x i y, a funkcje kształtu są określone przez równania (3).

Porównując równania (1) i (7), widzimy podobieństwa pomiędzy prostokątnym elementem z bokami o długościach 2b i 2h (rys. 1) oraz kwadratowy element z bokami o długości 2. Jeżeli b = l i h = l, dwa równania funkcji kształtu czyli równania (2) i (3), będą identyczne.

KROK 3: Zdefiniować związki odkształcenia/przemieszczenia oraz naprężenia/odkształcenia.

Aby sformułować element macierzy [B] przedstawiono funkcje kształtu we współrzędnych izoparametrycznych s i t, ponieważ wyrażenie funkcji kształtu we współrzędnych x i y było by niemożliwe.

Aby skonstruować element macierzy sztywności, musimy ustalić odkształcenia, które są zdefiniowane jako przemieszczenia opisane przez współrzędne x i y. Przemieszczenia powinny być opisane jako funkcje współrzędnych s i t, jak podano w równaniu (7), razem z funkcjami kształtu określonymi przez równania (3). Możemy wcześniej określić(
f/
x) i (
f/
y), gdzie, f jest funkcją reprezentującą funkcje przemieszczeń u lub v. Jakkolwiek u i v są teraz wyrażane w jednostkach s i t. W tym celu musimy skorzystać z reguły zbioru uporządkowanego liniowo ponieważ nie będzie możliwe bezpośrednie wyrażenie s i t jako funkcji x i y. Funkcję f można wyrazić w następujący sposób:

(8)

W równaniach (8), dane są (
f/
s), (
f/
t), (
x/
s), (
y/
s) (
x/
t), i (
y/
t) uzyskane z równań (7) i (4). Natomiast poszukujemy (
f/
x) i (
f/
y). Odkształcenia mogą być wyznaczone jako ε_x = (
u/
x). W tym celu, rozwiązujemy równania (8) dla (
f/
x) i (
f/
y) korzystając z reguły Cramer-a która dotyczy oszacowania wartości:

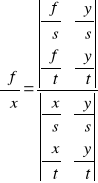
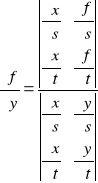
(9)

gdzie wyznacznikiem w mianowniku jest wyznacznik Jacobian-a macierzy J. Hence, macierz Jacobian-a jest podana jako:

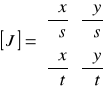
(10)

Możemy teraz wyrazić odkształcenia elementu jako:

ε = B d (11)

gdzie B musi być teraz wyrażone jako funkcja s i t. Możemy pokazać, że zachodzi związek pomiędzy odkształceniami a przemieszczeniami podanymi w macierzy:

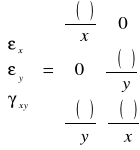
(12)

gdzie macierz prostokątna po prawej stronie równania (12) jest operatorem macierzy to jest,
( )/
x i
( )/
y przedstawiają pochodne cząstkowe zmiennej, którą można umieścić w środku nawiasów. Używając równania (9), mamy:

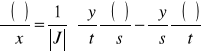
(13)

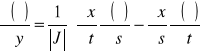
gdzie
jest wyznacznikiem J. Używając równania (13) w równaniu (12) otrzymujemy odkształcenia wyrażone we współrzędnych (s-t) jako:

=
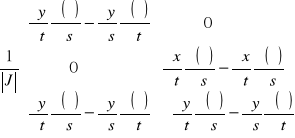
(14)

Używając równania (7), możemy przedstawić równanie (14) jako funkcje kształtu i ogólne współrzędne formy macierzy:

(15)

gdzie D jest operatorem macierzy podanej jako:

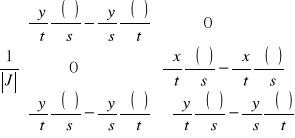
(16)

N jest funkcją macierzy kształtu 2 x 8, podanej jako pierwsza macierz po prawej stronie równania (7) a d jest kolumną macierzy po prawej stronie równania (7).

Definiując B jako:

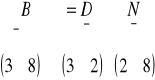
(17)

mamy B wyrażone jako funkcję s i t

KROK4. Wyprowadzanie równania macierzy sztywności.

Chcemy teraz przedstawić macierz sztywności we współrzędnych s i t. Dla stałej grubości elementu mamy:

[k] =
[B]^T[D][B]tdxdy (18)

B jest funkcją s i t, więc musimy [k] całkować po s i t. Po raz kolejny, aby przekształcić zmienne i obszar z x i y na s i t, musimy przeprowadzić standardową procedurę, która zawiera wyznacznik J. Ten główny typ przekształceń podano w następujący sposób:

(19)

gdzie należy podstawić |J| w prawej stronie równania (19), co wynika z twierdzenia

o rachunku całkowym. Podstawiając równanie (19) do równania (18), otrzymujemy:

(20)

Wyznacznik |J| jest wielomianem we współrzędnych s i t. Jakkolwiek używając równania (10) dla [J] i równania (3) dla x i y, możemy określić |J| jako:

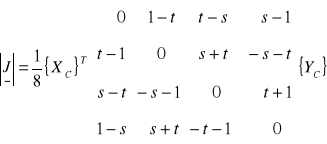
(21)

gdzie:

(22)

oraz:

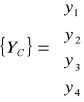
(23)

Zauważmy, że |J| jest funkcją s i t i znanymi głównymi współrzędnymi x₁, x₂, …, y₄

Dokładniej można wyrazić B przez zastąpienie równania (16) dla D' i równań (5) dla funkcji kształtu w równaniu (17). Otrzymujemy wtedy mnożenie macierzy przez odwrotność wyznacznika J:

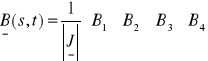
(24)

gdzie podmatryce B są podane przez:

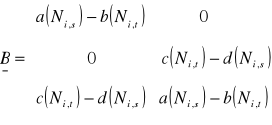
(25)

gdzie i jest równy 1, 2, 3, i 4 wiec otrzymujemy:

(26)

Używając funkcji kształtu zdefiniowanych przez równania (5) otrzymujemy:

(27)

Od tego momentu, B jest funkcją s i t w liczniku i mianowniku (przez |J| dane przez równanie (21)) o znanych głównych współrzędnych x₁ do y₄. Również |J| i B są takie, jak wynik skomplikowanych wyrażeń w równaniu (20), więc całkując można wyznaczyć element macierzy sztywności. Element bryły macierzy będzie teraz określany jako:

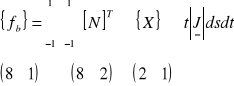
(28)

a powierzchnia macierzy, załóżmy, wzdłuż krawędzi t=1 (zobacz rys. 2) z całkowitą długością L, jest wyrażona:

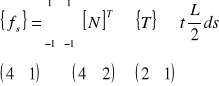
(29)

lub:

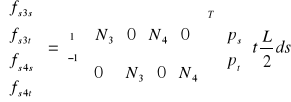
(30)

Od tej chwili N₁ = 0 i N₂=0 wzdłuż krawędzi t=1, również żadne siły węzłowe nie istnieją w węzłach 1 i 2.

Rys.1

Rys.2

---