TRANSCOMP 2007 |
MODELE INTERFERENCYJNE W BEZPRZEWODOWYCH SIECIACH TYPU AD-HOC
Stefan JACKOWSKI, Bartłomiej KOCOT
Wojskowa Akademia Techniczna, Wydział Elektroniki
ul. Kaliskiego 2, 00-903 Warszawa, tel.: 022 683 70 98,
e-mail: stefan.jackowski@wel.wat.edu.pl
Polska Agencja Żeglugi Powietrznej, Biuro Rozwoju i Wdrożeń
ul. Wieżowa 8, 02-147 Warszawa, tel.: 022 574 61 64, e-mail: b.kocot@pansa.pl
INTERFERENCE MODELS IN WIRELESS AD-HOC NETWORKS
Abstract: A current models to calculate interference levels in wireless ad-hoc networks with specific modifications are presented. The input parameters for the calculation are the area size, the density of the nodes, the radio propagation conditions (pathloss exponent and standard deviation), the activity ratio of nodes and the MAC protocol class..
1. WPROWADZENIE
Bezprzewodowe sieci typu ad-hoc są od kilku lat jednym z głównych obszarów badań i eksperymentów w radiokomunikacji. Mimo, iż koncepcja organizacji tego typu sieci powstała w latach sześćdziesiątych ubiegłego stulecia, wiele fundamentalnych problemów w ich projektowaniu i implementacji nie zostało dotąd rozwiązanych. Niewątpliwie jednym z nich są powstające w sieci interferencje i związana z tym konieczność retransmisji pakietów. Do tej pory nie opracowano modelu pozwalającego na oszacowanie poziomu interferencji dla sieci typu ad-hoc uwzględniającego rzeczywiste warunki ich pracy. Aktualne modele interferencyjne dla sieci ad-hoc można z punktu widzenia położenia węzłów podzielić na stochastyczne i deterministyczne, zwane dalej analitycznymi. W modelach stochastycznych położenie węzłów w kolejnych chwilach czasowych jest opisywane procesem stochastycznym (w większości przypadków procesem Poissona). W modelach analitycznych położenie węzłów na płaszczyźnie jest ściśle ustalone i nie ulega zmianie w kolejnych chwilach czasowych.
2. MODEL ANALITYCZNY
Rozpatrzmy sieć typu ad-hoc składającą się ze zbioru węzłów rozmieszczonych na danym obszarze w wierzchołkach współśrodkowych sześciokątów foremnych, z gęstością rozmieszczenia ![]()
węzłów na jednostkę powierzchni (rys. 1). Obszar ten nazywany jest obszarem usługowym sieci ad-hoc.
Rys. 1. Struktura sieci ad-hoc wykorzystywana do oszacowania poziomu interferencji
Komunikacja między węzłami odbywa się poprzez kanały radiowe z zanikami. Średnia moc sygnału odbieranego przez dany węzeł, oznaczona przez ![]()
, jest funkcją malejącą ze wzrostem odległości ![]()
między nadajnikiem, a odbiornikiem, zgodnie z zależnością ![]()
, gdzie ![]()
jest współczynnikiem zależnym od mocy sygnału nadawanego, zysku anten nadajnika i odbiornika oraz długości fali, natomiast ![]()
jest współczynnikiem zaników zależnym od środowiska propagacyjnego oraz ukształtowania terenu
i przyjmuje wartości od 2 do 6 (2 dla wolnej przestrzeni, 6 w wielokondygnacyjnych pomieszczeniach zamkniętych). Załóżmy, że w warstwie łącza danych w rozpatrywanej sieci ad-hoc wykorzystywany jest protokół CSMA/CA.
W przyjętej strukturze sieci ad-hoc (rys. 1) na pierwszym obwodzie o promieniu ![]()
rozmieszczonych jest 6 węzłów. Na ![]()
obwodzie o promieniu ![]()
rozmieszczonych będzie ![]()
węzłów. Rozmiar sieci można więc wyrazić za pomocą ![]()
współśrodkowych okręgów wokół węzła 0 lub poprzez całkowitą liczbę węzłów tworzących sieć ![]()
. Te dwa parametry są powiązane ze sobą zależnościami [2]:
![]()
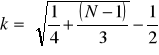
,
gdzie symbol ![]()
oznacza najmniejszą liczbę całkowitą większą od x.
Zdefiniujmy obszar pokrycia danego węzła-nadajnika jako przestrzeń o środku w miejscu rozlokowania danego węzła i promieniu ![]()
, w której moc sygnału odbieranego od tego węzła jest większa bądź równa pewnej wartości progowej ![]()
i odpowiada czułości odbiornika. Liczbę węzłów znajdujących się w obszarze pokrycia danego węzła nazwijmy stopniem tego węzła i oznaczmy przez ![]()
. Zdefiniujmy również zasięg węzła jako liczbę obwodów sześciokątów foremnych zawartych w obszarze pokrycia danego węzła i oznaczmy ją przez ![]()
(przykładowo na rys. 1 zasięg węzła nr 0 wynosi 2). Obszar pokrycia jest obszarem, w obrębie którego dany węzeł może nawiązać bezpośrednią komunikację z dowolnym węzłem znajdującym się w tym obszarze. W przypadku, gdy wymagana jest komunikacja z węzłem znajdującym się poza obszarem pokrycia konieczne jest przekazywanie wiadomości z wykorzystaniem węzłów pośrednich.
Jeżeli zasięg węzła 0 na rys. 1 oznaczymy przez ![]()
, to liczba współśrodkowych obwodów pośrednich z punktu widzenia węzła 0 wynosi ![]()
, gdzie symbol ![]()
oznacza największą liczbę całkowitą mniejszą od x. Liczbę węzłów pośrednich można określić zależnością ![]()
. Średnią liczbę przejść (skoków)
między nadawcą i odbiorcą można określić zależnością
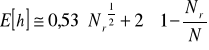
[2].
Na poziom interferencji bezpośredni wpływ ma ruch przenoszony w sieci. Na ruch ten składa się ruch własny generowany przez poszczególne węzły sieci oraz ruch przekazywany między węzłami pośrednimi. Przyjmijmy, że ruch własny generowany przez poszczególne węzły można zamodelować procesem Poissona z intensywnością ![]()
na szczelinę czasową dla każdego węzła sieci. Każdy węzeł rozpatrywanej sieci może być węzłem pośrednim dla ![]()
węzłów, czyli wielkość ruchu przetwarzanego przez każdy węzeł pośredni związany z jego przekazywaniem od nadawcy do odbiorcy wynosi ![]()
. Całkowity ruch generowany i przekazywany przez węzeł sieci można określić zależnością ![]()
[2].
Jeżeli ![]()
jest zasięgiem węzła 0, to liczba współśrodkowych okręgów, na których mogą być rozmieszczone źródła interferencyjne w stosunku do węzła 0 wynosi ![]()
, natomiast liczba węzłów, które mogą generować sygnały zakłócające wynosi ![]()
[2].
W celu oszacowania poziomu interferencji w węźle 0 należy zsumować moce sygnałów odbieranych w węźle 0, które są nadawane przez węzły rozmieszczone na okręgach interferencyjnych. Na pierwszym okręgu interferencyjnym rozmieszczonych jest 6 węzłów w odległości ![]()
. Drugi okrąg interferencyjny składa się z 12 węzłów, z czego 6 węzłów rozmieszczonych w wierzchołkach sześciokąta foremnego znajduje się w odległości ![]()
od węzła 0. Przy oszacowywaniu interferencji przyjęto uproszczenie, że odległość pozostałych 6 węzłów od węzła 0 jest taka sama jak odległość węzłów rozmieszczonych w wierzchołkach sześciokąta. Należy zauważyć, że jest to zbyt daleko idące uproszczenie szczególnie w przypadku, gdy obszar usługowy sieci ad-hoc jest rozległy. Poziom interferencji wyrażany średnią mocą sygnału zakłócającego docierającego do węzła 0 można wyrazić zależnością [2]:
![]()
Gdy liczba węzłów w sieci wzrasta ![]()
powyższa zależność przyjmuje postać [2]:
![]()
,
gdzie dla ![]()
jest funkcją Reimann-Zeta. Dla współczynnika ![]()
jest szeregiem zbieżnym z ograniczeniem górnym [2]
![]()
.
Na podstawie powyższej zależności można oszacować ograniczenie górne poziomu interferencji w sieci ad-hoc opisanej wyżej omówionym modelem zależnością [2]:
![]()
.
Aby możliwy był poprawny odbiór sygnału użytecznego stosunek ![]()
musi być większy od pewnej wartości progowej. W przyjętym modelu równomiernego rozmieszczenia węzłów sieci ad-hoc na obszarze o skończonych rozmiarach najmniejsza wartość sygnału użytecznego dociera do węzła 0 od najdalej położonego na obszarze pokrycia węzła, znajdującego się w odległości ![]()
, natomiast wartość sygnału użytecznego jest największa od najbliżej położonego węzła na obszarze pokrycia, znajdującego się w odległości ![]()
. Wartość średnia sygnału użytecznego uwzględniająca wszystkie możliwe położenia źródła sygnału w stosunku do węzła 0 w jego obszarze pokrycia może być wyrażona zależnością [2]:
![]()
W sieciach typu WLAN, w których wykorzystywana jest technika rozpraszania widma sygnału, poziom interferencji jest uzależniony od zysku przetwarzania ![]()
. Wartość średnia stosunku sygnału użytecznego do poziomu interferencji w tego typu sieciach przyjmuje więc postać [2]:
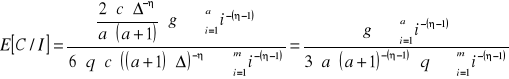
Z powyższej zależności wynika, że wartość średnia stosunku sygnału użytecznego do poziomu interferencji zależy między innymi od prawdopodobieństwa transmisji przez dany węzeł, ![]()
Prawdopodobieństwo to jest związane z wielkością ruchu generowanego i przekazywanego przez dany węzeł. Współczynnik ![]()
można wyrazić więc zależnością ![]()
. Wartość średnia stosunku sygnału użytecznego do poziomu interferencji przyjmuje więc postać [2]:
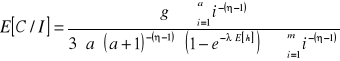
.
3. MODEL STOCHASTYCZNY
Przyjmijmy następujące, upraszczające założenia:
Węzły sieci ad-hoc są równomiernie rozmieszczone na powierzchni koła
o promieniu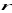
, z gęstością rozmieszczenia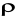
węzłów na jednostkę powierzchni.Transmisja między węzłami odbywa się poprzez kanały radiowe z zanikami wolnymi i pośrednimi. Zaniki wolne związane są (zależnością odwrotne proporcjonalną od odległości między nadajnikiem i odbiornikiem) z poziomem odbieranego sygnału. Zaniki pośrednie modelowane są rozkładem logarytmiczno-normalnym (log-normalnym). Taki model zakłada, że wartości logarytmów z poziomów mocy odbieranego sygnału w odległości
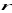
od nadajnika tworzą rozkład normalny z odchyleniem standardowym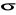
wokół logarytmu ze średniego poziomu mocy odbieranego sygnału.
Dokonajmy oszacowania poziomu sygnału interferującego docierającego do węzła odniesienia rozmieszczonego w środku koła o promieniu ![]()
. Oszacowanie to można podzielić na kilka etapów:
Oszacowanie liczby węzłów interferujących.
Oszacowanie rozmieszczenia węzłów interferujących względem węzła odniesienia.
Oszacowanie poziomów sygnałów interferujących pochodzących z węzłów rozmieszczonych w różnej odległości od węzła odniesienia,
Oszacowanie wartości średniej oraz wariancji wynikowego sygnału zakłócającego z wykorzystaniem różnych metod aproksymacji (FW, Fenton-Wilkinson; SW, Schwarz-Yeh).
Liczba węzłów interferujących oraz gęstość ich rozmieszczenia ![]()
, zależy od liczby wszystkich węzłów tworzących sieć (gęstości ich rozmieszczenia na jednostce powierzchni ![]()
), współczynnika propagacji ![]()
, definiowanego jako stosunek odchylenia standardowego ![]()
wokół logarytmu ze średniego poziomu mocy odbieranego sygnału do współczynnika zaników ![]()
oraz typu protokołu MAC (ang. Medium Access Control). Niska wartość współczynnika ![]()
oznacza małe zmiany poziomu mocy sygnału odbieranego wokół wartości średniej.
Na podstawie badań oraz przeprowadzonych symulacji [1] gęstość rozmieszczenia węzłów interferujących można wyznaczyć z zależności:
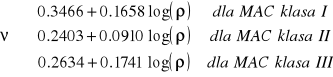
Protokoły MAC w sieciach bezprzewodowych typu ad-hoc można podzielić na trzy klasy, ze względu na sposoby rozwiązywania przez nie problematyki węzłów ukrytych
i odkrytych:
klasa I - protokoły zorientowane na nadajnik: uniemożliwiające nawiązywanie transmisji wszystkim węzłom znajdującym się w obszarze transmisyjnym nadajnika (np. protokół CSMA/CA bez rezerwacji),
klasa II - protokoły zorientowane na nadajnik i odbiornik: uniemożliwiające nawiązywanie transmisji wszystkim węzłom znajdującym się w obszarach transmisyjnych zarówno nadajnika jak i odbiornika (np. protokoły CSMA/CA
z rezerwacją, MARCH, CATS),klasa III - protokoły zorientowane na odbiornik: uniemożliwiające nawiązywanie transmisji wszystkim węzłom znajdującym się w obszarze transmisyjnym odbiornika (np. protokoły RBCS, DBTMA).
Zależność gęstości rozmieszczenia węzłów interferujących od klasy protokołu MAC
w bezprzewodowych sieciach ad-hoc została przedstawiona na rys. 2.
Rys. 2. Zależność gęstości rozmieszczenia węzłów interferujących od klasy protokołu MAC
Przyjmijmy, że węzły interferujące są równomiernie rozmieszczone z gęstością ![]()
wokół węzła odniesienia. Oznaczmy przez ![]()
odległość ![]()
węzła zakłócającego od węzła odniesienia. Na podstawie [1]
![]()
Sygnał nadawany przez każdy m-ty węzeł interferujący rozmieszczony w odległości ![]()
od węzła odniesienia może nie stanowić interferencji dla węzła odniesienia z prawdopodobieństwem 1-![]()
, gdzie ![]()
jest prawdopodobieństwem połączenia między węzłem interferującym a węzłem odniesienia określonym zależnością [ 1]:
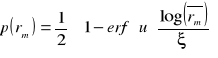
,
gdzie ![]()
, natomiast ![]()
jest odległością znormalizowaną, wyrażoną poprzez zależność ![]()
, gdzie ![]()
jest promieniem obszaru pokrycia węzła odniesienia. Uwzględniając różne poziomy sygnałów zakłócających docierających do węzła odniesienia należy więc przy oszacowywaniu całkowitego poziomu sygnału zakłócającego w węźle odniesienia sumować sygnały pochodzące od różnych węzłów zakłócających z odpowiednim współczynnikiem wagowym, proporcjonalnym do ![]()
. Na podstawie badań i symulacji przedstawionych w [1] współczynnik ten można wyrazić zależnością ![]()
. Współczynnik ten zawiera się w przedziale od 0 do 1. Gdy ![]()
wzrasta, ![]()
maleje, co powoduje zbliżanie się współczynnika ![]()
do wartości 1.
Z przyjętego na wstępie założenia wynika, że poziomy poszczególnych sygnałów zakłócających będą zmiennymi losowymi o rozkładzie log-normalnym. Nie ma matematycznej zależności pozwalającej na dokładne obliczenie sumy tych zmiennych losowych. Istnieją natomiast dwie metody aproksymacji pozwalające wyznaczyć wartość średnią
i odchylenie standardowe zmiennej losowej stanowiącej sumę zmiennych losowych
o rozkładach log-normalnych. Są to: metoda Fenton-Wilkinson (FW) oraz metoda Schwartz-Yeh (SY). Obie metody zakładają, że zmienna losowa stanowiąca sumę zmiennych losowych o rozkładach log-normalnych posiada rozkład log-normalny, natomiast jej wartość średnią i odchylenie standardowe można bezpośrednio wyznaczyć
z wartości średnich i odchyleń standardowych składowych zmiennych losowych. Metoda FW jest stosowana w przypadku, gdy odchylenia standardowe składowych zmiennych losowych spełniają zależność ![]()
, natomiast metoda SY, gdy ![]()
.
Przyjmijmy ![]()
jako zmienną losową stanowiącą poziom sygnału zakłócającego od ![]()
węzła. Zdefiniujmy log-normalne zmienne losowe ![]()
oraz ![]()
. Funkcje gęstości rozkładu prawdopodobieństwa zmiennych losowych ![]()
i ![]()
można wyrazić rozkładami Gaussa z wartościami średnimi odpowiednio ![]()
oraz odchyleniami standardowymi ![]()
. Wartości średnie oraz odchylenia standardowe zmiennych losowych ![]()
powiązane są zależnościami:![]()
. Celem jest znalezienie funkcji gęstości prawdopodobieństwa zmiennej losowej stanowiącej sumę ![]()
zmiennych losowych [1]:
![]()
Metody FW oraz SY aproksymują powyższą sumę w następujący sposób [1]:
![]()
,
gdzie ![]()
jest zmienną losową o rozkładzie Gaussa z wartością średnią oraz odchyleniem standardowym odpowiednio ![]()
. Metoda SY jest zbyt obszerna, nie będzie więc omawiana w ramach niniejszego opracowania. Pewne jej uproszczenie zostało przedstawione w [1].
W metodzie FW ![]()
wyznacza się z momentów pierwszego i drugiego rzędu zmiennej losowej ![]()
zgodnie z poniższymi zależnościami [1]:
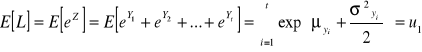
![]()
Wartość średnią i odchylenie standardowe zmiennej losowej ![]()
można następnie wyznaczyć z zależności [1]:
![]()
Rys. 3. Przykładowy przebieg funkcji gęstości prawdopodobieństwa zmiennej losowej stanowiącej wynikowy poziom sygnałów zakłócających w węźle odniesienia
Przykładowy przebieg (uzyskany na podstawie symulacji w [1]) funkcji gęstości prawdopodobieństwa zmiennej losowej Z stanowiącej wynikowy poziom sygnałów zakłócających w węźle odniesienia przedstawiono na rys. 3.
4. PODSUMOWANIE I WNIOSKI
W referacie przedstawiono modele matematyczne (deterministyczny i stochastyczny) pozwalające na oszacowanie poziomu interferencji w bezprzewodowych sieciach typu ad-hoc.
Model deterministyczny został opracowany przy założeniu, że sieć składa się ze zbioru węzłów rozmieszczonych w strukturze współśrodkowych sześciokątów foremnych z gęstością rozmieszczenia q węzłów na jednostkę powierzchni. Przyjęto ponadto założenie modelu kanału radiowego z zanikami wolnymi oraz w warstwie MAC stosowanie protokołu CSMA/CA. Przy takich założeniach uzyskana zależność umożliwiająca oszacowanie poziomu interferencji oraz przeprowadzone symulacje pozwalają na podsumowanie, że dla dużych sieci ad-hoc wartość średnia stosunku ![]()
zmierza do pewnej wartości granicznej (asymptoty), która zależy od współczynnika zaników oraz zasięgu transmisyjnego węzła. Innymi słowy, dla dużych sieci ad-hoc wartość średnia stosunku ![]()
zależy od środowiska propagacyjnego oraz gęstości rozmieszczenia węzłów sieci.
W modelu stochastycznym gęstość rozmieszczenia węzłów interferujących została określona analityczną zależnością, wyznaczoną na podstawie licznych badań i symulacji. Ponadto przyjęto założenie, że model kanału radiowego posiada rozkład logarytmiczno-normalny. Do oszacowania wynikowego poziomu interferencji w bezprzewodowej sieci typu ad-hoc wykorzystano dwie metody aproksymacji (Fenton-Wilkinson - FW oraz Schwartz-Yeh - SY).
Wymienione modele można traktować jako punkt wyjścia do dalszych badań w zakresie ograniczania interferencji w bezprzewodowych sieciach typu ad-hoc.
5. LITERATURA
[1] R. Hekmat: Ad-hoc Networks: Fundamental Properties and Network Topologies, Springer, 2006
[2] R. Hekmat, P. Van Mieghem: Interference in Wireless Multi-hop Ad-hoc Networks and its Effect on Network Capacity. IEEE Trans. on Information Theory, 2005
[3] S. Weber, X. Yang, J. G. Andrews, G. de Veciana: Transmission Capacity of Wireless Ad Hoc Networks with Outage Constraints. IEEE Trans. on Information Theory, 2004
[4] S. De, Ch. Qiao, D. A. Pados, M. Chatterjee: Topological and MAI Constraints on the Performance of Wireless CDMA Sensor Networks. IEEE INFOCOM, 2004
[5] A. Hasan, J. G. Andrews: The Critical Radius in CDMA Ad hoc Networks. IEEE Trans. on Information Theory, 2005
[6] B. H. Liu, Ch. T. Chou, J. Lipman, S. Jha: Using Frequency Division to Reduce MAI in DS-CDMA Wireless sensor Networks. IEEE Trans. on Information Theory, 2005
[7] T. Moscibroda, R. Wattenhofer: Minimizing Interference in Ad Hoc and Sensor Networks. DIALM-POMC'05, September 2005
[8] K. Moaveni-Nejad, X. Y. Li: Low-Interference Topology Control for Wireless Ad Hoc Networks. IEEE Trans. on Information Theory, 2002
[9] S. Gobriel, R. Melhem, D. Mosse: A Unified Interference/Collision Analysis for Power-Aware Adhoc Networks. IEEE Trans. on Information Theory, 2004
[10] R. Hekmat, P. Van Mieghem: Interference Power Sum with Log-normal Components in Ad-hoc and Sensor Networks. IEEE Trans. on Information Theory, 2002
1
![]()
Wyszukiwarka
Podobne podstrony:
ETYKA w ZARZĄDZANIU dla studentów WSB
filozofia + redniowieczna wsb
Ściaga Jackowski
Sesja poprawkowa II rok SUM SP, WSB ( WYŻSZA SZKOŁA BANKOWA)
DOM PRAWA kodeksy, STUDIA, WSB, prawo
Socjalizm utopijny, Materiały dla studentów WSB DG
Pytania z przedmiotu PR dla studentów, STUDIA WSB GDAŃSK, PR
prawo 8 grudnia, wsb-gda, Elementy prawa
LISTA 2 zaoczne, WSB ( WYŻSZA SZKOŁA BANKOWA)
zagadn do zalicz - wsb, WSB Chorzów, SYSTEMY PODATKOWE TESTY
Rozwój bankowości w Polsce, FINANSE I RACHUNKOWOŚĆ, WSB gda, Bankowość (figiela)
sciaga socjologia, wsb-gda, Podstawy socjologii
wzor profesjonalne CV, Zarządzanie - Zarządzanie Zasobami Ludzkimi WSB Chorzów, Semestr Sesja 4, Wpr
prawo1, WSB, MGR, prawo cywilne
ubezpieczenia, WSB GDA, Ubezpieczenia społeczne
logika WSB
więcej podobnych podstron