§ 13 Całka oznaczona Riemanna
Niech funkcja rzeczywista f będzie określona i ograniczona na przedziale <a,b>.
Dzielimy przedział <a,b>przy pomocy punktów:
![]()
na przedziale ![]()
i = 0, 1, ..., n-1. Oznaczmy przez x największą z różnic ![]()
tzn.
![]()
i = 0, 1, ..., n-1
Liczbę ![]()
nazywamy średnią podziału przedziału<a,b>. W każdym z przedziałów częściowych ![]()
obieramy dowolny punkt ![]()
.(„![]()
” - ksi) ![]()
Tworzymy sumę całkową postaci ![]()
Można utożsamić podział przedziału <a,b>na przedziały częściowe punktami: ![]()
Z układami punktów działowych ![]()
Wtedy możemy rozważać ciąg podziałów ( Πm ) przedziału<a,b>, przy czym ![]()
nm- liczba naturalna.
Mówimy, że ciąg podziałów ( Πm ) przedziału <a,b> na przedziały częściowe jest ciągiem normalnym, jeżeli odpowiadający mu ciąg średnic ![]()
jest zbieżny do zera.
Definicja: Jeżeli przy dowolnym ciągu normalnym podziałów przedziału <a,b> oraz przy dowolnym wyborze punktów pośrednich ![]()
ciąg sum całkowitych postaci ![]()
Dążą zawsze do skończonej granicy równej liczbie I to granicę tę nazywamy całką oznaczoną funkcji f na przedziale ![]()
i oznaczamy symbolem I =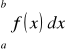
.
W przypadku, gdy granica ta istnieje funkcją f nazywamy całkowalną na przedziale<a,b>.Liczby a, b nazywamy odpowiednio dolną i górną granicą całkowania.Ponieważ def pochodzi od b Riemanna (XIX) stąd mówimy o całce oznaczonej Riemanna oraz o całkowalności w sensie Riemanna.Niech f(x)≥0 dla każdego x∈<a,b>. Wtedy suma całkowa
![]()
jest równa sumie pól prostokątów o wartości f(![]()
) i długości podstawy ![]()
Zatem całka oznaczona 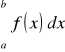
jako granica ciągu sum całkowych postaci ![]()
jest równe polu obszaru płaskiego ograniczonego łukiem krzywej y = f(x) x∈<a,b>odcinkami prostych x = a, x = b oraz osi OX i <a,b>
Własności całki oznaczonej.
Jeżeli funkcja f, g są całkowalna na przedziale <a,b> to kombinacja liniowa αf +βf, gdzie α, β stałe, jest całkowalna na <a,b> oraz
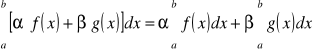
Jeżeli funkcja f jest całkowalna na <a,b> oraz
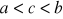
to f jest całkowalna na każdym z przedziałów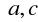
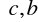
oraz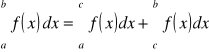
Jeżeli f jest całkowalna na <a,b> to f jest też całkowalna na przedziale
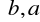
oraz
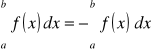
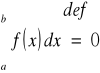
Jeżeli funkcja f jest całkowalna na <a,b> gdzie a<b oraz f(x) ≥0 dla x∈<a,b> to
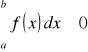
W przypadku, gdy f(x) > 0 dla x∈<a,b> to 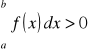
Jeżeli funkcja f, g są całkowalne na <a,b> a<b oraz dla każdego x∈<a,b> f(x) ≤ g(x) ( f(x) < g(x)) to
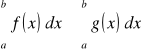
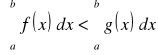
Niech funkcja f będzie całkowalna na <a,b> a<b. Wtedy funkcja f jest całkowalna na <a,b> oraz zachodzi nierówność
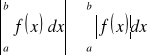
.Jeżeli funkcja jest całkowalna na <a,b> a<b oraz dla każdego x∈<a,b> m ≤ f(x) ≤ M gdzie m, M są stałymi to zachodzi nierówność
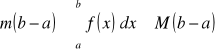
Jeżeli:
funkcje f, g są całkowalne na <a,b>
dla każdego x∈<a,b>
m ≤ f(x) ≤ M
g(x) ≥ 0 (lub g(x) > 0 ) dla każdego x∈<a,b> tzn. funkcja g ma stały znak w całym przedziale <a,b> to
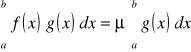
gdzie ![]()
W szczególności, gdy g(x) = 1 otrzymujemy 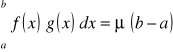
![]()
Można wykazać, że:
Każda funkcja ciągła f na przedziale <a,b> jest całkowalna w sensie Riemmana na <a,b>
Jeżeli funkcja f jest ogromna na <a,b>oraz posiada w tym przedziale skończoną liczbę punktów nieciągłości I - go rodzaju, to f jest całkowalna na <a,b>
Funkcja f ograniczona i monotoniczna na<a,b> jest całkowalna na tym przedziale.
Sposoby odliczania całek oznaczonych
Twierdzenie 1 (Wzór Newtona - Liebnica)
Jeżeli funkcja rzeczywista jest całkowalna w sensie Riemmana na przedziale <a,b> oraz posiada skończoną funkcję pierwotną F dla każdego x∈<a,b>
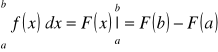
Dowód.
Dokonujemy podziału ![]()
przedziału<a,b>. Na podstawie twierdzenia Legrange'a o wartości średniej istnieją takie punkty ![]()
∈ ![]()
i = 1, 2,..., n że:
![]()
dla i = 1, 2,..., n
Stąd otrzymujemy
![]()
Ponadto zachodzi równość
![]()
![]()
![]()
Dowód.Zatem dla dowolnego ciągu naturalnego podziałów przedziału <a,b> można dla każdego podziału z osobna dobrać punkty pośrednie ![]()
tak, by zachodziła równość
![]()
Zbadany w ten sposób ciąg sum całkowych ![]()
dąży do granicy F(b) - F9a).
Ponieważ f jest całkowalna na <a,b> więc ciąg ten dąży do całki 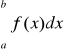
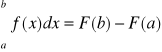
Przykład 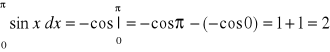
Twierdzenie 2 (Całkowanie przez części)
Jeżeli funkcja f, g posiada ciągłe pochodne na przedziale <a,b> to
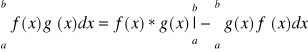
gdzie![]()
Twierdzenie 3 (Całkowanie przez części)
Jeżeli: Funkcja f, g jest cięgła na przedziale <a,b>
Funkcja ϕ jest określony na przedziale ![]()
przy czym dla każdego t ∈![]()
to: 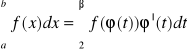
ZASTOSOWANIE CAŁEK OZNACZONYCH.
Niech będzie dana krzywa w postaci parametrycznej (1) ![]()
, ![]()
, ![]()
dla ![]()
przy czym pochodne ![]()
są ciągłe w![]()
.
Punktem osobliwym krzywej (1) nazywamy punkt odpowiadający parametrowy ![]()
taki, że ![]()
. Dla punktów osobliwych krzywej (1) zaliczamy również punkty wielokrotne tzn. punkty które otrzymujemy dla dwóch lub większej liczby wartości parametrów. Zakładamy, że krzywe o których mowa poniżej nie zawierają punktów osobliwych z wyjątkiem co najwyżej pokrywających się końców krzywej zamkniętej.
1. Pole obszaru płaskiego
Pole obszaru płaskiego ABCD ograniczonego krzywymi y=f1(x), y=f2(x) gdzie f1,f2 są funkcjami ciągłymi na <a,b>, f2(x)≥f1(x) dla ![]()
oraz prostymi x=a, x=b jest równe
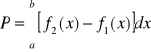
Jeżeli krzywa k dana jest w postaci parametrycznej k: ![]()
, ![]()
dla ![]()
funkcje ![]()
są ciągłe, przy czym ![]()
jest ciągła na ![]()
![]()
dla ![]()
to pole obszaru płaskiego ograniczonego tą krzywą, odcinkiem OX oraz prostymi ![]()
jest równe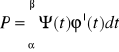
Niech będzie dany układ prostokątny OXY na płaszczyźnie. Każdy punkt P płaszczyzny jest jednoznacznie kreślony przez podanie uporządkowanej pary współrzędnych P=(x0,y0). Punkt P jednoznacznie określa także następujące wielkości r=|OP| - odległość punktu P od początku układu OXY. φ - miara kąta między półosią OX i promieniem wodzącym OP punktu P
Współrzędnymi biegunowymi punktu P nazywamy uporządkowaną parę (r, φ). Wtedy punkt O nazywamy biegunem, a półprostą OX nazywamy osią biegunową.Związek między współrzędnymi prostokątnymi i biegunowymi punktu P jest następujący:
x0=rcos φ
y0=rsin φ
Pole figury OAB ograniczonej krzywą k daną we współrzędnych biegunowych ![]()
dla ![]()
, ![]()
gdzie ![]()
jest nieujemną funkcją ciągłą na ![]()
oraz promieniami wodzącymi OA, OB. odpowiadającymi wartościom ![]()
wynosi: 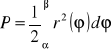
2. Objętość bryły oraz pole powierzchni obrotowej.
Jeżeli s=s(x), xε![]()
jest funkcją ciągła wyrażającą pole przekroju bryły płaszczyzną prostopadłą do osi O, to objętość bryły zawartej między płaszczyznami x=a, x=b wynosi 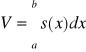
Przykład: Obliczyć objętość bryły ograniczonej elipsoidą trójosiową ![]()
Objętość bryły obrotowej powstałej na skutek obrotu ciągłej nieujemnej krzywej y=f(x) xε<a,b>, dokoła osi OX wynosi: 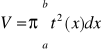
Pole powierzchni bocznej bryły obrotowej powstałej na skutek obrotu krzywej ![]()
, ![]()
dla ![]()
dokoła osi OX przy czym ![]()
są ciągłe na ![]()
wynosi: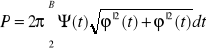
3. Długość krzywej
Niech będzie krzywą o przedstawieniu parametrycznym ![]()
, ![]()
, ![]()
dla ![]()
. Oznaczmy przez ![]()
dowolny podział przedziału ![]()
. Niech ![]()
oznaczmy przez ![]()
łamaną o węzłach w punktach p0,p1,...pn
Definicja: Długością S krzywej k nazywamy wielkości ![]()
jest długością łamanej ![]()
. Jeżeli zbiór ![]()
jest ograniczony, to ![]()
Wtedy krzywą k nazywamy prostoliniową lub rektyfikowalną. Jeżeli zbiór długości łamanych ![]()
jest nieograniczony to przyjmujemy ![]()
Twierdzenie 1.
Jeżeli krzywa AB jest postaci ![]()
, ![]()
, ![]()
dla ![]()
, gdzie ![]()
są ciągłe na ![]()
, bez punktów osobliwych z wyjątkiem co najwyżej pokrywających się końców krzywej, to krzywa AB jest prostoliniowa.
Dowód: W krzywą AB wpisujemy łamaną o wierzchołkach: M0,M1,.....Mn które odpowiadają wartościom parametru ![]()
. Oznacza to, że punkt Mi iε{0,1,...,n}, ma współrzędne ![]()
Długość łamanej wynosi ![]()
Z twierdzenia Lagrangea o wartości średniej wynika, że:
![]()
![]()
![]()
![]()
stąd ![]()
Oznaczmy odpowiednio przez ![]()
największe wartości funkcji ciągłych ![]()
na przedziale ![]()
.Wtedy ![]()
![]()
Zatem zbiór długości łamanych opisanych w krzywą AB jest ograniczony z góry, tzn, krzywa AB ma skróconą długość, czyli jest prostoliniowa.
Wniosek: Długość krzywej AB można oszacować następująco : ![]()
oznaczając odpowiednio przez ![]()
najmniejsze wartości funkcji ciągłych ![]()
na przedziale ![]()
otrzymujemy następujące oszacowania z dołu dla długości krzywej AB ![]()
Rozważmy dla krzywej z twierdzenia pierwszego zamiast przedziału ![]()
przedział częściowy ![]()
gdzie ![]()
, Δt>0 Wtedy przedziałowi ![]()
odpowiada łuk krzywej AB o długości Δs. Ponadto zachodzą oszacowania: ![]()
gdzie ![]()
- odpowiednio najmniejsze oraz największe wartości funkcji ciągłej ![]()
na przedziale![]()
stąd otrzymujemy: ![]()
przy ![]()
otrzymujemy ![]()
. Analogicznie postępujemy w przypadku przedziału ![]()
Δt >0. Jeżeli ![]()
lub ![]()
to obliczamy pochodną jednostronną funkcji ![]()
.
Jeżeli parametr t zmienia się w przedziale ![]()
a wraz z nim położenie punktu M=M(t) na krzywej AB (z twierdzenia 1) to długość zmiennego łuku AM jest funkcją parametru t. Oznaczmy tę funkcję przez s=s(t) dla ![]()
Z (1) wynika, że funkcja jest różniczkowalna. Widać, że ![]()
. Korzystając ze wzoru Newtona-Leibniza otrzymujemy 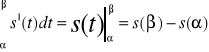
= długości krzywej AB=S czyli 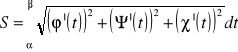
.
Jeżeli płaska krzywa AB dana jest w postaci y=f(x) dla xε<a,b> gdzie f| jest ciągła na <a,b> to przyjmując x jako parametr otrzymujemy postać parametryczną krzywej AB|: x=x, y=f(x) dla xε<a,b>. Stąd długość łuku krzywej AB wynosi:
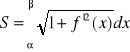
Jeżeli krzywa płaska AB dana jest równaniem we współrzędnych biegunowych r=r(φ) dla φε< φ1, φ2> gdzie r| jest ciągła na < φ1, φ2> to jej przedstawienie parametryczne ma postać x=r(φ)cosφ, y=r(φ)sin φ, φε< φ1, φ2> kolejno otrzymujemy:
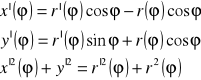
stąd 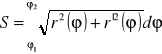
53
Wyszukiwarka
Podobne podstrony:
Wyklady z Matematyki czesc IV, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc V, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc II, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc I, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc III, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc III, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VII do mdruku, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykład
Wyklady z Matematyki czesc V, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z matematyki IV sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
Wyklady z matematyki IV, MATMA, Matma
Wyklady z matematyki II sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
Z Wykład 15.03.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Wykład z dnia 10.05.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
Z Wykład 19.04.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Wykład 23.02.2008, Zajęcia, II semestr 2008, Analiza matematyczna
WYKŁAD Mechanika Ogólna Część IV
część IV Wykład och zao 5
więcej podobnych podstron