LABORATORIUM FIZYKI I |
Ćwiczenie nr: 37 |
|||
|
Data: 31.10.08 |
|||
Wydział: SiMR |
Grupa: 2.3 |
Zespół: 4 |
Punktacja: |
Przygotowanie:
|
Nazwisko i Imię: Demidowski Tomasz |
|
|
||
Temat ćwiczenia: Zjawisko skręcenia płaszczyzny polaryzacji światła
|
|
Sprawozdanie:
|
||
Prowadzący:
|
|
Suma punktów:
|
||
Wstęp teoretyczny
Celem niniejszego ćwiczenia było zapoznanie się ze zjawiskiem polaryzacji światła, metod polaryzacji światła oraz przyczyny występowania skręcenia płaszczyzny polaryzacji w niektórych substancjach.
Światło to fala elektromagnetyczna, zdolna do przenoszenia energii, ulegająca zjawiskom charakterystycznym dla ruchu falowego (np. interferencja, dyfrakcja). W przypadku oddziaływanie z elektronami zachowuje się jak strumień cząstek (fotonów).
Fala elektromagnetyczna to rozchodzący się w przestrzeni ciąg zmiennych pól elektrycznych i magnetycznych wzajemnie się wytwarzających. Fala taka opisana jest przez wektor pola elektrycznego (![]()
), wektor indukcji pola magnetycznego (![]()
) oraz wektor falowy określający kierunek rozchodzenia się fali (![]()
, gdzie λ to długość fali).
Wektory ![]()
, ![]()
, ![]()
są do siebie wzajemnie prostopadle. Powoduje to, że fala elektromagnetyczna jest falą poprzeczną.
Polaryzacja to własność fali poprzecznej (np. światła). Polega ona na tym, że drgania wektora natężenia pola elektrycznego zachodzą tylko w pewnym wybranym kierunku. Fala niespolaryzowana oscyluje we wszystkich kierunkach jednakowo. Występuje kilka rodzaji polaryzacji:
- polaryzacja liniowa - drgania wektora natężenia pola elektrycznego zachodzą tylko w jednej płaszczyźnie, która nie zmienia swojego położenia w przestrzeni
- polaryzacja kołowa lub eliptyczna - koniec wektora natężenia pola elektrycznego fali opisuje linię śrubową kołowa lub eliptyczną
Liniowo Spolaryzowane światło można uzyskać stosując kilka różnych metod polaryzacji:
- za pomocą błon polaryzujących (polaroidów) - przeźroczysta, rozciągniętą i nasycona w roztworze jodu błona wykonana z alkoholu poliwinylowego pochłania drgania elektryczne zachodzące w kierunku równoległym do kierunku ustawienia łańcuchów cząstek polimerów i jodu. Natomiast drgania w kierunku prostopadłym są przepuszczane bez znacznej straty energii
- za pomocą polaryzatorów odbiciowych - światło spolaryzowane uzyskuje się w wyniku odbicia od dielektryka. Aby wiązka odbita była całkowicie spolaryzowana kąt jest padania musi być równy kątowi Brewstera. Przypadek ten zachodzi, gdy wiązka odbita jest prostopadła do wiązki załamanej. W takiej sytuacji współczynnik załamania musi być równy: n=tgαBr
- za pomocą polaryzatorów dwójłomnych - w kryształach dwójłomnych zachodzi zjawisko podwójnego załamania w wyniku, czego uzyskuje się 2 wiązki załamane: zwyczajna i nadzwyczajną. Wiązka zwyczajna ma stał prędkość niezależna od kierunku rozchodzenia się w krysztale. Spełnia prawo Snelliusa. Prędkość drugiej wiązki zależy od tego, w jakim kierunku propaguje, zatem stosunek ![]()
nie jest stały. Współczynnik załamania dla tej fali określa się jako stosunek prędkości fali w próżni do prędkości fali nadzwyczajne w krysztale.
Prędkość fali nadzwyczajne zależy od kata między kierunkiem wiązki światła, a osią optyczną ciała.
W celu uzyskania jednej wiązki załamanej używa się pryzmatu Nicola. W takim układzie optycznym wiązka zwyczajna ulega całkowitemu odbiciu wewnętrznemu i jest pochłaniana przez zaczernione boczne ścianki nikola. Wiązka nadzwyczajna ulega tylko nieznacznemu osłabieniu przez odbicie i wychodzi z pryzmatu równolegle do kierunku padania.
Pewne kryształy poza zjawiskiem dwójłomności wykazują także zdolność do skręcania płaszczyzny drgań światła biegnącego w kierunku osi optycznej danego ciała. Cecha taka nazywa się naturalna aktywnością optyczną. Aktywność optyczna wykazują ponadto, niektóre ciecze np. terpentyna, nikotyna oraz roztwory ciał stałych w cieczach optycznie nieaktywnych (no roztwór cukru w wodzie). Zależność na kąt skręcenia płaszczyzny opisana jest wzorem:
![]()
Gdzie:
![]()
- kąt skręcenia płaszczyzny polaryzacji
![]()
- skręcenie właściwe
c - stężenie roztworu
h- grubość warstwy roztworu
Współczynnik skręcenia właściwego γ zależy od długości fali padającego światła.
Ciała nieaktywnie optyczne umieszczone w polu magnetycznym, będą zachowywać się jak ciała aktywnie optycznie, czyli będą powodować skręcenie płaszczyzny drgań. Zjawiskiem tym zajmował się Michael Faraday. Ustalił on, że kąt skręcenia płaszczyzny polaryzacji zależy od kąta pomiędzy kierunkiem rozchodzenia się fali, a kierunkiem wektora indukcji magnetycznej. Wzór opisujący zjawisko Faradya wygląda następująco:
![]()
![]()
- kąt skręcenia płaszczyzny polaryzacji
V- stała Verdeta
B - wartość indukcji magnetycznej
h - grubość warstwy roztworu
Stałą Verdeta w tym wzorze zależy bardzo silnie od długości fali świetlnej, a także od gęstości ośrodka i temperatury. W zależności od znaku stałej Verder, wyróżnia się ciała lewo i prawoskrętne. Do ciał lewoskrętnych zalicza się większość diamagnetyków i paramagnetyków.
Układ pomiarowy
Do pobadania zjawiska naturalnej aktywności optycznej użyliśmy polarymetru półcieniowego.
Światło ze źródła Z (w naszym przypadku lampa sodowa emitującą światło o długości λ=589,3 [nm]) przechodzi przez polaryzator P i pada na przesłonę D, w której zostały wycięty kulisty otwór. Połowa otworu zasłonięta jest przez płytkę kwarcową Laurneta. W rurce T znajduje się badana ciecz. Długość rurki jest równa długości drogi przebytej przez światło w badanej cieczy, czyli h=156 [mm]. Za rurka ustawiony jest analizator (nuncjusz), którego zadaniem jest badanie kąta skręcenia płaszczyzny. Na końcu układu znajduje się obiektyw i okular lunetki, przez które prowadzi się obserwację
W drugiej części naszym zadaniem było badanie aktywności optycznej wywołanej polem magnetycznym. Tu także użyliśmy polarymetru, z ta różnica ze rurka nie była wypełniona roztworem cukru, ale szklanym prętem o długości h=156 [mm]. Ponadto skręcanie płaszczyzny drgań wywołuje polem magnetyczne powstałe na skutek przepływu prądy przez uzwojenie solenoidu, wewnątrz którego znajduje się polarymetr. Solenoid użyty podczas ćwiczenia posiadał N=3623 zwojów i długość L=280 [mm].
Wykonanie ćwiczenia
a) Badanie naturalnej aktywność optycznej.
Włączenie zasilacza lampy sodowej i odczekanie około 5 min do rozgrzania lampy i uzyskania pełnej jasności.
Napełnieni polarymetru wodą destylowaną. Zakręcenie górnej pokrywki. Sprawdzenie czy w zbiorniku nie ma pęcherzyków powietrza oraz czy soczewki są suche.
Włożenie kuwety z woda destylowaną do polarymetru. Ustawienie analizatora w taki sposób, aby wszystkie 3 części pola widzenia miały jednakową jasność
Odczytanie ze skali nuncjusza kąta, czyli położenia zerowego analizatora α0 dla wody.
Przygotowanie roztworów o 6 różnych stężeniach, poprzez rozpuszczenie w 50 ml wody 1,2,4,6,8 i 10 g cukru.
Napełnianie kuwety kolejno każdym z badanych roztworów, za zachowaniem uwagi żeby po każdym pomiarze przepłukać dwukrotnie kuwetę.
Zbiornik z roztworem umieszczamy w polarymetrze i mierzymy wartość analizatora αp. obliczamy kąt skręcenia płaszczyzny drgań α= αp- α0.
Pomiar długości kuwety i oszacowanie błędu pomiaru.
b) Badanie zjawiska Faradaya
Włączenie zasilania lampy sodowej. Odczekanie 5 min do rozgrzania lampy i uzyskania pełnej jasności świecenia.
Przy wyłączonym zasilaczu cewki (brak pola magnetycznego) mierzymy kat skręcenia płaszczyzny α0 dla pręta szklanego.
Włączenie zasilania solenoidu.
Pomiar kąt nowego położenia analizatora αp dla 6 różnych wartość natężenia prądu. Obliczenie wartości kata skręcenia α= αp- α0.
Opracowanie wyników
Badanie naturalnej aktywność optycznej.
W pierwszej części naszym zadaniem było zbadanie zależności kąta skręcenia płaszczyzny polaryzacji w zależności od stężenia roztworu cukru w wodzie. W tym celu zbadaliśmy kąt skręcenia dla 6 różnych stężeń roztworu.
Pomiar: |
Stężenie roztworu [%] |
Kąt skręcenia α [0] |
Kąt skręcenia α [rad] |
1 |
0 |
0 |
0 |
2 |
1,961 |
2 |
0,035 |
3 |
3,846 |
3,85 |
0,067 |
4 |
7,407 |
7,4 |
0,129 |
5 |
10,714 |
10,8 |
0,188 |
6 |
13,793 |
14,155 |
0,247 |
7 |
16,667 |
17,55 |
0,306 |
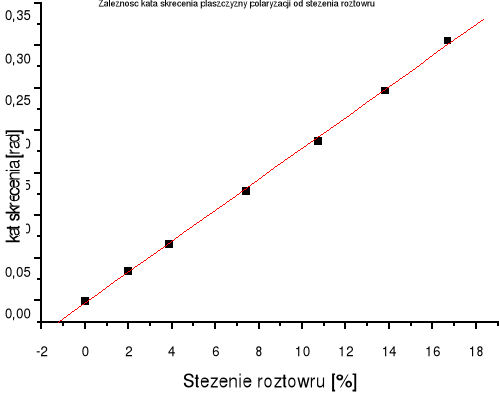
Na podstawie danych pomiarowych wykonaliśmy w programie ORIGN wykres zależności kąta skręcenia od stężenia roztworu. Zależność ta jest opisana wzorem:
![]()
Gdzie:
![]()
- kąt skręcenia płaszczyzny polaryzacji
![]()
- skręcenie właściwe
c - stężenie roztworu
h - grubość warstwy roztworu
Następnie korzystając z metody sumy najmniejszych kwadratów i podstawiając:
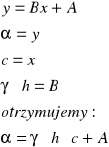
Program ORIGIN znajduje prostą, która w najlepszy sposób pokrywa się z punktami pomiarowymi na sporządzonym wykresie. Znając współczynnik kierunkowy prostej możemy wyznaczyć współczynnik skręcenia właściwego.
2008-11-02 12:50
Linear Regression for Data1_B:
Y = A + B * X
Parameter Value Error
------------------------------------------------------------
A -0,00244 0,00237
B 0,01819 2,44433E-4
------------------------------------------------------------
R SD N P
------------------------------------------------------------
0,99955 0,00374 7 <0.0001
------------------------------------------------------------
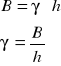
W naszym przypadku:
B=0,01819
H=156 [mm]=0,156 [m]
Zatem:
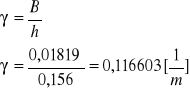
W celu wyliczenia różnicy współczynników załamania fali spolaryzowanej prawo i lewoskrętnie w funkcji stężenia skorzystam ze wzoru:
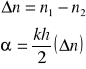
Gdzie:
N1 - współczynnik załamania fali spolaryzowanej kołowo prawoskrętnie
N2 - współczynnik załamania fali spolaryzowanej kołowo lewoskrętnie
K - wektor falowy
H - grubość warstwy roztworu
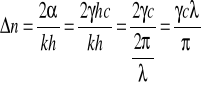
Dla 3 pomiaru:
C=3,846 [%]=0,03846
λ=589,3 [nm] =589,3x10-9 [m]
γ=0,116603 [1/m]
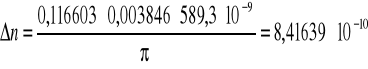
Badanie zjawiska Faradaya
Drugiej części ćwiczenia zajmowaliśmy się zjawiskiem Faradaya. Zmieniając natężenie prądu przepływającego przez cewkę, a co za tym idzie także wartość indukcji magnetycznej B, obserwowaliśmy zmianę kąta skręcenia płaszczyzny polaryzacji. Wyniki pomiarów zostały przedstawione w tabeli.
Pomiar |
I [A] |
Kąt skręcenia |
Kąt skręcenia [rad] |
B [T] |
1 |
0 |
0 |
0,00000 |
0,00000 |
2 |
1 |
2,3 |
0,04014 |
0,01626 |
3 |
2 |
4,8 |
0,08378 |
0,03252 |
4 |
3 |
7,9 |
0,13788 |
0,04878 |
5 |
4 |
9,8 |
0,17104 |
0,06504 |
6 |
5 |
13,2 |
0,23038 |
0,08130 |
7 |
6 |
14,8 |
0,25831 |
0,09756 |
W ostatniej kolumnie została wyznaczona wartość indukcji magnetycznej odpowiadającej danej wartość natężenia prądu przepływającego przez cewkę. Wartość tą znajdujemy z wzoru:
![]()
Gdzie:
![]()
- przenikalność magnetyczna próżni
I - natężenie prądu
N - liczba zwojów cewki (N=3623)
L - długość cewki (L=280 [mm]=0,28 [m])
Dla 4 pomiaru:
I=4 [A]
![]()
Na podstawie pomiarów sporządziliśmy wykres zależności kąta skręcenia α od wartości natężenia prądu I w solenoidzie. Zależność ta opisuje wzór:
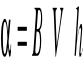
![]()
- kąt skręcenia płaszczyzny polaryzacji
V- stała Verdeta
B - wartość indukcji magnetycznej
h - grubość warstwy roztworu
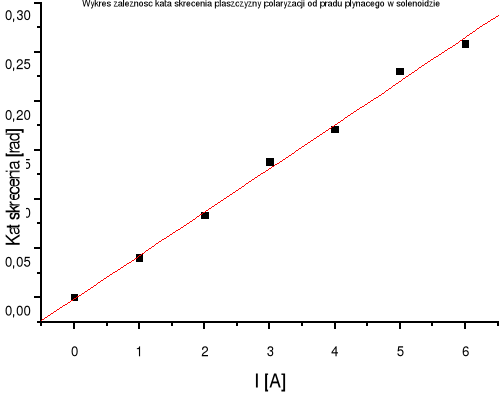
2008-11-02 14:41
Linear Regression for Data1_B:
Y = A + B * X
Parameter Value Error
------------------------------------------------------------
A -0,0015 0,00459
B 0,04438 0,00127
------------------------------------------------------------
R SD N P
------------------------------------------------------------
0,99795 0,00674 7 <0.0001
------------------------------------------------------------
Nastepnie sporządziliśmy wykres zależności kąta skręcenia α od wartości indukcji pola magnetycznego B wytworzonego w solenoidzie przez prąd I.
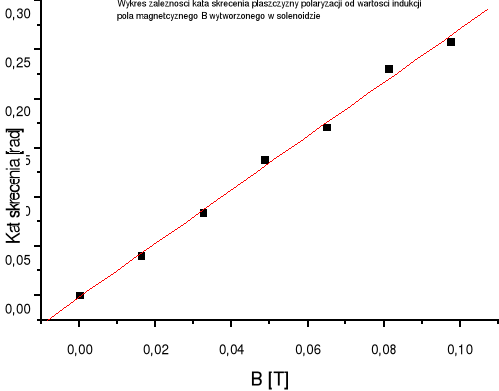
2008-11-05 18:24
Linear Regression for Data1_B:
Y = A + B * X
Parameter Value Error
------------------------------------------------------------
A -0,0015 0,00459
B 2,72946 0,07832
------------------------------------------------------------
R SD N P
------------------------------------------------------------
0,99795 0,00674 7 <0.0001
------------------------------------------------------------
Następnie korzystając z metody sumy najmniejszych kwadratów i podstawiając:
![]()
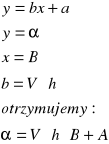
Program ORIGIN znajduje prostą, która w najlepszy sposób pokrywa się z punktami pomiarowymi na sporządzonym wykresie. Znając współczynnik kierunkowy prostej możemy wyznaczyć stała Verdeta.
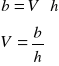
w naszym przypadku:
h- 156 [mm]=0,156 [m]
b=2,72946
![]()
Znając stała Verdeta, możemy obliczyć wartość ![]()
. W tym celu skorzystamy z zależności:
![]()
Gdzie:
e- ładunek elektronu
me - masa elektronu
λ- długość fali
c- prędkość światła
![]()
- zmiana współczynnika załamania światła względem długości fali.
Powyższa wartość można obliczyć z wyrażenia ![]()
, gdzie n1,n2 to współczynnika załamania fal λ 1, λ 2 pomiędzy którymi leży długość fali światła λ użytego w doświadczeniu.
Wartość współczynników odczytaliśmy z tabliczki znajdującej się przy stanowisku, dla światła o długości 100nm mniejszej i większej od rzeczywistej jego wartości.
λ 1=689,3 [nm]
n1=1,613
λ 2=489,3 [nm]
n2=1,6315
λ=589,3 [nm]
n=1,62
Zatem:
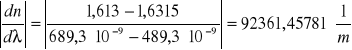
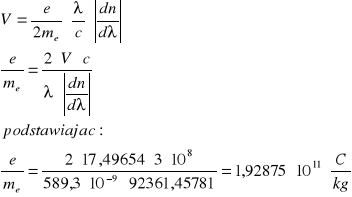
Rachunek błędów
Badanie naturalnej aktywność optycznej.
Wyznaczona wartość współczynnika skręcenia właściwego obarczona jest błędami systematycznymi i przypadkowymi. Wynikają one z niedokładność urządzeń pomiarowych (nuncjusz) oraz metody sumy najmniejszych kwadratów.
Błąd wartości skręcenia właściwego wyznaczamy różniczki zupełnej (wielkość wyznaczana w sposób pośredni).
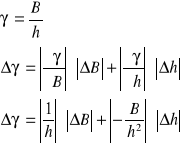
Program Origin oblicza średni błąd kwadratowy δB bez uwzględnienia współczynnika t-Studenta, stąd aby uzyskać jego prawidłową wartość należy pomnożyć średni błąd kwadratowy przez współczynnik t(![]()
,k).
k = n - 2
Gdzie: n - liczba pomiarów
k = 7 - 2 = 5
Przyjmuję współczynnik ufności![]()
0.9
t(![]()
, k) = t(0.9,5) = 2,015 (z tabeli)
δB =2,44433x10-4
δBp = δB t(β,k) =2,44433x10-4 x 2,015 = 4,92532x10-4
Podstawiając wartości:
![]()
=1 [mm]=0,001[m]
δBp =2,44433x10-4
h=0,156[m]
B=0,01819
Otrzymujemy;
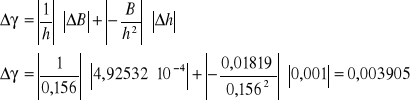
Zatem ostateczna wartość współczynnika skręcenia właściwego wynosi:
![]()
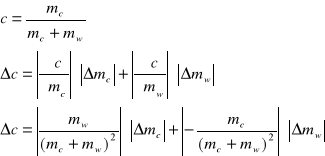
W celu wyznaczenia błędu różnicy współczynników załamania fali spolaryzowanej prawo i lewoskrętnie także korzystamy z różniczki zupełnej.
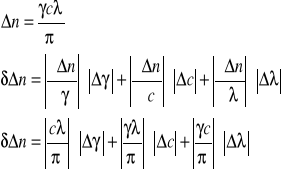
Niedokładność pomiaru stężenia roztworu wynika z błędów systematycznych pomiaru masy cukru i wody.
Dla 3 pomiaru:
Mc=3 [g]=0,003 [kg]
Mw=50 [g]=0,05 [kg]
![]()
= ![]()
=0,01 [g]=1x10-5 [kg]
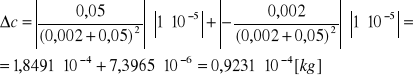
Dla 3 pomiaru:
C=3,846 [%]=0,03846
λ=589,3 [nm] =589,3x10-9 [m]
γ=0,116603 [1/m]
![]()
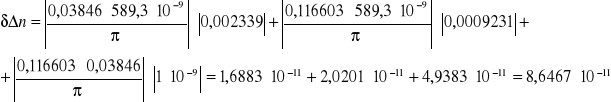
Ostateczna wartość różnicy współczynników załamania fali spolaryzowanej prawo i lewoskrętnie wynosi:
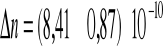
Badanie zjawiska Faradaya
Wyznaczona przez nas wartość stałej Verdeta obarczona jest błędami, których wielkość można wyznaczyć korzystając z różniczki zupełnej:
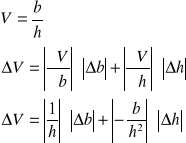
Program Origin oblicza średni błąd kwadratowy δB bez uwzględnienia współczynnika t-Studenta, stąd aby uzyskać jego prawidłową wartość należy pomnożyć średni błąd kwadratowy przez współczynnik t(![]()
,k).
k = n - 2
Gdzie: n - liczba pomiarów
k = 7 - 2 = 5
Przyjmuję współczynnik ufności![]()
0.9
t(![]()
, k) = t(0.9,5) = 2,015 (z tabeli)
δB =0,07832
δBp = δB t(β,k) =0,07832 x 2,015 = 0,15781
H=0,156 [m]
Δh=0,001 [m]
B=2,72946
ΔBp=0,15781
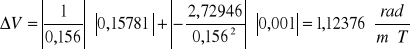
Ostateczna wartość stałej Verdeta wynosi:
![]()
Wyznaczony przez nas stosunek ![]()
także obarczony jest błędami, które wynikają z niedokładności obliczenia stałej Verdeta oraz błędu odczyty współczynnika ![]()
,

Dane:
λ=589,3x10-9 [m]
c=3x108 [m/s]
![]()
![]()
![]()
W celu wyznaczenia błędu zmiany współczynnika załamania światła względem długości fali ![]()
należy skorzystać z różniczki zupełnej:

Z wykresu odczytuję:
Δλ1= Δλ2=10 [nm]=10x10-9
Δn1= Δn2=0,001
λ 1=689,3 [nm]
n1=1,613
λ 2=489,3 [nm]
n2=1,6315
zatem:
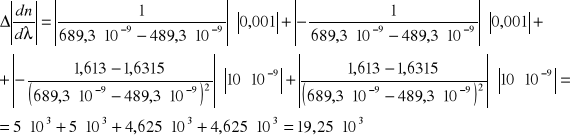
Wartość błędu ![]()
:
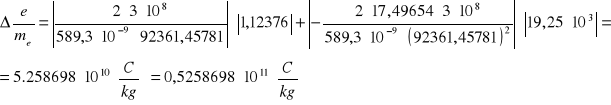
Ostateczna wartość stosunku ładunku elektronu do jego masy ![]()
wynosi:
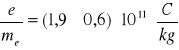
Wyszukiwarka
Podobne podstrony:
sprawko z osadów, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organic
sprawko cw1, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organiczna
Sprawko 48-fiza, Studia, II rok, fizyka
sprawko z kompleksy I, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie or
sprawko 34, Studia, II rok, fizyka
magnetyzm-nasze sprawko;), Studia, II rok, Fizyka Eksperymentalna
sprawko ohm, Studia, II rok, Fizyka Eksperymentalna
sprawko fiza 44, EIT, II rok, Fizyka lab
sprawko cw1 wersja 2, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie org
sprawko cw2, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organiczna
sprawko z kompleksów, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie org
Półprzewodniki ZENER SPRAWKO, PWr, Automatyka i Robotyka, II semestr, Fizyka 3.3, Laboratoria
sprawko wahadła, Studia, II rok, Fizyka Eksperymentalna
Sprawko grzesia i janka 36, Politechnika Wrocławska Energetyka, II semestr, Fizyka 2, Laborki, spraw
sprawko z redoskow, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organ
Foliogram nr 28 (II)
II 14 Fizyka ciala stalego
mmgg, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II sprawka
kationy, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organiczna
więcej podobnych podstron