§ 14. Całki niewłaściwe
Całki niewłaściwe to całki o granicach nieskończonych lub funkcji nieograniczonych.
14.1 Całki o granicach nieskończonych
Niech funkcja f będzie określona na przedziale nieskończonym ![]()
oraz całkowana w sensie Riemanna na każdym przedziale skończonym <a,A>, gdzie ![]()
Definicja: Całkę funkcji f o granicach a, +∞ nazywamy wielkość postaci: 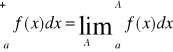
(1) gdy przy założeniu, że powyższa granica jest skończona lub nieskończona w przypadku gdy granice (1) jest skończona mówimy, że całka (1) jest zbieżna, z funkcja f całkowana na przedziale <a, ∞). Jeżeli granica (1) jest nieskończona to mówimy, że całka (1) jest rozbieżna.
Podobnie definiujemy całki:
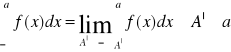
określa się też całkę 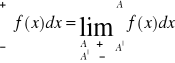
gdzie A nie zależy od A| .Twierdzenie 1 - Na to by całka 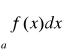
gdzie f(x)≥0 dla x≥a, była zbieżna potrzeba i wystarcza by był spełniony warunek 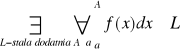
Twierdzenie 2 (kryterium porównawcze)
Jeżeli dla x≥A≥a zachodzą nierówności 0≤f(x) ≤g(x) wynika zbieżność całki 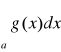
wynika zbieżność całki 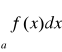
a, z rozbieżności całki
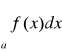
wynika rozbieżność całki 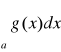
.
Dowód: Ponieważ na rozbieżność całki 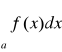
nie ma wpływu całka c więc wystarczy badać zbieżność całki 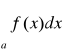
. Ponieważ dla x≥A≥a mamy 0≤f(x) ≤g(x) więc korzystając z własności całki Riemana otrzymujemy: 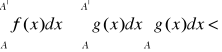
gdy ![]()
. Zatem przechodząc do granicy przy ![]()
otrzymujemy 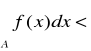
. Jeżeli założymy, że całka 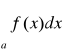
jest rozbieżna z nierówności 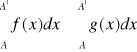
przy dowolnym ![]()
wynika, że całka 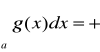
(jest rozbieżna)
Twierdzenie 3.
Jeżeli istnieje granica ![]()
dla ![]()
, g(x)>0 przy ![]()
to ze zbieżności całki 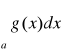
wynika zbieżność 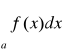
, gdy k<∞ a z rozbieżności całki
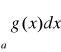
przy k>∞ wynika rozbieżność całki 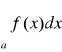
Dowód:
niech k<∞ zakładamy, że całki 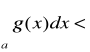
(zbieżna) Ponieważ 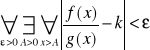
więc dla x>A mamy ![]()
=> ![]()
Stąd na podstawie twierdzenia w całka 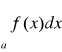
jest zbieżna niech k>0 oraz 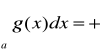
Ponieważ ![]()
więc ![]()
Podobnie jak w a. otrzymujemy oszacowanie ![]()
lub ![]()
![]()
dla x≥A| z twierdzenia 2 wynika więc rozbieżność całki
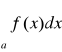
Badając zbieżność 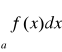
gdzie f(x)≥0 jest nieujemne dla x≥a można obrać konkretną funkcje ![]()
, która jest całkowana gdy a>0, ![]()
oraz nie jest całkowana, gdy a>0, ![]()
i stosować kryterium porównawcze.
Twierdzenie 4 (Cauchy)
Niech funkcja f ma dla dostatecznie dużych X postać ![]()
, ![]()
Wtedy:jeżeli ![]()
oraz ![]()
to całka 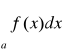
jest rozbieżna
jeżeli ![]()
oraz ![]()
to całka 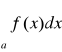
jest rozbieżna
W przypadku gdy funkcja podcałkowa zmienia znak stosujemy następujące twierdzenie 5.
Twierdzenie 5 (Cauchy)
Na to by całka 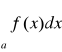
była zbieżna potrzeba i wystarcza by był spełniony warunek 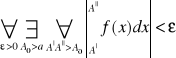
Jeżeli zbieżna jest całka 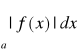
, to całka 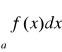
nazywa się bezwzględnie zbieżna .Z twierdzenia 5 wynika, że jeżeli zbieżna jest całka 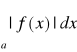
to zbieżna jest całka 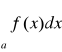
. Istnieją całki zbieżne, które nie są bezwzględnie zbieżne. np. 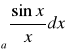
Całkę 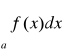
nazywamy warunkowo zbieżną gdy jest zbieżna, ale nie jest bezwzględnie zbieżna.
Twierdzenie 6. (Kryterium Abela)
Niech funkcje f,g będą określone na przedziale <a, ∞), jeżeli:
funkcja f jest całkowalna na <a, ∞)
funkcja g jest monotoniczna i ograniczona ![]()
to całka 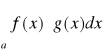
jest zbieżna
Twierdzenie 7. (Kryterium Dirichleta)
Niech funkcje f,g będą określone na przedziale <a, ∞) jeżeli
funkcja f jest całkowalna na każdym przedziale skończonym <a,A> oraz 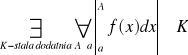
funkcja g jest ograniczona i zbieżna monotonicznie do zera przy ![]()
, to całka 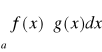
jest zbieżna
14.2 Całki niewłaściwe z funkcji nieograniczonych.
Niech funkcja f będzie ograniczona i całkowana w sensie Riemanna na każdym przedziale ![]()
gdzie ![]()
oraz nieograniczona w każdym przedziale ![]()
. Wtedy punkt b nazywamy punktem osobliwym funkcji f np. funkcje: 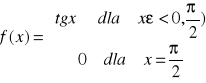
ma punkt osobliwy ![]()
. Całką funkcji f w granicach a, b a<b nazywamy wielkość
(1) 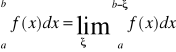
przy założeniu, że granica ta jest skończona lub nieskończona. W przypadku,, gdy granica (1) jest skończona mówimy, że całka (1) jest zbieżna, a funkcja f jest całkowalna na przedziale <a,b>
Jeżeli granica (1) jest nieskończona, to mówimy że całka (1) jest rozbieżna. Analogicznie określamy całkę 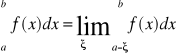
gdy funkcja ma punkt osobliwy x=a.
Ogólnie można rozważać przypadek, gdy funkcja f ma w przedziale <a,b> skończoną liczbę punktów osobliwych: c0,c1,....cn w otoczeniu których f jest nieograniczona oraz f jest ograniczona i całkowalna w każdym przedziale, który nie zawiera punktów osobliwych. Np. Dla ![]()
mamy: 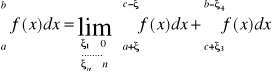
przy czym ![]()
są wzajemnie niezależne.
Podobnie jak w przypadku całek w przedziałach nieskończonych wykazujemy następujące twierdzenia. Zakładamy, że x0=b jest punktem osobliwym funkcji f.
Twierdzenie 8.
Na to by zbieżna była całka niewłaściwa (1) z funkcji nieujemnej f potrzeba i wystarcza by był spełniony warunek. 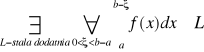
Twierdzenie 9. (Kryterium porównawcze)
Jeżeli dla ![]()
zachodzi nierówność 0≤f(x) ≤g(x) to ze zbieżności całki 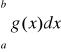
wynika zbieżności całki 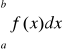
a z rozbieżności całki 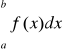
wynika rozbieżność całki 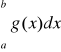
.
Przykład zbadać zbieżność całki 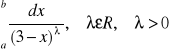
Twierdzenie 10.
Jeżeli 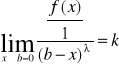
gdzie f(x)≥0 dla xε<a,b> 0≤k≤∞ to przy ![]()
gdzie 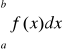
jest zbieżna, gdy k<∞ oraz całka 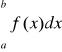
jest rozbieżna przy ![]()
oraz K>0
Twierdzenie 11. (Cauchy)
Niech funkcja f ma dla x dostatecznie ........... (granicy górnej) b postać ![]()
wtedy:
Jeżeli ![]()
oraz ![]()
to całka 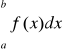
jest zbieżna
Jeżeli ![]()
oraz ![]()
to całka 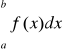
jest rozbieżna
Dla funkcji f zmieniającej znak na przedziale <a,b> stosujemy:
Twierdzenie 12. (Cauchy)
Na to by całka 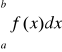
, gdzie ... jest punktem osobliwym, była zbieżna potrzeba i wystarcza by był spełniony warunek:
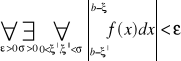
z twierdzenia 12 wynika, że jeżeli jest zbieżna całka 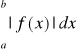
to jest zbieżna całka 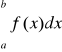
. Mówimy wtedy, że całka bezwzględnie zbieżna jest zbieżna.
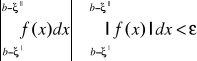
. Niech na przedziale <a,b> będzie określona funkcja f mająca dokładnie jeden punkt osobliwy ![]()
oraz całkowana w sensie Riemanna w każdym podprzedziale przedziału <a,b>, który nie zawiera punktu osobliwego c.
Wtedy 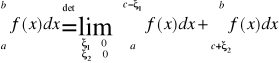
przy założeniu istnienia granicy właściwej lub niewłaściwej. Wartością główną całki niewłaściwej 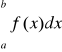
nazywamy wyrażenie 
przy założeniu istnienia granicy w sensie właściwym lub niewłaściwym. (V.p. -„Valeur pricipale”)
Mówimy wtedy, że całka 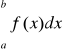
istnieje w sensie wartości głównej. Jeżeli całka 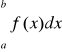
istnieje jako całka niewłaściwa to zawsze istnieje jej wartość główna. Twierdzenie odwrotne nie zachodzi.
4.3 Kryterium całkowania zbieżności szeregów liczbowych.
Twierdzenie 13.
Dany jest szereg liczb ![]()
niech f jest funkcją określoną na przedziale <1,∞), ciągłą, dodatnią, malejącą. Szereg ![]()
jest zbieżny wtedy i tylko wtedy gdy zbieżna jest całka niewłaściwa 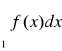
Dowód: Niech F będzie funkcją pierwotną funkcji f. Z twierdzenia Lagrange'a o wartości średniej wynika, że dla n=1,2,..... ![]()
Z monotoniczności f wynika, że ![]()
Z kryterium porównawczego zbieżności szeregów wynika, że szereg ![]()
jest zbieżny wtedy i tylko wtedy gdy zbieżny jest szereg ![]()
Ponieważ ![]()
![]()
![]()
Więc ![]()
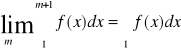
Wyszukiwarka
Podobne podstrony:
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc IV, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc II, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc I, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc III, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc III, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc VII do mdruku, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykład
Wyklady z Matematyki czesc V, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc IV, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
czesc odp zespol 2, Prywatne, Uczelnia, Budownictwo, II Semestr, Materiały Budowlane, materiały budo
Wyklady z matematyki II sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
Wyklady z matematyki IV sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
Z Wykład 15.03.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Wykład z dnia 10.05.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
Z Wykład 19.04.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Wykład 23.02.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Przykładowe egzaminy, Studia - Chemia kosmetyczna UŁ, I rok, II semestr, MATEMATYKA wykłady
Z Wykład 29.03.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
więcej podobnych podstron