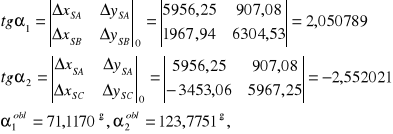Wcięcia wielokrotne
Wcięcia wielokrotne są powszechnie stosowane do zagęszczania sieci triangulacyjnych. Zagęszczanie sieci jest niezbędne do zapewnienia dogodnych nawiązań osnów poligonowych. Wcięcia wielokrotne są konstrukcjami geometrycznymi zawierającymi obserwacje nadliczbowe, założonymi przeważnie dla określenia współrzędnych pojedynczego punktu rzadziej zaś dla dwóch punktów lub ich grupy. W przypadku jednego punktu można zastosować wielokrotne wcięcia kątowe, liniowe lub kątowo-liniowe (rys.).
Wielokrotne wcięcie w przód. Wielokrotne wcięcie wstecz
Wielokrotne wcięcie kombinowane. Wielokrotne wcięcie liniowe
Obecność obserwacji nadliczbowych w konstrukcji wcięć wielokrotnych powoduje wystąpienie problemu wyrównania, które z reguły wykonywane jest metodą spostrzeżeń pośredniczących. Tok postępowania podczas tego wyrównania obejmuje następujące czynności:
1. Obliczenie przybliżonych współrzędnych ![]()
punktu wcinanego na podstawie dowolnie wybranego wcięcia pojedynczego.
2. Obliczenie wartości pomierzonych elementów konstrukcyjnych wcięcia kątów ![]()
lub długości ![]()
na podstawie współrzędnych przybliżonych.
3. Zestawienie równań błędów obserwacji kątowych lub równań błędów obserwacji liniowych.
4. Przekształcenie układu równań błędów na układ równań normalnych, który w przypadku wcięcia pojedynczego punktu składa się z dwóch równań o dwu niewiadomych.
5. Rozwiązanie układu równań normalnych, obliczenie współrzędnych punktu wcinanego, poprawek spostrzeżeń i ich wyrównanych wartości.
6. Dokonanie oceny dokładności.
Wyrównanie wcięć, w których obserwacjami kątowymi są kierunki powinno uwzględnić obecność w równaniach obserwacyjnych dodatkowej niewiadomej z zwanej niewiadomą orientującą lub stalą orientującą. Ilość niewiadomych z, występujących w danym zadaniu wyrównawczym jest równa liczbie stanowisk, na których wykonano obserwacje kierunkowe. Niewiadoma z jest azymutem (kątem kierunkowym) kreski zera podziału limbusa teodolitu ustawionego na danym stanowisku pomiarowym S, z którego dokonano pomiaru kierunków: K1, K2, K3,..., Kn. Zgodnie z poniższym rysunkiem przybliżoną wartość z, niewiadomej orientującej można określić jako różnicę azymutu ![]()
dowolnej celowej obliczonego na podstawie współrzędnych danych i przybliżonych oraz pomierzonego kierunku Ki, dla tej celowej.
Niewiadoma orientująca ![]()
W praktyce wartość przybliżoną z0 niewiadomej orientującej oblicza się najczęściej jako średnią arytmetyczną z wartości z, dla wszystkich n kierunków danego stanowiska:
![]()
Dla wartości prawdziwych: azymutu ![]()
i-tej celowej, odpowiadającego jej kierunku Ki, wychodzącego ze stanowiska S do punktu celu Pi, oraz niewiadomej orientującej z, zapiszemy funkcję:
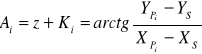
(1)
Przechodząc we wzorze (1) do wartości obserwowanych napiszemy ogólnie:
![]()
![]()
gdzie: ![]()
- przybliżona wartość azymutu (ze współrzędnych przybliżonych).
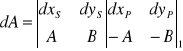
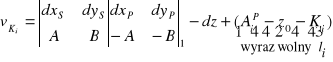
W równaniach błędów spostrzeżeń kierunkowych oprócz poprawek współrzędnych dx, dy punktów wyznaczanych wystąpi także poprawka dz niewiadomej orientującej stanowiska S.
W konstrukcji wcięcia wstecz jedynym punktem szukanym, dostarczającym dwu niewiadomych: dx, dy jest stanowisko S, natomiast punkty celu są punktami znanymi, toteż dla wyrównania wielokrotnego wcięcia wstecz równanie poprawki obserwacji kierunkowej przyjmie prostszą postać:
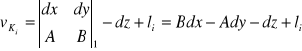
(2)
Wyrazy A, B są współczynnikami kierunkowymi celowych wstecz, obliczonymi na podstawie wzorów :
![]()
,![]()
W ramach kontroli ułożenia równań błędów sprawdzamy czy znak współczynnika przy niewiadomej dx jest zgodny ze znakiem przyrostu ![]()
, zaś znak współczynnika przy dy powinien być przeciwny do znaku ![]()
.
Do równań błędów ułożonych według formuły (2) można zastosować typową procedurę wyrównania spostrzeżeń pośredniczących, wprowadzającą niewiadomą dz wraz z pozostałymi niewiadomymi do równań normalnych. Drugi sposób wyrównania polega na stosunkowo łatwym, dzięki zależności (3), wyeliminowaniu tej niewiadomej już na etapie równań błędów, ponieważ poprawki kierunków vK tylko wtedy spełnią podstawowy warunek wyrównania [vK vK] = minimum, gdy:
![]()
(3)
Po zsumowaniu stronami n równań błędów układu otrzymamy:
![]()
tzn. poprawkę niewiadomej orientującej:
![]()
Po uwzględnieniu dz w równaniach (2), otrzymamy:
![]()
.
gdzie: ![]()
.
Współczynnik A', B' nazywamy zredukowanymi współczynnikami równań poprawek, a element L' zredukowanym wyrazem wolnym. Kontrolą obliczenia elementów zredukowanych jest zerowanie się sum:
![]()
Po zestawieniu równań normalnych na podstawie elementów zredukowanych, przeprowadzamy ich rozwiązanie, które dostarcza poprawek niewiadomych dx, dy. W dalszym ciągu realizujemy typową procedurę wyrównania spostrzeżeń pośredniczących, którą pokażemy na zamieszczonym niżej przykładzie wyrównania wielokrotnego, kierunkowego wcięcia wstecz.
Przykład: Obliczyć współrzędne punktu 6 na podstawie wyrównania wielokrotnego, kierunkowego wcięcia wstecz. Dane:
Stanowisko |
Cel |
Kierunek [grady] |
Współrzędne |
|
|
|
|
X |
Y |
6 |
1 |
0,0000 |
19557,61 |
18 524,23 |
|
2 |
71,1170 |
15 569,30 |
23 921,68 |
|
3 |
123,7750 |
10 148.30 |
23 584.40 |
|
4 |
188,4730 |
9 626,28 |
17 736,07 |
|
5 |
290,7960 |
13 652,55 |
9 822,40 |
Rozwiązanie: '
Obliczenie współrzędnych przybliżonych punktu wcinanego na podstawie pojedynczego wcięcia wstecz:
Obliczenie współczynników wagowych, ocena dokładności: Q11 = 0,000052 ; Q12= 0,000002 ; Q22= 0,000026
|
Forma rachunkowa wcięcia wstecz z punktu 6 |
|||||||||||
|
|
-3988,31 |
|
+5397,45 |
|
-9409,31 |
|
+5397,45 |
||||
|
|
+0,487618 |
+1 |
+1 |
|
+0,391845 |
-1 |
-1 |
||||
|
|
-6620,20 |
|
+3452,68 |
|
-5956,25 |
|
-907,08 |
||||
|
|
-0,15229 |
+1 |
+1 |
|
13601,36 |
|
17617,15 |
||||
Ozn. pkt |
X |
Y |
Kąty |
|
|
|||||||
|
|
|
|
g |
c |
cc |
|
|
||||
A(1) |
19557,61 |
18524,23 |
|
71 |
11 |
70 |
|
|
||||
B(2) |
15569,30 |
23921,68 |
|
123 |
77 |
50 |
|
|
||||
C(3) |
10148,30 |
23584,40 |
|
|
|
|
||||||
![]()
, ![]()
2. Obliczenie przybliżonej wartości z0 niewiadomej orientacyjnej, kierunków przybliżonych i wyrazów wolnych równań błędów:
Stanowisko |
Cel |
Kierunki pomierzone Ki |
Azymuty przybliżone
|
Stała orientująca
|
Kierunki przybliżone
|
Wyrazy wolne
|
|
1 |
0,0000 |
9,6212 |
9,6212 |
-0,0005 |
-5CC |
|
2 |
71,1170 |
80,7382 |
9,6212 |
71,1165 |
-5CC |
6 |
3 |
123,7750 |
133,3962 |
9,6212 |
123,7745 |
-5CC |
|
4 |
188,4730 |
198,0960 |
9,6230 |
188,4443 |
13CC |
|
5 |
290,7960 |
300,4181 |
9,6221 |
290,8664 |
4CC |
|
|
|
|
|
|
|
Obliczenie współczynników kierunkowych: A, B oraz współczynników zredukowanych: A', B', L':
Bok |
Przyrosty |
Współczynniki kierunkowe |
Wyraz wolny |
Współczynniki zredukowane |
||||
|
|
|
B |
A |
l |
B' |
-A' |
L' |
6-1 |
5956,25 |
907,08 |
15,9 |
104,5 |
-5 |
-6,3 |
-119,0 |
-5,4 |
6-2 |
1967,94 |
6304,53 |
92,0 |
28,7 |
-5 |
69,8 |
-43,2 |
-5,4 |
6-3 |
-3453,06 |
5967,25 |
79,9 |
-46,2 |
-5 |
57,7 |
31,7 |
-5,4 |
6-4 |
-3975,08 |
118,92 |
4,8 |
-160,0 |
13 |
-17,4 |
145,5 |
12,6 |
6-5 |
51,19 |
-7794,75 |
-81,7 |
0,5 |
4 |
-103,9 |
-15,0 |
3,6 |
|
X |
X |
111,0 22,2 |
-72,5 -14,5 |
2 0,4 |
0,0 X |
0,0 X |
0,0 X |
4. Obliczenie współczynników i zestawienie równań normalnych:
5. Wyznaczenie niewiadomych z układu równań normalnych:
6. Obliczenie poprawek i kierunków wyrównanych, kontrola ogólna:
Cel |
Kierunek A' |
B'dx |
-A'dy |
L' |
v |
K+v |
1 |
0,0000 |
-0,377 |
7,428 |
-5,4 |
1,651 |
0,00017 |
2 |
71,1170 |
4,189 |
2,699 |
-5,4 |
1,488 |
71,11715 |
3 |
123,7750 |
3,463 |
-1,982 |
-5,4 |
-3,918 |
123,77461 |
4 |
188,4730 |
-1,044 |
-9,084 |
12,6 |
2,472 |
188,47325 |
5 |
290,7960 |
-6,231 |
0,939 |
3,6 |
-1,692 |
290,79583 |
Suma |
X |
X |
X |
0,0 |
0,001 |
X |
![]()
![]()
Uwaga: Oprócz współrzędnych punktu wcinanego trzecią niewiadomą jest stała orientująca z
![]()
Stanowiska swobodne
Szczególny rodzaj wcięć przedstawiają tzw. stanowiska swobodne, które obecnie są często wykorzystywane do uzupełniania osnowy pomiarowej podczas pomiaru szczegółów metodą biegunową przy użyciu instrumentów typu total station. Stanowisko swobodne jest dogodnie usytuowanym, niestabilizowanym punktem ustawienia tachimetru elektronicznego. Położenie tego stanowiska można wyznaczać kątowym wcięciem wstecz (gdy na punktach znanych nie można ustawić pryzmatu) lub wcięciem kątowo-liniowym, dokonując pomiaru kątów poziomych lub kierunków oraz odległości do co najmniej dwóch widocznych punktów o znanych współrzędnych. Najprostszymi konstrukcjami wykorzystywanymi do określenia współrzędnych prostokątnych stanowiska swobodnego i dostarczającymi minimum niezbędnych obserwacji, są wcięcia pojedyncze. Każde dalsze zwiększenie liczby obserwacji kątowych lub liniowych, wiążących stanowisko swobodne z punktami o znanych współrzędnych (rys.), dostarcza obserwacji nadliczbowych, stwarzając tym samym problem wyrównania oraz możliwość dokonania oceny dokładności poprzez obliczenie średniego błędu położenia punktu.
Przykłady wcięć wyznaczających stanowiska swobodne
Obliczenie i wyrównanie stanowisk swobodnych
Wcięcia zawierające kąty i długości w ilości nadliczbowej wyrównujemy metodą pośredniczącą jako sieci kątowo-liniowe, przy zastosowaniu postępowania pokazanego na przykładzie kątowo-liniowego wcięcia wstecz do trzech punktów znanych (rys. b), zawierającego trzy spostrzeżenia nadliczbowe.
Przykład: Wyniki pomiaru i ich błędy:
![]()
, ![]()
, ![]()
dA = 711,50 m; dB = 569,40 m; dc = 421,10 m; md = ±0,02 m
Współrzędne punktów znanych: XA = 5000,00 , YA = 4000,00 ; XB = 4754,51 , YB = 4845,49 ; XC = 4000,00 ,
YC =4500,00.
1. Obliczenie współrzędnych przybliżonych stanowiska swobodnego na podstawie pojedynczego wcięcia wstecz:
Obliczenie współrzędnych przybliżonych umożliwia w dalszym toku postępowania zastąpienie niewiadomych współrzędnych stanowiska ![]()
, ![]()
swobodnego poprawkami ![]()
, (lub krócej: dx, dy), spełniającymi zależności:
![]()
2.. Obliczenie przybliżonych długości boków St-A, St-B, St-C i współczynników kierunkowych odległości na podstawie współrzędnych przybliżonych:
Punkty |
Odległość
|
Odległość
|
[m] |
Azymut (grady) |
sin A |
cos A |
|
od |
do |
|
|
|
|
|
|
St |
A |
711,535 |
711,500 |
+0,035 |
362,6393 |
-0,554 |
0,833 |
St |
B |
569,418 |
569,400 |
+0,018 |
58,2834 |
0,793 |
0,609 |
St |
C |
421,073 |
421,100 |
-0,027 |
183,8015 |
0,252 |
-0,968 |
3. Obliczenie kątów ![]()
podstawie współrzędnych przybliżonych:
Punkty |
Kąt przybl. (grady) |
Kąt obs. (grady) |
|
|||
Centralny |
Lewy |
Prawy |
|
|
|
|
St |
A |
B |
|
95,64407 |
95,64410 |
-0,3 |
St |
B |
C |
|
125,51806 |
125,51800 |
+0,6 |
4. Obliczenie współczynników kierunkowych obserwacji kątowych oraz zestawienie równań błędów obserwacji kątowych i liniowych Wzory:
![]()
; ![]()
Bok |
Współczynniki kierunkowe |
|
od - do |
A |
B |
St-A |
745,0 |
-495,4 |
St-B |
681,3 |
886,4 |
St-C |
-1463,2 |
380,6 |
Równania poprawek spostrzeżeń rzeczywistych:
W tym samym zadaniu występują wielkości niejednorodne tj. kąty i długości, wyrażone w różnych jednostkach. Zachodzi więc potrzeba zrównoważenia równań błędów poprzez ich obustronne podzielenie przez błędy średnie poszczególnych spostrzeżeń:
5. Po podzieleniu równań błędów przez średnie błędy spostrzeżeń otrzymujemy zrównoważony układ równań błędów, czyli równania poprawek spostrzeżeń zrównoważonych:
Nr |
a |
b |
l |
s |
1 |
+69,09 |
+3,19 |
-0,02 |
+72,26 |
2 |
-25,29 |
+107,23 |
+0,03 |
+81,97 |
3 |
-41,63 |
+27,69 |
+ 1,77 |
-12,17 |
4 |
-30,47 |
-39,65 |
+0,92 |
-69,20 |
5 |
+48,39 |
-12,58 |
-1,33 |
+34,48 |
|
20,09 |
+85,88 |
+ 1,37 |
+ 107,34 |
6. Zestawienie równań normalnych wg postępowania dla spostrzeżeń pośredniczących, jednakowo dokładnych:
Ozn. |
a] |
b] |
l] |
s] |
[a |
10417,29 |
-3045,95 |
-168,06 |
7203,28 |
[b |
-3045,95 |
14004,35 |
32,56 |
11023,52 |
[l |
-168,06 |
32,56 |
5,75 |
-129,75 |
[s |
7203,28 |
11023,52 |
-129,75 |
18097.05 |
7. Rozwiązanie równań normalnych, obliczenie współczynników wagowych: dX = +0,016 m; dY = +0,001 m XST = 4407,532 m; YST =4394,013 m
8. Obliczenie poprawek spostrzeżeń zrównoważonych i spostrzeżeń rzeczywistych, spostrzeżenia wyrównane:
Poprawki V |
Poprawki v |
|
1,1292 |
22,5843 |
95,646g |
-0,2538 |
-5,0761 |
125,5175 g |
1,1222 |
0,022444 |
711,522 m |
0,3629 |
0,007259 |
569,407 m |
-0,5510 |
-0,01102 |
421,089 m |
Poprawki rzeczywiste v otrzymujemy w wyniku pomnożenia poprawek zrównoważonych V przez odpowiednie błędy średnie spostrzeżeń rzeczywistych.
9. Kontrola ostateczna polegająca na sprawdzeniu spełnienia równań obserwacyjnych, czyli równości spostrzeżeń wyrównanych (![]()
) i spostrzeżeń określonych na podstawie współrzędnych punktów znanych i współrzędnych wyrównanych obliczonych jako niewiadome.
Obserwacja ze współrzędnych |
Obserwacja wyrównana |
95,64649 |
95,64639 |
125,51759 |
725,51759 |
711,522 m |
711,522 m |
569,407 m |
569,407 m |
421,089 m |
421,089 m |
10. Ocena dokładności:
![]()
![]()
Wyznaczenie grupy punktów
Siatka do wyznaczenia grupy punktów
Konstrukcja pokazana na rysunku nie zawiera obserwacji nadliczbowych ponieważ n = 8; u = 8), a zatem w myśl przepisów instrukcji G-2 nie powinna być stosowana do zagęszczania osnowy poziomej. Możliwe jest jednak jej wykorzystanie do rachunku współrzędnych przybliżonych poprzedzającego wyrównanie spostrzeżeń pośredniczących. Rachunek zadania rozpoczynamy od wyznaczenia kąta![]()
ze współrzędnych punktów: A, B, C, a potem, podobnie jak w zadaniu Hansena, można wykonać obliczenie wartości kątów pomocniczych: ![]()
, ![]()
. Po ich określeniu obliczamy azymuty boków: AP1, P1P2, P2P3, P3P4, P4C a następnie współrzędne punktów wyznaczanych.
1
St
A
B
C
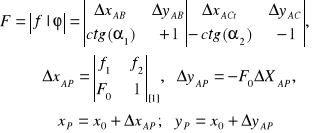
α2
α1
Wyszukiwarka
Podobne podstrony:
Wcięcia, Geodezja i Kartografia, Rachunek Wyrównawczy
Z Obliczenia dla sieci kątowej, Geodezja i Kartografia, Rachunek Wyrównawczy
Sieci płaskie, Geodezja i Kartografia, Rachunek Wyrównawczy
Obliczenia na liczbach przybliżonych, Geodezja i Kartografia, Rachunek Wyrównawczy
Ćw. 1 Zastosowanie form rachunkowych Hausbrandta, Geodezja i Kartografia, Rachunek Wyrównawczy
S 7 Równania obserwacji 3, Geodezja i Kartografia, Rachunek Wyrównawczy
Wyrównanie parametryczne - metoda macierzowa, Geodezja i Kartografia, Rachunek Wyrównawczy
Wagi i błędności, Geodezja i Kartografia, Rachunek Wyrównawczy
Wyrównania korelat, Geodezja i Kartografia, Rachunek Wyrównawczy
Ściaga RW, Geodezja i Kartografia, Rachunek Wyrównawczy
Z Wyrównanie obserwacji bezpośrednich, Geodezja i Kartografia, Rachunek Wyrównawczy
Równania ogólne poprawek, Geodezja i Kartografia, Rachunek Wyrównawczy
S 6 Spostrzeżenia niejednakowo dokładne, Geodezja i Kartografia, Rachunek Wyrównawczy
S 6 Spostrzeżenia bezpośrednie, Geodezja i Kartografia, Rachunek Wyrównawczy
Miary dokładności spostrzeżeń, Geodezja i Kartografia, Rachunek Wyrównawczy
S 5 Błedy wstęp, Geodezja i Kartografia, Rachunek Wyrównawczy
Sieci wysokościowe regionalne, Geodezja i Kartografia, Rachunek Wyrównawczy
więcej podobnych podstron