Nr ćwiczenia: 5	Temat ćwiczenia: Badanie zależności mocy użytecznej od obciążenia	Ocena z teorii:
Nr zespołu: 2	Imię i nazwisko: XXX	Ocena zaliczenia ćwiczenia:
Data: 05.04.2013	Wydział IEiT, rok I, grupa 4	Uwagi:

Wtęp teoretyczny:

Potencjał i napięcie elektryczne

Potencjał elektryczny - pole skalarne opisujące pole elektryczne. Potencjałem elektrycznym w dowolnym punkcie pola elektrycznego nazywa się stosunek pracy wykonanej przez siłę elektryczną (przy przenoszeniu ładunku q z tego punktu do nieskończoności), do wartości tego ładunku.

(1)

Napięcie elektryczne - różnica potencjałów elektrycznych między dwoma punktami obwodu elektrycznego lub pola elektrycznego. Symbolem napięcia jest U. Napięcie elektryczne jest to stosunek pracy wykonanej podczas przenoszenia ładunku elektrycznego między punktami, dla których określa się napięcie, do wartości tego ładunku.

(2)

Siła elektromotoryczna

Czynnik powodujący przepływ prądu w obwodzie elektrycznym równy energii elektrycznej zyskanej przez jednostkowy ładunek przemieszczany w źródle prądu elektrycznego w przeciwnym kierunku do sił pola elektrycznego oddziałującego na ten ładunek. Siła elektromotoryczna źródła jest zdefiniowana jako iloraz pracy wykonanej przez źródło do wartości przenoszonego ładunku. Siła elektromotoryczna w obwodzie z prądem jest równa stosunkowi mocy elektrycznej wydzielanej w obwodzie do natężenia prądu.

(3)

Natężenie pradu elektrycznego

Natężenie prądu (nazywane potocznie prądem elektrycznym) jest wielkością fizyczną charakteryzującą przepływ prądu elektrycznego zdefiniowaną jako stosunek wartości ładunku

elektrycznego przepływającego przez wyznaczoną powierzchnię do czasu przepływu ładunku.

(4)

Opór elektryczny

Wielkość charakteryzująca relacje między napięciem a natężeniem prądu elektrycznego w obwodach prądu stałego. W obwodach prądu przemiennego rezystancją nazywa się część rzeczywistą zespolonej impedancji.

Prawo Ohma

Prawo fizyki głoszące proporcjonalność natężenia prądu płynącego przez przewodnik do napięcia panującego między końcami przewodnika. Dla prądu stałego proporcjonalność napięcia U i prądu I wyraża się wzorem:

(5)

Prawa Kirchhoffa

I. Prądowe: Suma natężeń prądów wpływających do węzła jest równa sumie natężeń prądów wypływających z tego węzła.

II. Napięciowe: W zamkniętym obwodzie suma spadków napięć na oporach równa jest sumie sił elektromotorycznych występujących w tym obwodzie.

Moc prądu

Moc urządzeń elektrycznych wyraża się iloczynem natężenia przepływającego przez nie prądu I i napięcia elektrycznego U, do którego urządzenie jest włączone. Moc użyteczna jest to moc zużyta na wykonanie określonego zadania z pominięciem mocy wydzielonej na rezystancjach.

(6)

Dopasowanie obciążenia zasilacza

Dopasowanie energetyczne obciążenia do źródła jest to zapewnienie warunków pozwalających na przekazanie maksymalnej mocy ze źródła do obciążenia. W obwodach prądu stałego warunek ten to równość rezystancji obciążenia z rezystancją wewnętrzną źródła: R_ob = R_wźr

Sprawność

Skalarna bezwymiarowa wielkość fizyczna określająca w jakim stopniu urządzenie, lub proces przekształca energię występującą w jednej postaci w energię w innej postaci.

(7)

Sprawność wyrażana jest w jednostkach względnych jako ułamek, często w zapisie procentowym. Z zasady zachowania energii wynika, że sprawność nie może być większa od jedności czyli od 100%.

Celem ćwiczenia było wyznaczenie mocy użytecznej oraz oporności wewnętrznej źródła na podstawie pomiaru prądu w obwodzie i napięcia na oporności obciążenia w zależności od wartości tej oporności. Doświadczenie przeprowadzono przy stanowisku wyposażonym w woltomierz, amperomierz, regulowany opornik i zasilacz zestawione w sposób przedstawiony na ponższym schemacie. Mierniki ustawiono na tryb pracy z prądem i napięciem stałym. 

Schemat 1

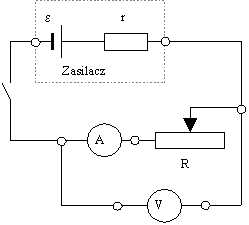
Ad 1. Posługując się pokrętłem na oporniku zmieniano wartość rezystancji oraz notowano zmiany prądu i napięcia. Na ich podstawie obliczono opór obciążenia (wzór (5)) oraz moc wydzieloną na obciążeniu (Pu=U·I)). Zgromadzone dane umieszczono w tabeli 1.

Ad 3. Wykres 1 przedstawia zależność U=f(I). Z wykresu tego można wyznaczyć wartości siły elektromotorycznej ε oraz oporności wewnętrznej r jako współczynniki równania prostej: y =-ax+b. Odpowiednio a=r , b=ε .Wynoszą one:

a≈2,918 b≈3,038 r =291,8 Ω ε=3,04 V

Wykres 1 (Ad 2.)

Tabela 1

U [V]	I [mA]	R[Ω]	P[mW]	PumW]	η	R/r
2,76	1,28	2156,25	3,89	3,53	90,79%	7,39
2,75	1,32	2083,33	4,01	3,63	90,46%	7,14
2,73	1,39	1964,03	4,23	3,79	89,80%	6,73
2,72	1,45	1875,86	4,41	3,94	89,47%	6,43
2,71	1,5	1806,67	4,56	4,07	89,14%	6,19
2,69	1,6	1681,25	4,86	4,30	88,49%	5,76
2,67	1,68	1589,29	5,11	4,49	87,83%	5,45
2,65	1,75	1514,29	5,32	4,64	87,17%	5,19
2,64	1,83	1442,62	5,56	4,83	86,84%	4,94
2,62	1,89	1386,24	5,75	4,95	86,18%	4,75
2,60	1,97	1319,80	5,99	5,12	85,53%	4,52
2,59	2,06	1257,28	6,26	5,34	85,20%	4,31
2,55	2,22	1148,65	6,75	5,66	83,88%	3,94
2,50	2,44	1024,59	7,42	6,10	82,24%	3,51
2,45	2,67	917,60	8,12	6,54	80,59%	3,14
2,40	2,9	827,59	8,82	6,96	78,95%	2,84
2,35	3,14	748,41	9,55	7,38	77,30%	2,56
2,30	3,35	686,57	10,18	7,71	75,66%	2,35
2,25	3,57	630,25	10,85	8,03	74,01%	2,16
2,20	3,82	575,92	11,61	8,40	72,37%	1,97
2,15	4,04	532,18	12,28	8,69	70,72%	1,82
2,10	4,26	492,96	12,95	8,95	69,08%	1,69
2,05	4,5	455,56	13,68	9,23	67,43%	1,56
2,00	4,71	424,63	14,32	9,42	65,79%	1,46
1,95	4,96	393,15	15,08	9,67	64,14%	1,35
1,90	5,17	367,50	15,72	9,82	62,50%	1,26
1,85	5,41	341,96	16,45	10,01	60,86%	1,17
1,80	5,64	319,15	17,15	10,15	59,21%	1,09
1,75	5,85	299,15	17,78	10,24	57,57%	1,03
1,70	6,1	278,69	18,54	10,37	55,92%	0,96
1,65	6,31	261,49	19,18	10,41	54,28%	0,90
1,60	6,55	244,27	19,91	10,48	52,63%	0,84
1,55	6,79	228,28	20,64	10,52	50,99%	0,78
1,50	6,99	214,59	21,25	10,49	49,34%	0,74
1,45	7,21	201,11	21,92	10,45	47,70%	0,69
1,40	7,48	187,17	22,74	10,47	46,05%	0,64
1,35	7,67	176,01	23,32	10,35	44,41%	0,60
1,30	7,89	164,77	23,99	10,26	42,76%	0,56
1,25	8,12	153,94	24,68	10,15	41,12%	0,53
1,20	8,38	143,20	25,48	10,06	39,47%	0,49
1,15	8,6	133,72	26,14	9,89	37,83%	0,46
1,10	8,83	124,58	26,84	9,71	36,18%	0,43
1,05	9,02	116,41	27,42	9,47	34,54%	0,40
1,00	9,27	107,87	28,18	9,27	32,89%	0,37
0,95	9,5	100,00	28,88	9,03	31,25%	0,34
0,90	9,75	92,31	29,64	8,78	29,61%	0,32
0,85	9,97	85,26	30,31	8,47	27,96%	0,29
0,80	10,16	78,74	30,89	8,13	26,32%	0,27
0,75	10,42	71,98	31,68	7,82	24,67%	0,25
0,70	10,64	65,79	32,35	7,45	23,03%	0,23
0,65	10,86	59,85	33,01	7,06	21,38%	0,21
0,61	11,05	55,20	33,59	6,74	20,07%	0,19
0,55	11,3	48,67	34,35	6,22	18,09%	0,17
0,50	11,56	43,25	35,14	5,78	16,45%	0,15
0,44	11,82	37,23	35,93	5,20	14,47%	0,13
0,40	12,02	33,28	36,54	4,81	13,16%	0,11
0,31	12,42	24,96	37,76	3,85	10,20%	0,09
0,26	12,61	20,62	38,33	3,28	8,55%	0,07
0,20	12,91	15,49	39,25	2,58	6,58%	0,05
0,15	13,14	11,42	39,95	1,97	4,93%	0,04

Ad 4. Korzystając z metody najmniejszych kwadratów obliczono niepewności pomiaru współczynników. Wynoszą one:

Δr ≈ ±0,01 Ω

Δε ≈ ±0,0008 V

Obliczenia wykonano przy pomocy programu Excel 2003.

Ad 5. Mając określone natężenie prądu i wartość siły elektromotorycznej obliczono moc całkowitą (P=ε·I). Otrzymane wyniki umieszczono w tabeli 1.

Sprawność obliczono jako stosunek mocy wydzielonej na rezystancji do mocy całkowitej. Uzyskane dane umeszczono w tabeli 1 i przedstawiono na wykresie 2.

Wykres 2.

Ad 5. Poniższe wykresy przedstawiają moc całkowitą (3) oraz moc użyteczną (4) w funkcji stosunku oporności obciążenia do oporności wewnętrznej R/r.

Wykres 3.

Wykres 4.

Moc użyteczna osiąga najwyższą wartośc dla R/r≈1. Jest to zgodne z zasadą dopasowania, która mówi, że gdy rezystancja wewnętrzna i zewnętrzna mają taką samą wartość, to moc na rezystancji zewnętrznej jest maksymalna. W badanym przykładzie sprawność wynosi wtedy około 56%.

Wnioski

Na wykresie mocy całkowitej w funkcji R/r, można zauważyć, że jest ona niewielka dla dużych wartości rezystancji zewnętrznej. Jest to spowodowane tym, że przy tak dużych wartościach rezystancji prąd płynący przez opornik jest bardzo mały.

Z wykresu sprawności w funkcji R/r można wywnioskować, iż sprawność jest tym większa, im większa jest wartość oporu zewnętrznego. Jest to spowodowane tym, że wraz ze wzrostem oporu, zwiększa się wartość napięcia odkładanego na oporniku.

- 6 -

---