
Politechnika Śląska
Wydział Inżynierii Materiałowej
i Metalurgii
LABOLATORIUM Z FIZYKI
TEMAT ĆWICZENIA nr 4 : Pomiar czasu zderzenia kul i wyznaczenie parametrów deformacji.
Grupa: ZIP 22 sekcja:2
Rok akademicki: 2012/2013
Uwagi prowadzącego nr1:
Uwagi prowadzącego nr2:
Uwagi prowadzącego nr 3 :
|
||
Data przyjęcia |
Ocena końcowa
|
Podpis prowadzącego |
1)Przebieg ćwiczenia:
Złożyć układ pomiarowy według schematu . Kulki zawieszone są na cienkich przewodach umocowanych do obudowy. Układ posiada dwa elektromagnesy służące do utrzymywania kul w położeniu odchylonym od pionu o kąt
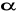
.Zmierzyć odległości kul od podstawy, gdy kule zwisają swobodnie. Zanotować pojemność kondensatora C i średnicę kul d=3,18cm.
Włączyć zasilacz i ustawić napięcie 27V. Odchylić kulki tak, aby dotknęły elektromagnesów i zmierzyć ich odległość od podstawy.
Naładować kondensator poprzez włączenie na kilka sekund wyłącznika W
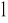
i zanotować napięcie U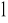
, jakie wskazuje woltomierz.Naciskając na chwilę wyłącznik W
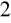
zwolnić kule. Po zderzeniu powinny one zostać przyciągnięte przez elektromagnesy. Zanotować napięcie U w chwilę po zetknięciu..Pomiary opisane w punkcie 4 i 5 powtórzyć dla 11 wartości od 0
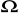
do 10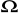
, zmieniając opór co jeden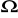
.
2) Opracowanie wyników:
Obliczenie wartość średnich oraz odchyleń standardowych następujących wielkości:
Lp |
1 |
2 |
3 |
4 |
5 |
Suma |
średnia |
odchylenie |
H1[cm] |
10,5 |
10,4 |
10,6 |
10,4 |
10,5 |
52,4 |
10,48 |
2,34 |
H2[cm] |
11,5 |
11,4 |
11,6 |
11,5 |
11,4 |
57,4 |
11,48 |
2,57 |
H=H1-H2 |
1 |
1 |
1 |
1,1 |
0,9 |
5 |
1 |
0,22 |
wzór na średnia:
Wzór na odchylenie: 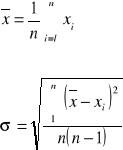
a) odległość kul od podstawy, gdy kule zwisają swobodnie
Obliczona wartość wynosi:
H1 = (0,1048±0,0234) [m]
b). odległość kul od podstawy, gdy kule dotykają elektromagnesów
Obliczona wartość wynosi:
H2 = (0,1148±0,0257) [m]
c) Różnica odległości kul.
H= (0,0010 ± 0,0002) [m]
Opór |
Uo napiecie przed zderzeniem |
napięciena kondensatorze po zderzaniu U[V]
|
suma |
średnia |
odchylenie |
||||
10 |
27 |
10,6 |
10,5 |
10,5 |
10,6 |
10,4 |
52,6 |
10,52 |
2,35 |
9 |
27 |
9,4 |
9,3 |
9,5 |
9,6 |
9,6 |
47,4 |
9,48 |
2,12 |
8 |
27 |
8,5 |
8,5 |
8,5 |
8,6 |
8,6 |
42,7 |
8,54 |
1,91 |
7 |
27 |
7,5 |
7,5 |
7,7 |
7,5 |
7,5 |
37,7 |
7,54 |
1,69 |
6 |
27 |
6,5 |
6,6 |
6,4 |
6,6 |
6,7 |
32,8 |
6,56 |
1,47 |
5 |
27 |
4,7 |
5,2 |
4,7 |
5,2 |
4,6 |
24,4 |
4,88 |
1,1 |
4 |
27 |
3,2 |
3,6 |
3,7 |
3,7 |
3,4 |
17,6 |
3,52 |
0,79 |
3 |
27 |
2,2 |
1,7 |
1,5 |
1,6 |
1,7 |
8,7 |
1,74 |
0,39 |
2 |
27 |
0,7 |
0,6 |
0,6 |
0,6 |
0,7 |
3,2 |
0,64 |
0,14 |
1 |
27 |
0,2 |
0,3 |
0,4 |
0,1 |
0,2 |
1,2 |
0,24 |
0,06 |
0 |
27 |
0,1 |
0,1 |
0 |
0 |
-0,2 |
0 |
0 |
0 |
d) Napięcie po zderzeniu kul
U1=(10,52 ± 2,35)[V]
U2=(9,48 ± 2,12)[V]
U3=(8,54 ± 1,91)[V]
U4=(7,54 ± 1,69)[V]
U5=(6,56 ± 1,47)[V]
U6=(4,88 ± 1,10)[V]
U7=(3,52 ±0,79)[V]
U8=(1,74 ± 0,39)[V]
U9=(0,64 ± 0,14)[V]
U10=(0,24 ± 0,06)[V]
U11=(0 ± 0)[V]
Sporządzenie wykresu zależności 1/ln(Uo/U) = R:
Opór [Ω] |
U0[V] |
Uśr[V] |
1/ln(Uo/U) |
10 |
27 |
10,52 |
1,06 |
9 |
27 |
9,48 |
0,96 |
8 |
27 |
8,54 |
0,87 |
7 |
27 |
7,54 |
0,78 |
6 |
27 |
6,56 |
0,71 |
5 |
27 |
4,88 |
0,58 |
4 |
27 |
3,52 |
0,49 |
3 |
27 |
1,74 |
0,36 |
2 |
27 |
0,64 |
0,27 |
1 |
27 |
0,24 |
0,21 |
0 |
27 |
0 |
0 |
Parametry prostej aproksymującej:
Obliczamy za pomocą poniższych wzorów
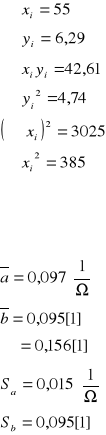

Wynik:
a=(0,097 ± 0,015) [1/Ω]
b=(0,095 ± 0,095) [1]
Obliczanie czasu rozładowania kondensatora
Pojemność kondensatora C =10 [μF]
![]()
Niepewność obliczenia czasu t:
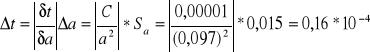
![]()
Obliczanie wielkości h ugięcia czaszy kuli
Wyznaczamy korzystając ze średniej różnicy odległości kul od podstawy podczas przymocowania do elektromagnesów i swobodnego zwisania H=0,001 [m] oraz zależności:
g = 9,81 [m/s2] - przyspieszenie grawitacyjne
![]()
Niepewność wyznaczenia wielkości ugięcia czaszy kuli:
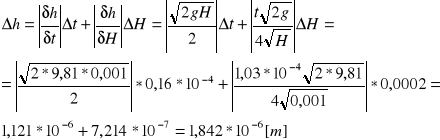
![]()
[m]
Obliczenie modułu sprężystości kuli.
Wzór do wyznaczania E jest następujący:
=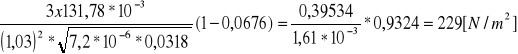
gdzie:
m = 131,78 ×10- 3 [kg] - masa kuli
= 0,26 - współczynnik Poissona dla żelaza lanego
d = 0,0318 [m] - średnica kul
t = (1,03 ± 0,16) ×10- 4 [s] - czas rozładowania kondensatora
h = (7,2 ± 1,8) ×10- 6 [m] - ugięcie czaszy kuli
Niepewność wyznaczenia E modułu sprężystości kuli.
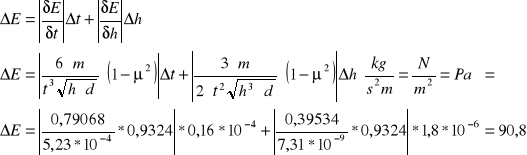
Moduł sprężystości kuli wynosi:
E = (229 ± 91) [N/m2]
7. Porównanie wyznaczonego modułu sprężystości E z wartością Et.
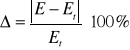
=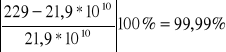
E = (229 ± 91) [N/m2] - moduł sprężystości wyznaczony doświadczalnie
Et = 21,9 ×1010 [N/m2] - wartość odczytana z tablic (dla stali)
W obliczeniach uzyskaliśmy błąd względny procentowy ∆E=99,99%.
3) Zestawienie wyników
H1 = (10,48±2,34) [cm] - odległość kul zwisających swobodnie
H2 = (11,48±2,57) [cm]- odległość kul przyciągniętych elektromagnesem
H= (1 ± 0,22) [cm] - różnice odległości kul
Wartości napięć po zderzeniu się kul
U1=(10,52 ± 2,35)[V]
U2=(9,48 ± 2,12)[V]
U3=(8,54 ± 1,91)[V]
U4=(7,54 ± 1,69)[V]
U5=(6,56 ± 1,47)[V]
U6=(4,88 ± 1,10)[V]
U7=(3,52 ±0,79)[V]
U8=(1,74 ± 0,39)[V]
U9=(0,64 ± 0,14)[V]
U10=(0,24 ± 0,06)[V]
U11=(0 ± 0)[V]
Współczynniki prostej
a=(0,097 ± 0,015) [1/Ω]
b=(0,095 ± 0,095) [1]
Czas rozładowania kondensatora:
![]()
Wielkość ugięcia czaszy:
![]()
[m]
Modułu sprężystości kuli:
E = (229 ± 91) [N/m2]
∆E=99,99%. błąd względny uzyskany z porównania obliczonego modułu sprężystości z danymi tablicowymi.
4) Wnioski
By zniwelować błędy pomiarowe obliczyliśmy średnią oraz odchylenie. Po przeanalizowaniu wyników możemy stwierdzić, że im niższy opór tym mniejsze napięcie.
Na podstawie wykresu zależności 1/ln(Uo/U) = f(R) stwierdzamy, że jest to zależność liniowa. Zależność tą aproksymowaliśmy prostą o równaniu 1/ln(Uo/U) = aR + b gdzie:
a= (0,097 ± 0,015) [1/Ω]
b= (0,095 ± 0,095) [bw]
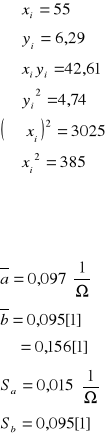
Wyszukiwarka
Podobne podstrony:
galwanometr, ZIP POLSL, Fizyka
Projekttt, ZIP POLSL
Fizyka ćw. zad, studia GIG polśl, fizyka
cwiczenie 10, PWR ZIP, lab fizyka
philips, ZIP POLSL
Sprawozdanie Ćwiczenie 44a, PWR ZIP, lab fizyka
Ćwiczenie 28, PWR ZIP, lab fizyka
Galwanometron, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Spraw
Karta pomiarowa, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fiz
sciagafizykabudowli, Studia Budownictwo polsl, III semestr KBI, Fizyka budowli, Fizyka Budowli
betabartek, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyka l
Fiza-pojecia, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyka
zadania z fizyki na kolosy, Studia POLSL, STUDIA, Fizyka, kolokwia
Pytania i odpowiedzi FCS ost, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, S
krzywebartek, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyka
widmo-1, Transport Polsl Katowice, 2 semestr, Fizyka, Fizyka Ja
Monochromator, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyk
fizykawyklad 001ukladyodniesienia, Transport Polsl Katowice, 2 semestr, Fizyka, FIZA, fizyka
więcej podobnych podstron