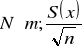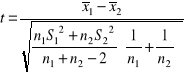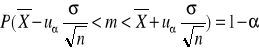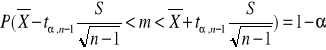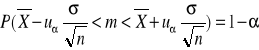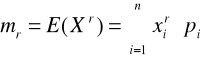
Dystrybuanta

F(x) = P(X Ⴃ x) dla x ჎ R

Moment zwykły rzędu r:

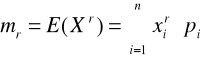
Moment centralny rzędu r:

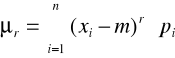
Wartość oczekiwana

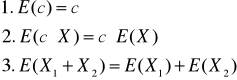
Wariancja

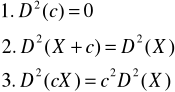
Kwartyle

Q1:

Q2:

Q3:

Współczynnik skośności:

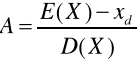
Rozkład zero-jedynkowy

E(X)= p

D2(X) = pq

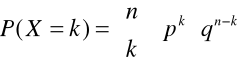
Rozkład Bernoulliego (dwumianowy)

E(X) = np

D2(X) = npq

Gęstość prawdopodobieństwa

Dystrybuanta

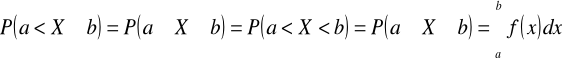
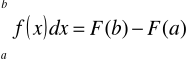
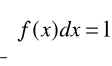
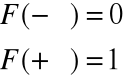
Wartość oczekiwana

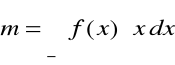
wariancja

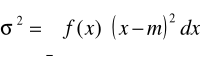
Rozkład normalny (Gaussa)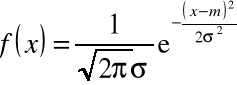

Rozkład równomierny typu ciągłego

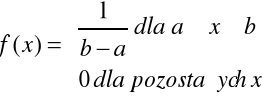
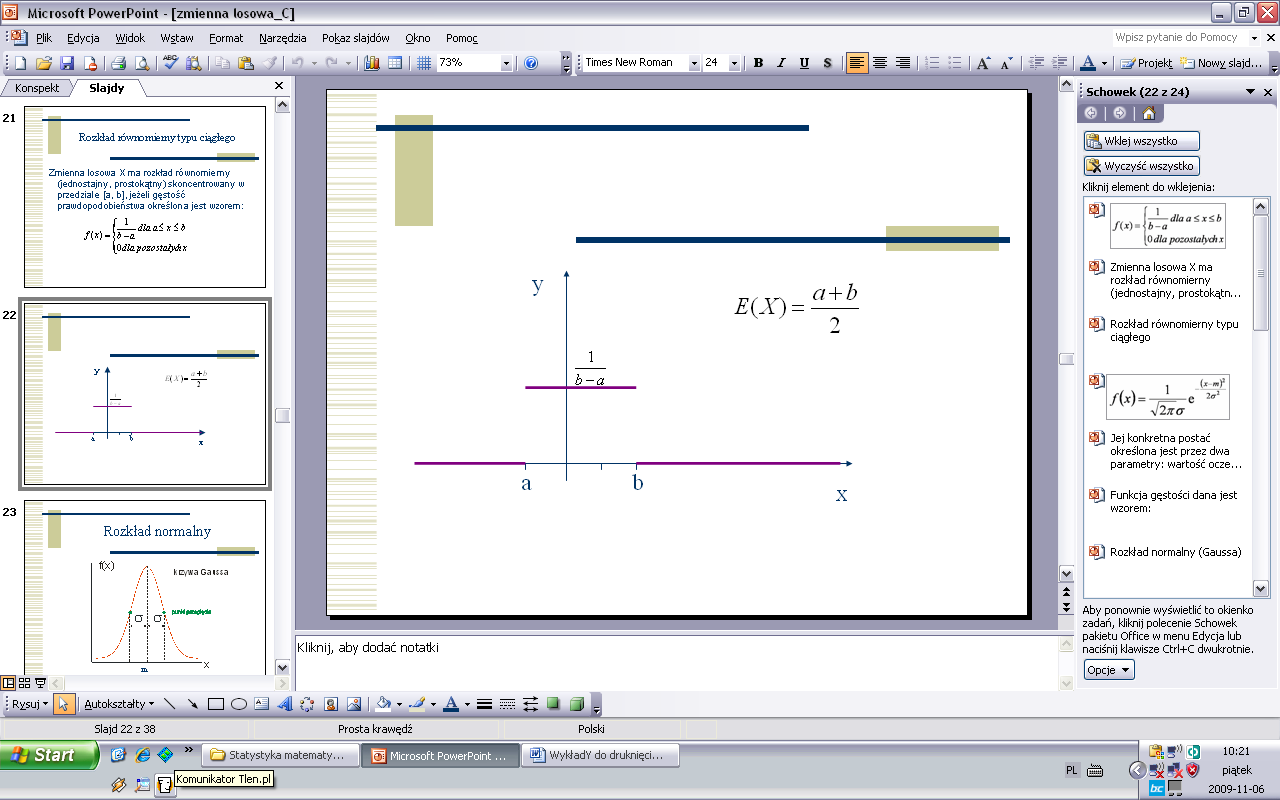
Reguła „trzech sigma”

68,3 % populacji mieści się w przedziale (ၭ - σ; ၭ + σ)

• 95,5 % populacji mieści się w przedziale (ၭ - 2σ; ၭ + 2σ)

• 99,7 % populacji mieści się w przedziale (ၭ - 3σ; ၭ + 3σ)

Standaryzacja

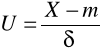
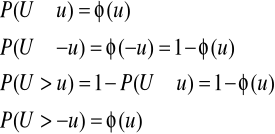
Centralne twierdzenie graniczne

Estymacja parametrów

Średnia dla próby

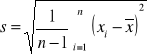
odchylenie standardowe dla próby

Przedziały ufności dla wartości oczekiwanej

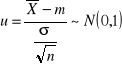
Przedział ufności dla wartości oczekiwanej, gdy znane jest odchylenie standardowe

Cecha X ma w populacji rozkład normalny N(m, σ), odchylenie standardowe σ jest znane

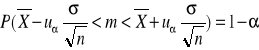
Przedział ufności dla wartości oczekiwanej, gdy odchylenie standardowe jest nieznane

Gdy próba jest mała nႣ30

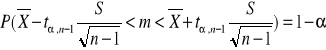
Gdy próba jest duża n>30

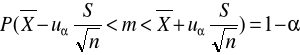
Przedział ufności dla wartości oczekiwanej, gdy nieznany jest rozkład w populacji - tylko dla dużych prób

• 
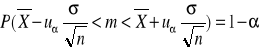
  Nieznane σ można przybliżyć obliczonym z dużej próby odchyleniem standardowym S

Przedział ufności dla prawdopodobieństwa (dla frakcji) - tylko dla n>120

Estymatorem prawdopodobieństwa p w populacji generalnej jest wskaźnik struktury (frakcja)

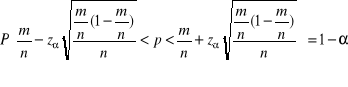
TESTY ISTOTNOŚCI DLA WARTOŚCI ŚREDNIEJ

W POPULACJI

Model pierwszy

• populacja ma rozkład normalny o nieznanym m oraz znanym

1⁰

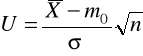
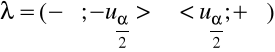
Obszar krytyczny (dwustronny)

ϕ(u)

0
u

Obszar krytyczny (prawostronny)

ϕ(u)

0 u_α u

Obszar krytyczny (lewostronny)

ϕ(u)

-u_α 0 u

Model drugi

- populacja ma rozkład normalny o nieznane m oraz nieznane ,

- mała próba (n<120).

,

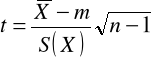
Model trzeci

- populacja ma dowolny rozkład z nieznanymi parametrami,

- duża próba (n>120).

,

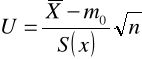
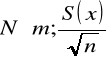
TEST ISTOTNOŚCI DLA DWÓCH ŚREDNICH

Postać H0	m1 = m2
Model pierwszy	Rozkłady normalne o znanych wariancjach
Statystyka testująca
Rozkład statystyki testującej	N(0;1)
Model drugi	Rozkłady normalne o nieznanych wariancjach małe próby (n1+n2-2≤120)
Statystyka testująca
Rozkład statystyki testującej	t-Studenta o n1+n2-2 stopniach swobody
Model trzeci	Rozkłady normalne o nieznanych wariancjach duże próby (n1+n2-2>120)
Statystyka testująca
Rozkład statystyki testującej	N(0;1)

TEST ISTOTNOŚCI DLA FRAKCJI

Postać H0	p = p0
Rozkład dwupunktowy próba duża (n>120)
Statystyka testująca
Rozkład statystyki testującej	N(0;1)

TEST ISTOTNOŚCI DLA DWÓCH FRAKCJI

Postać H0	p1 = p2
Rozkład dwupunktowy, próba duża (n1>120 oraz n2>120)
Statystyka testująca	, gdzie ,
Rozkład statystyki testującej	N(0;1)

8

---
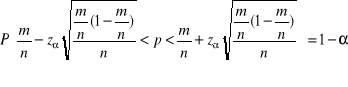
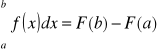
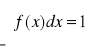
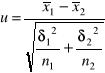
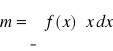
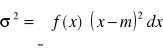
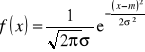
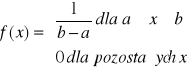
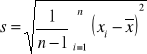
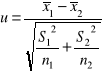
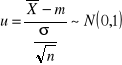