WEWNĄTRZSZKOLNY KONKURS MATEMATYCZNY

LIGA ZADANIOWA

etap 10 - odpowiedzi

Klasy I

10. Ilu tragarzy powinien wynająć i jak postępować podróżny, który chce przejść przez pustynię, jeżeli droga przez nią trwa 6 dni, każdy zaś z tragarzy i sam podróżnik mogą unieść racje żywności na 4 dni.

Odp. Podróżny wynajmuje tragarzy i w trakcie trasy zawraca ich do punktu wyjścia z taką ilością wody, by starczyła im na powrót.

Zakładam, że podróżny wynajmie:

2. 1 tragarza, który po
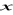
   dniach wróci do domu. Resztę podróży (czyli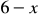
   dni) podróżny przejdzie sam.

Zużyją razem:
porcji żywności. (Wyjaśnienie na rys.)

Wyruszyli z
porcjami.

.

Czyli na resztę trasy musiał wziąć 5 porcji wody (sprzeczność)

3. 2 tragarzy, z których jeden wróci do domu po
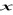
   dniach, a drugi wróci do domu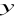
   dni później. Resztę podróży (czyli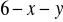
   dni) podróżny przejdzie sam.

Zużyją razem:
porcji żywności. (Wyjaśnienie na rys.)

Wyruszyli z
porcjami.

Jedynymi rozwiązaniami tego równania w zbiorze liczb naturalnych jest
i
.

Odp. Podróżnik musi zatrudnić 2 tragarzy. Po pierwszym dniu 1 tragarz wraca do domu (zabiera 1 porcję żywności ze sobą, reszta idzie dalej z 8 porcjami). Po drugim dniu 2 tragarz wraca do domu (zabiera ze sobą 2 porcje, dalej idzie podróżnik sam niosąc 4 porcje).

Klasy II

10. Liczbę naturalną
nazywamy doskonałą, jeżeli jest ona równa sumie wszystkich swoich dzielników naturalnych mniejszych od tej liczby. Liczbą doskonałą jest np. 6, bo:
. Znaleźć wszystkie liczby doskonałe postaci
, gdzie
i
są różnymi liczbami pierwszymi.

Odp. Dzielniki liczby
: 1,
,
,
,
. Z definicji liczby doskonałej otrzymujemy równanie:




.

Liczba
dzieli lewą stronę równania, więc musi dzielić i prawą, czyli
dzieli
. Zatem istnieje liczba naturalna
taka, że


.

Podstawiając to do pierwszego równania otrzymujemy:

.

Liczba
dzieli lewą stronę równania, więc musi dzielić i prawą, czyli
jest dzielnikiem
. Zatem
.

• Niech
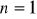
  . Wtedy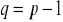
  . Liczby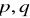
  są kolejnymi liczbami naturalnymi. Jedynymi liczbami pierwszymi, które są kolejnymi liczbami naturalnymi są 2 i 3. Stąd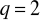
  i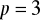
  .
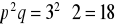
  . Sprawdzamy czy 18 jest liczbą doskonałą.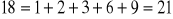
  . Sprzeczność.

• Niech
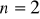
  . Wtedy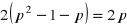
  
  
  
  
  

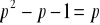
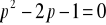
. Rozwiązaniami tego równania są
i
. Obie te liczby nie są naturalne. Sprzeczność.

• Niech
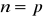
  . Wtedy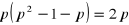
  
  
  
  
  .

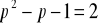
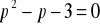
. Rozwiązaniami tego równania są
i
. Obie te liczby nie są naturalne. Sprzeczność.

• Niech
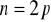
  . Wtedy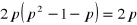
  
  
  
  
  .

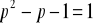
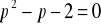
. Rozwiązaniami tego równania są
i
. Tylko
spełnia warunki zadania (2 jest liczbą pierwszą). Wtedy
i
.

Liczba
. Sprawdzamy czy 28 jest liczbą doskonałą.
.

Odp. Jedyną liczbą doskonałą postaci
, gdzie
i
są różnymi liczbami pierwszymi, jest 28.

Klasy III

10. Udowodnij, że punkt styczności okręgu wpisanego w trójkąt prostokątny z przeciwprostokątną dzieli tę przeciwprostokątną na odcinki, których iloczyn jest równy polu  tego trójkąta.

Odp. Jeżeli ramiona kąta są styczne do okręgu, to odległości wierzchołka tego kąta od punktów styczności są takie same. Stąd oznaczenia na rysunku.

Z twierdzenia Pitagorasa wynika, że:

.

Pole trójkąta:




.

Co należało udowodnić.

Zadania i rozwiązania znajdziecie na http://chomikuj.pl/matematyka4lo/Liga+zadaniowa

6 - x

x

x

6 - x - y

y

y

y

x

x

r

r

r

r

r

---